রেখা, রশ্মি ও রেখাংশ

আজকে আমাদের আলোচনার বিষয়ঃ রেখা, রশ্মি ও রেখাংশ । এটি নবম – দশম শ্রেনী গণিতের রেখা, কোণ ও ত্রিভুজ এর অন্তর্গত।

 

 

রেখা, রশ্মি ও রেখাংশ

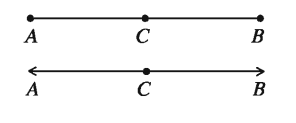
সমতলীয় জ্যামিতির স্বীকার্য অনুযায়ী সমতলে সরলরেখা বিদ্যমান যার প্রতিটি বিন্দু সমতলে অবস্থিত। মনে করি, সমতলে AB একটি সরলরেখা এবং রেখাটির উপর অবস্থিত একটি বিন্দু C। C বিন্দুকে A ও B বিন্দুর অন্তবর্তী বলা হয় যদি A, C ও B একই সরলরেখার ভিন্ন ভিন্ন বিন্দু হয় এবং AC + CB = AB হয়। A, C ও B বিন্দু তিনটিকে সমরেখ বিন্দুও বলা হয়। A ও B এবং এদের অন্তবর্তী সকল বিন্দুর সেটকে A ও B বিন্দুর সংযোজক রেখাংশ বা সংক্ষেপে AB রেখাংশ বলা হয় ।

A ও B বিন্দুর অন্তর্বর্তী প্রত্যেক বিন্দুকে রেখাংশের অন্তঃস্থ বিন্দু বলা হয়। আবার, C বিন্দু এবং C বিন্দু থেকে AB সরলরেখা বরাবর কোন একদিকে অসীম পর্যন্ত বিন্দুর সেটকে রশ্মি বলা হয়। C বিন্দু AB সরলরেখাকে CA ও CB রশ্মিতে বিভক্ত করে।

 

 

কোণ (Angle)

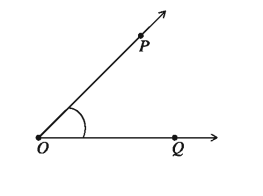
একই সমতলে দুইটি রশ্মির প্রান্তবিন্দু একই হলে কোণ তৈরি হয়। রশ্মি দুইটিকে কোণের বাহু এবং এদের সাধারণ বিন্দুকে শীর্ষবিন্দু বলে। চিত্রে, OP ও Q রশ্মিদ্বয় এদের সাধারণ প্রান্তবিন্দু O তে ∠POQ উৎপন্ন করেছে। O বিন্দুটি ∠POQ এর শীর্ষবিন্দু। OP এর যে পার্শ্বে Q আছে সেই পার্শ্বে এবং OQ এর যে পার্শ্বে P আছে সেই পার্শ্বে অবস্থিত সকল বিন্দুর সেটকে∠POQ এর অভ্যন্তর বলা হয়। কোণটির অভ্যন্তরে অথবা কোনো বাহুতে অবস্থিত নয় এমন সকল বিন্দুর সেটকে এর বহির্ভাগ বলা হয়।

 

 

সরল কোণ (Straight angle )

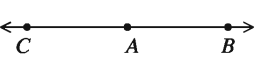
দুইটি পরস্পর বিপরীত রশ্মি এদের সাধারণ প্রান্তবিন্দুতে যে কোণ উৎপন্ন করে, তাকে সরল কোণ বলে। পাশের চিত্রে, AB রশ্মির প্রান্তবিন্দু A থেকে AB এর বিপরীত দিকে AC রশ্মি আঁকা হয়েছে। AC ও AB রশ্মিদ্বয় এদের সাধারণ প্রান্তবিন্দু A তে ∠BAC উৎপন্ন করেছে। ∠BAC কে সরল কোণ বলে। সরল কোণের পরিমাপ দুই সমকোণ বা 180°।

 

 

সন্নিহিত কোণ (Adjacent angle )

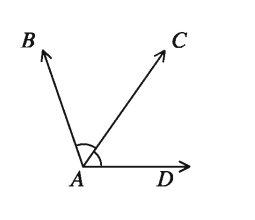
যদি সমতলে দুইটি কোণের একই শীর্ষবিন্দু হয় ও এদের একটি সাধারণ রশ্মি থাকে এবং কোণদ্বয় সাধারণ রশ্মির বিপরীত পাশে অবস্থান করে, তবে ঐ কোণদ্বয়কে সন্নিহিত কোণ বলে। পাশের চিত্রে, A বিন্দুটি ∠BAC ও ∠CAD এর শীর্ষবিন্দু। A বিন্দুতে ∠BAC ও ∠CAD উৎপন্নকারী রশ্মিগুলোর মধ্যে AC সাধারণ রশ্মি। কোণ দুইটি সাধারণ রশ্মি AC এর বিপরীত পাশে অবস্থিত। ∠BAC এবং ∠CAD পরস্পর সন্নিহিত কোণ।

 

 

লম্ব, সমকোণ (Right angle )

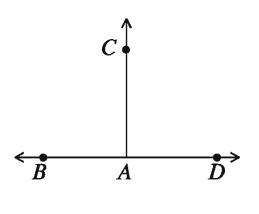
যদি একই রেখার উপর অবস্থিত দুইটি সন্নিহিত কোণ পরস্পর সমান হয়, তবে কোণ দুইটির প্রত্যেকটি সমকোণ বা 90°। সমকোণের বাহু দুইটি পরস্পরের উপর লম্ব। পাশের চিত্রে, BD রেখার A বিন্দুতে AC রশ্মি দ্বারা ∠BAC ও ∠DAC দুইটি কোণ উৎপন্ন হয়েছে। A বিন্দু কোণ দুইটির শীর্ষবিন্দু।

∠BAC ও ∠DAC উৎপন্নকারী বাহুগুলোর মধ্যে AC সাধারণ বাহু। কোণ দুইটি সাধারণ বাহু AC এর দুই পাশে অবস্থিত। ∠BAC এবং ∠DAC পরস্পর সমান হলে, এদের প্রত্যেকটিকে সমকোণ বলে। AC ও BD বাহুদ্বয় পরস্পরের উপর লম্ব।

 

 

সূক্ষ্মকোণ ও স্থূলকোণ (Acute angle and obtuse angle )

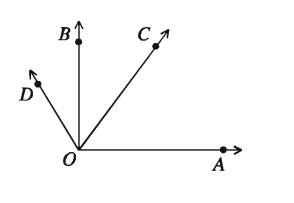
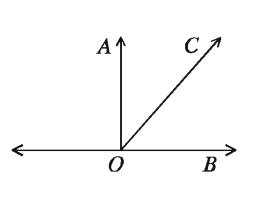
এক সমকোণ থেকে ছোট কোণকে সূক্ষ্মকোণ এবং এক সমকোণ থেকে বড় কিন্তু দুই সমকোণ থেকে ছোট কোণকে স্থূলকোণ বলা হয়। চিত্রে ∠AOC সূক্ষ্মকোণ এবং ∠AOD স্থূলকোণ। এখানে ∠AOB এক সমকোণ ।

 

 

প্রবৃদ্ধ কোণ (Reflex angle )

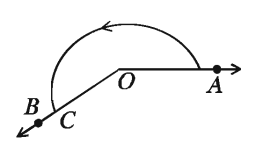
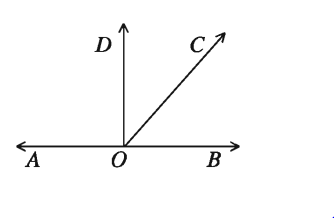
দুই সমকোণ থেকে বড় কিন্তু চার সমকোণ থেকে ছোট কোণকে প্রবৃদ্ধ কোণ বলা হয়। চিত্রে চিহ্নিত ∠AOC প্রবৃদ্ধ কোণ।

 

 

পূরক কোণ (Complementary angle )

দুইটি কোণের পরিমাপের যোগফল এক সমকোণ হলে কোণ দুইটির একটি অপরটির পূরক কোণ।

পাশের চিত্রে, ∠AOB একটি সমকোণ। OC রশ্মি কোণটির বাহুদ্বয়ের অভ্যন্তরে অবস্থিত। এর ফলে ∠AOC এবং ∠COB এই দুইটি কোণ উৎপন্ন হলো। কোণ দুইটির পরিমাপের যোগফল ∠AOB এর পরিমাপের সমান, অর্থাৎ এক সমকোণ। ∠AOC এবং ∠COB পরস্পর পূরক কোণ।

 

 

সম্পূরক কোণ (Supplementary angle )

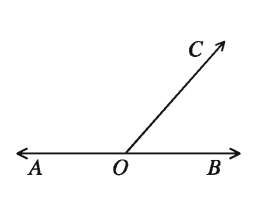
দুইটি কোণের পরিমাপের যোগফল দুই সমকোণ হলে কোণ দুইটি পরস্পর সম্পূরক কোণ পাশের চিত্রে, O, AB সরলরেখার অন্তঃস্থ একটি বিন্দু। OC একটি রশ্মি যা OA রশ্মি ও OB রশ্মি থেকে ভিন্ন। এর ফলে ∠AOC এবং ∠COB এই দুইটি কোণ উৎপন্ন হলো। কোণ দুইটির পরিমাপের যোগফল ∠AOB কোণের পরিমাপের সমান, অর্থাৎ দুই সমকোণ, কেননা ∠AOB একটি সরলকোণ। ∠AOC এবং ∠COB পরস্পর সম্পূরক কোণ।

 

 

বিপ্রতীপ কোণ (Vertical angle )

কোনো কোণের বাহুদ্বয়ের বিপরীত রশ্মিদ্বয় যে কোণ তৈরি করে তা ঐ কোণের বিপ্রতীপ কোণ ।

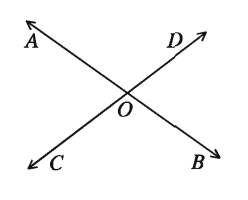
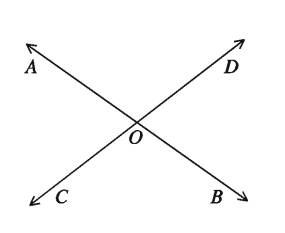
চিত্রে OA ও OB পরস্পর বিপরীত রশ্মি। আবার OC ও OD পরস্পর বিপরীত রশ্মি। ∠BOD ও ∠AOC পরস্পর বিপ্রতীপ
কোণ।

আবার ∠BOC ও ∠DOA একটি অপরটির বিপ্রতীপ কোণ। দুইটি সরলরেখা কোনো বিন্দুতে পরস্পরকে ছেদ করলে, ছেদ বিন্দুতে দুই জোড়া বিপ্রতীপ কোণ উৎপন্ন হয়।

 

 

উপপাদ্য ১.

একটি সরলরেখার একটি বিন্দুতে অপর একটি রশ্মি মিলিত হলে, যে দুইটি সন্নিহিত কোণ উৎপন্ন হয় এদের সমষ্টি দুই সমকোণ

প্রমাণ:

মনে করি, AB সরলরেখাটির O বিন্দুতে OC রশ্মির প্রান্তবিন্দু মিলিত হয়েছে। ফলে ∠AOC ও ∠COB দুইটি সন্নিহিত কোণ উৎপন্ন হল। AB রেখার উপর DO লম্ব আঁকি। সন্নিহিত কোণদ্বয়ের সমষ্টি

= ∠AOC+ ∠COB = ∠AOD + ∠DOC + ∠COB

= ∠AOD + ∠DOB = 2 সমকোণ।

 

 

 

উপপাদ্য ২.

দুইটি সরলরেখা পরস্পর ছেদ করলে, উৎপন্ন বিপ্রতীপ কোণগুলো পরস্পর সমান ।

মনে করি, AB ও CD রেখাদ্বয় পরস্পর O বিন্দুতে ছেদ করেছে। ফলে O বিন্দুতে ∠AOC, ∠COB, ∠BOD, ∠AOD কোণ উৎপন্ন হয়েছে।

∠AOC = বিপ্রতীপ ∠BOD এবং ∠COB = বিপ্রতীপ ∠AOD