আজকে আমরা সূচকীয়, লগারিদমীয় ও পরমমান ফাংশন সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের সূচকীয় ও লগারিদমীয় ফাংশন অংশের অন্তর্গত।

সূচকীয়, লগারিদমীয় ও পরমমান ফাংশন
প্রথম অধ্যায়ে আমরা ফাংশন সম্পর্কে বিস্তারিত জেনেছি। এখানে সূচকীয়, লগারিদমীয় ও পরমমান ফাংশন সম্পর্কে আলোচনা কর হল:
সূচকীয় ফাংশন
নিচের তিনটি সারণীতে বর্ণিত (x, y) ক্রমজোড়ের মানগুলো লক্ষ করি:
সারণি ১ এ বর্ণিত x এর ভিন্ন ভিন্ন মানের জন্য y এর মানগুলোর অন্তর সমান যা দ্বারা ফাংশনটি বর্ণিত হয়েছে। ইহা একটি সরলরেখার সমীকরণ।
|
x |
-2 | -1 | 0 | 1 | 2 | 3 |
|
y |
-4 | -2 | 0 | 2 | 4 | 6 |
সারণি ২ এ বর্ণিত (x, y) ক্রমজোড়ের মানগুলো দ্বারা দ্বিঘাত সমীকরণ y = x2 ফাংশনটি বর্ণিত হয়েছে।
|
x |
0 | 1 | 2 | 3 | 4 | 5 |
|
y |
0 | 1 | 4 | 9 | 16 | 25 |
সারণি ৩ এ বর্ণিত (x, y) ক্রমজোড়ের মানগুলো = 2 দ্বারা বর্ণনা করা যায়। এখানে 2 একটি নির্দিষ্ট বাস্তব সংখ্যা এবং x এর ভিন্ন ভিন্ন মানের জন্য y এর বর্ণিত মানগুলো পাওয়া যায়।
|
x |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
y |
1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
সূচক ফাংশন f(x) = a* সকল বাস্তব সংখ্যা x এর জন্য সংজ্ঞায়িত, যেখানে a > 0 এবং a = 1 যেমন y = 2*, 10*, **e* ইত্যাদি সূচক ফাংশন।
দ্রষ্টব্য:
সূচক ফাংশন f(x) = ax এর ডোমেন (– ∞, ∞) এবং রেঞ্জ = (0, ∞ )
f(x) = 2x এর লেখচিত্র অঙ্কন
|
x |
-3 | -2 | -1 | 0 | 1 | 2 |
|
y |
1/8 | 1/4 | 1/2 | 1 | 2 | 4 |
y = 2x ধরে x এর কয়েকটি মানের জন্য y এর সংশ্লিষ্ট মানগুলোর তালিকা প্রস্তুত করি।
ছক কাগজে (x, y) এর মানগুলো স্থাপন করলে পাশের লেখচিত্র পাওয়া যায়।
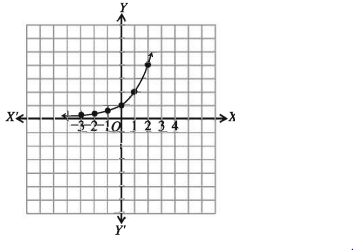
চিত্র লক্ষ করি:
(i) x ঋণাত্মক এবং |x| যথেষ্ট বড় হলে y এর মান ০ (শূন্য) এর কাছাকাছি হয় যদিও কখনো শূন্য হয় না অর্থাৎ, x → -∞ হলে y → 0 হয়
(ii) x ধনাত্মক এবং x যথেষ্ট বড় হলে y এর মান যথেষ্ট বড় হয়। অর্থাৎ x 0 হলে y এ থেকে বুঝা যায় f(x) = 2° ফাংশনের রেঞ্জ (0, ০০) ।
লগারিদমীয় ফাংশন
যেহেতু সূচক ফাংশন একটি এক-এক ফাংশন। সুতরাং এর বিপরীত ফাংশন আছে।
f(x) = y = ax এর বিপরীত ফাংশন f−1(y) = x = logay
অর্থাৎ x হলো y এর a ভিত্তিক লগারিদম।
সংজ্ঞা:
লগারিদমিক ফাংশন f(x) = logar দ্বারা সংজ্ঞায়িত যেখানে a > 0 এবং a ≠ 1।
যেমন, f(x) = log3x, logex, log1ox ইত্যাদি লগারিদমীয় ফাংশন।
y = log2x এর লেখচিত্র অঙ্কন
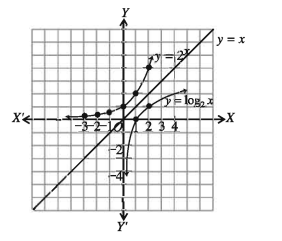
যেহেতু y = log2x ফলে y = 2″ এর বিপরীত ফাংশন। y = x রেখার সাপেক্ষে সূচক ফাংশনের প্রতিফলন লগারিদমীয় ফাংশন নির্ণয় করা হয়েছে যাহা y = x রেখার সাপেক্ষে প্রতিসম।
এখানে ডোমেন R. (0, ∞) এবং রেঞ্জ D = (-∞, ∞)
উদাহরণ ৩০.
f(x): = x\|x| , ফাংশনটির ডোমেন এবং রেঞ্জ নির্ণয় কর।
সমাধান:
f (0) =0/ |0| যা অসংজ্ঞায়িত।
x = 0 বিন্দুতে প্রদত্ত ফাংশনটি বিদ্যমান নয়। শূন্য ব্যতিত x এর অন্য বাস্তব মানের জন্য প্রদত্ত ফাংশনটি বিদ্যমান।
ফাংশনের ডোমেন Df = R – {0}
\f(x): = x\|x| = x\ x = 1যখন x > 0, x\ x = – 1 যখন x < 0
ফাংশনের রেঞ্জ Rj = {-1, 1}
উদাহরণ ৩১.
y = f(x) = ln(a+x)/(a-x) a > 0 এবং পূর্ণসংখ্যা, ফাংশনটির ডোমেন ও রেঞ্জ নির্ণয় কর।
সমাধান:
যেহেতু লগারিদম শুধুমাত্র ধনাত্মক বাস্তব সংখ্যার জন্য সংজ্ঞায়িত হয়
(a+x)/(a-x)> ০ যদি
(i) a + x > 0 এবং a – x > 0 হয় অথবা
(ii) a + x < 0 এবং a − x < 0 হয়
(i) ⇒ x = – a এবং a > x
⇒ – a < x এবং x <a
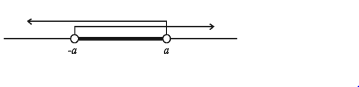
ডোমেন = {x:-a < x}∩ {x: x < a}
(-a,∞)∩(-∞, a) = (−a, a)
(ii) ⇒ x < -a এবং a < x
⇒ x < -a এবং > a
ডোমেন = {x: x < -a}∩ {x: x > a} = Ø.
প্রদত্ত ফাংশনের ডোমেন Df = (i) ও (ii) থেকে প্রাপ্ত ডোমেনের সংযোগ (a, a) U = (-a, a)
রেঞ্জ y= f(x) = In(a + x)/( a-x)
ey (a + x)/( a-x)
a+x=aey – xey
x + xey = aey – a
(1+ey) x = a(ey – 1)
⇒ x = a(ey – 1)/ ey + 1
y এর সকল বাস্তব মানের জন্য x এর মান বাস্তব হয়।
প্রদত্ত ফাংশনের রেঞ্জ RJ = R
পরমমান
নবম-দশম শ্রেণির গণিতে এ সম্পর্কে বিস্তারিত বর্ণনা করা হয়েছে। এখানে শুধুমাত্র পরমমানের সংজ্ঞা দেওয়া হলো।
যেকোনো বাস্তব সংখ্যা x এর মান শূন্য, ধনাত্মক বা ঋণাত্মক। কিন্তু x এর পরমমান সবসময়ই শূন্য – বা ধনাত্মক। এর পরমমানকে |x | দ্বারা প্রকাশ করা হয় এবং পরমমান নিম্নলিখিতভাবে সংজ্ঞায়িত করা হয়।
|x | = x, যখন x ≤ 0 — x, যখন x < 0 =
উদাহরণ ৩২
|0 | = 0, |3| = 3, | − 3| = − (-3) = 3
পরমমমান ফাংশন (Absolute Value Function)
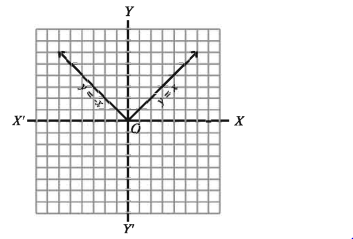
যদি x ∈ R হয় তবে y = f(x) = \x\ = x যখন x ≤ 0 – x যখন x < 0 কে পরমমমান ফাংশন বলা হয়।
ডোমেন D = R এবং রেঞ্জ Rj = [0,00)
উদাহরণ ৩৩
f(x) = e^(-\x\/2) যখন − 1 < x < 0। এর ডোমেন ও রেঞ্জ নির্ণয় কর।
সমাধান:
f(x) = e^(-\x\/2), − 1 < < 0
এর মান যেহেতু – 1 থেকে 0 এর মধ্যে নির্দিষ্ট।
সুতরাং ডোমেন Df = (–1,0)
আবার −1 < x < 0 ব্যবধিতে f(x) ∈ (e^-1/2, 1)
সুতরাং রেঞ্জ f = (e 2, 1 )
