আজকে আমাদের আলোচনার বিষয়ঃ লৈখিক পদ্ধতি। এটি নবম – দশম শ্রেনী গণিতের দুই চলকবিশিষ্ট সরল সহসমীকরণ এর অন্তর্গত।

লৈখিক পদ্ধতি (Graphical Method)
দুই চলকবিশিষ্ট একটি সরল সমীকরণে বিদ্যমান চলক x ও y এর সম্পর্ককে চিত্রের সাহায্যে প্রকাশ করা যায়। এই চিত্রকে ঐ সম্পর্কের লেখচিত্র বলে। এ জাতীয় সমীকরণের লেখচিত্রে অসংখ্য বিন্দু থাকে। এরূপ কয়েকটি বিন্দু স্থাপন করে এদের পরস্পর সংযুক্ত করলেই লেখচিত্র পাওয়া যায়।
সরল সহসমীকরণের প্রত্যেকটির অসংখ্য সমাধান রয়েছে। প্রত্যেকটি সমীকরণের লেখ একটি সরলরেখা। সরলরেখাটির প্রত্যেকটি বিন্দুর স্থানাঙ্ক সমীকরণটিকে সিদ্ধ করে। কোনো লেখ নির্দিষ্ট করতে তিন বা ততোধিক বিন্দু আবশ্যক। এখন আমরা নিচের সমীকরণজোটটি সমাধান করার চেষ্টা করবো:
2x + y = 3… ( 1 )
4x + 2y = 6… (2)
সমীকরণ (1) থেকে পাই, y = 3 – 2x
সমীকরণটিতে x এর কয়েকটি মান নিয়ে এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
-1 |
0 |
3 |
|
y |
5 |
3 |
-3 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (–1, 5), (0, 3 ) ও ( 3, 3 ) ।
আবার, সমীকরণ (2) থেকে পাই, 2y = 6 – 4x বা, y= ( 6 – 4x )/2
সমীকরণটিতে x এর কয়েকটি মান নিয়ে y এর অনুরূপে মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
-2 |
0 |
3 |
|
y |
7 |
3 |
-9 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (−2, 7), (0, 3 ) ও (6, – 9 ) ।
মনে করি, ছক কাগজে XOX ও YOY’ যথাক্রমে x অক্ষ ও y-অক্ষ এবং O মূলবিন্দু।
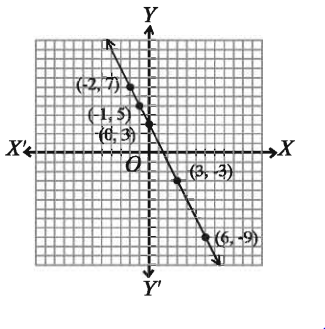
ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি। এখন সমীকরণ (1) হতে প্রাপ্ত ( – 1,5 ), ( 03 ) ( 3 − 3 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। লেখটি একটি সরলরেখা।
আবার, সমীকরণ (2) হতে প্রাপ্ত (−2, 7), (0, 3) ও ( 6, 9 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। এক্ষেত্রেও লেখটি একটি সরলরেখা।
তবে লক্ষ করি, সরলরেখা দুইটি পরস্পরের উপর সমাপতিত হয়ে একটি সরলরেখায় পরিণত হয়েছে। আবার, সমীকরণ (2) এর উভয়পক্ষকে 2 দ্বারা ভাগ করলে সমীকরণ (1) পাওয়া যায়। এ কারণে সমীকরণদ্বয়ের লেখ পরস্পর সমাপতিত হয়েছে।
এখানে, 2x + y = 3… (1)
4x+2y= 6… (2)
সমীকরণজোটটি সমঞ্জস ও পরস্পর নির্ভরশীল। এরূপ সমীকরণজোটের অসংখ্যা সমাধান আছে এবং সমীকরণজোটটির লেখ একটি সরলরেখা।
এবার আমরা নিচের সমীকরণজোটটি সমাধান করার চেষ্টা করব:
2x – y = 4… ( 1 )
4x – 2y = 12 … (2)
সমীকরণ (1) থেকে পাই, y = 2x – 4
সমীকরণটিতে x এর কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি :
|
x |
-1 |
0 |
4 |
|
y |
-6 |
-4 |
4 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (–1, 6 ), (0, – 4 ), ( 4, 4 ) ।
আবার, সমীকরণ (2) থেকে পাই,
4x – 2y = 12, বা, 2x – y = 6 [ উভয়পক্ষকে 2 দ্বারা ভাগ করে ]
বা, y = 2x – 6
সমীকরণটিতে x এর কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
0 |
3 |
6 |
|
y |
-6 |
0 |
6 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (0, 6 ), ( 3,0 ), ( 6,6 )
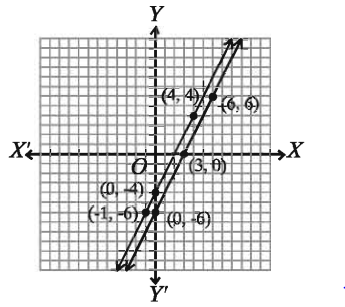
মনে করি, ছক কাগজে XOX ও YOY’ যথাক্রমে x অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর
ক্ষুদ্রতম বর্গক্ষেত্রের প্রতিবাহুর দৈর্ঘ্যকে একক ধরে সমীকরণ (1) হতে প্রাপ্ত (–1, – 6), (0, – 4 ) ও ( 4, 4 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। লেখটি একটি সরলরেখা।
আবার, সমীকরণ (2) হতে প্রাপ্ত ( 0 – 6 ), ( 3,0), ( 66 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। এক্ষেত্রেও লেখটি একটি সরলরেখা।
চিত্রে লক্ষ করি, প্রদত্ত সমীকরণদ্বয়ের পৃথকভাবে প্রত্যেকটির অসংখ্য সমাধান থাকলেও জোট হিসেবে এদের সাধারণ সমাধান নেই। আরও লক্ষ করি যে, প্রদত্ত সমীকরণ দুইটির লেখচিত্র দুইটি পরস্পর সমান্তরাল সরলরেখা। অর্থাৎ, রেখা দুইটি কখনো একে অপরকে ছেদ করবে না। অতএব, এদের কোনো সাধারণ ছেদ বিন্দু পাওয়া যাবে না। এ ক্ষেত্রে আমরা বলি যে, এরূপ সমীকরণজোটের কোনো সমাধান নেই। আমরা জানি, এরূপ সমীকরণজোট অসমঞ্জস ও পরস্পর অনির্ভরশীল।
আমরা এখন লেখচিত্রের সাহায্যে সমঞ্জস ও পরস্পর অনির্ভরশীল সমীকরণজোট সমাধান করবো।
দুই চলকবিশিষ্ট দুইটি সমঞ্জস ও পরস্পর অনির্ভরশীল সরল সমীকরণের লেখ একটি বিন্দুতে ছেদ করে। ঐ ছেদ বিন্দুর স্থানাঙ্ক দ্বারা উভয় সমীকরণ সিদ্ধ হবে। ছেদবিন্দুটির স্থানাঙ্কই হবে সমীকরণদ্বয়ের সমাধান।
উদাহরণ ৮.
সমাধান কর ও সমাধান লেখচিত্রে দেখাও :
2x + y = 8
3x-2y= 5
সমাধান:
প্রদত্ত সমীকরণদ্বয়
2x + y – 8 = 0… (1)
3x-2y-50… (2)
আড়গুণন পদ্ধতিতে পাই,
x/1 × (-5) – ( 2 ) x (8) = y/ (-8) x 3 -(-5) x 2 = 1/ 2 (-2) – 3 x 1
বা, x/-5 -16 = y/ -24 + 10 = 1/-4 -3
বা, x/-21 = y/ -14 = 1/-7
বা, x/21 = y/14 = 1/7
x/21 = 1/7
বা, x = 21/7 = 3
আবার, y/14 = 1/7, y = 14/7 = 2
সমাধান: (x, y) = (3, 2)
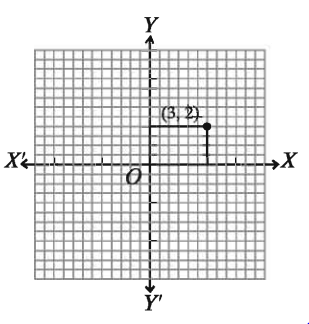
মনে করি, XOX ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গের প্রতি দুই বাহুর দৈর্ঘ্যকে একক ধরে (3, 2) বিন্দুটি স্থাপন করি।
উদাহরণ ৯.
লেখচিত্রের সাহায্যে সমাধান কর:
3x – y = 3
5x + y = 21
সমাধান: প্রদত্ত সমীকরণদ্বয়
3x – y = 3… ( 1 )
5x + y = 21… (2)
সমীকরণ (1) থেকে পাই, 3x – y = 3, বা, y = 3x – 3
সমীকরণটিতে x এর কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
-1 |
0 |
3 |
|
y |
-6 |
-3 |
6 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (–1, 6 ), ( 0 ,– 3), ( 3, 6 )
আবার, সমীকরণ (2) থেকে পাই, 5x + y = 21, বা, y = 21 – 5x
সমীকরণটিতে x এর কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
3 |
4 |
5 |
|
y |
6 |
1 |
-4 |
সমীকরণটির লেখের উপর তিনটি বিন্দু ( 3, 6 ), ( 4, 1 ), ( 5, – 4 ) ।
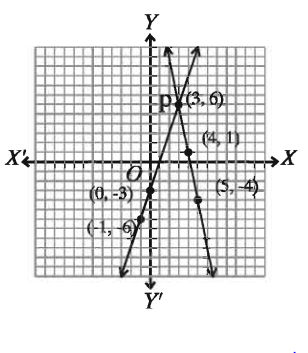
মনে করি, XOX ও YOY’ যথাক্রমে -অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি। এখন ছক কাগজে সমীকরণ (1) হতে প্রাপ্ত (–1, 6), (0, 3), ( 3, 6 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। লেখটি একটি সরলরেখা।
একইভাবে, সমীকরণ (2) হতে প্রাপ্ত ( 3, 6), ( 4, 1 ), ( 5, 4 ) বিন্দুগুলো স্থাপন করি ও এদের পরস্পর সংযুক্ত করি। এক্ষেত্রেও লেখটি একটি সরলরেখা। মনে করি, সরলরেখাদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে। চিত্র
থেকে দেখা যায়, P বিন্দুর স্থানাঙ্ক ( 3, 6 )
সমাধান:
(x, y) = ( 3, 6 )
উদাহরণ ১০.
লৈখিক পদ্ধতিতে সমাধান কর :
2x + 5y = -14
4x-5y = 17
সমাধান:
প্রদত্ত সমীকরণদ্বয়
2x + 5y = -14… ( 1 )
4x – 5y = 17… (2)
সমীকরণ (1) থেকে পাই, 5y = 14 – 2x, বা, y = – 2x – 14/ 5
সমীকরণটিতে x এর সুবিধামত কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
3 |
1/2 |
-2 |
|
y |
-4 |
-3 |
-2 |
সমীকরণটির লেখের উপর তিনটি বিন্দু ( 3 – 4), (1/2,-3), (-2,-2)
আবার, সমীকরণ (2) থেকে পাই, 5y = 4x – 17, বা, y = (4x -17)/ 5
সমীকরণটিতে x এর সুবিধামত কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
3 |
1/2 |
-2 |
|
y |
-1 |
-3 |
-5 |
সমীকরণটির লেখের উপর তিনটি বিন্দু (3, -1), (1/2, -3), (-2,-5)
মনে করি, XOX’ ও YOY’ যথাক্রমে -অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গের প্রতি দুই বাহুর দৈর্ঘ্যকে একক ধরি। এখন, ছক কাগজে সমীকরণ (1) থেকে প্রাপ্ত ( 3, 4), (-2,-2) বিন্দুগুলো স্থাপন করে এদের পরপর সংযুক্ত করি। লেখটি একটি সরলরেখা।
একইভাবে, সমীকরণ (2) থেকে প্রাপ্ত 5 (3,-1), (1/2,-3), (−2, –5) বিন্দুগুলো স্থাপন করে এদের পরপর সংযুক্ত করি। লেখটি একটি সরলরেখা।
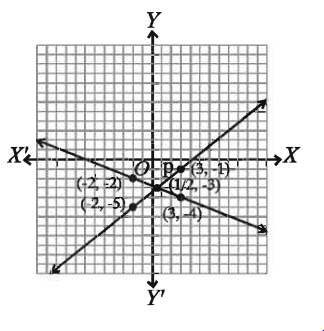
মনে করি, সরলরেখাদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে। চিত্রে দেখা যায়, P বিন্দুর স্থানাঙ্ক (1/2-3)
সমাধান: (x, y) = 1/2-3)
উদাহরণ ১১.
লেখের সাহায্যে সমাধান কর: 3 – 3/2x = 8 – 4x
সমাধান:
প্রদত্ত সমীকরণ 3 – 3/2x = 8 – 4x
ধরি, y = 3 – 3/2x =1 = 8 – 4x
y = 3 – 3/2x… (1)
এবং y = 8 – 4x … (2)
এখন, সমীকরণ (1) এ x এর কয়েকটি মান নিয়ে y এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
-2 |
0 |
2 |
|
y |
6 |
3 |
0 |
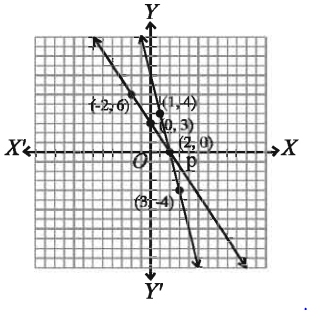
সমীকরণটির লেখের উপর তিনটি বিন্দু (-2, 6), (0, 3), ( 2,0)
আবার, সমীকরণ (2) এ x-এর কয়েকটি মান নিয়ে y-এর অনুরূপ মান বের করি ও নিম্নের ছকটি তৈরি করি:
|
x |
1 |
2 |
3 |
|
y |
4 |
0 |
-4 |
সমীকরণটির লেখের উপর তিনটি বিন্দু ( 1, 4), (2, 0 ), ( 3, 4 )
মনে করি, XOX ও YOY’ যথাক্রমে x-অক্ষ ও y-অক্ষ এবং O মূলবিন্দু। ছক কাগজের উভয় অক্ষ বরাবর ক্ষুদ্রতম বর্গের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি। এখন, ছক কাগজে সমীকরণ (1) থেকে প্রাপ্ত (-2, 6), (0, 3), (2, 0 ) বিন্দুগুলো স্থাপন করি ও বিন্দুগুলো পরপর সংযুক্ত করি। তাহলে, লেখটি X2- হবে একটি সরলরেখা।
একইভাবে, সমীকরণ (2) থেকে প্রাপ্ত (1, 4), (2, 0 ), ( 3, 4) বিন্দুগুলো স্থাপন করে এগুলো পরপর সংযুক্ত করি। তাহলে, লেখটি হবে একটি সরলরেখা।
মনে করি, সরলরেখাদ্বয় পরস্পর P বিন্দুতে ছেদ করে। চিত্রে দেখা যায়, P ছেদবিন্দুটির স্থানাঙ্ক (2,0)
সমাধান: x = 2
অনুশীলনী
লেখচিত্রের সাহায্যে সমাধান কর:
১. 3x + 4y = 14
4x – 3y = 2
২. 2x – y = 1
5x + y = 13
৩. 2x + 5y = 1
x + 3y = 2
8. 3x – 2y = 2
5x – 3y = 5
৫. x/2 + y/3 = 2
2x + 3y = 13
৬. 3x + y = 6
5x + 3y = 12
৭. 3x + 2y = 4
3x – 4y = 1
৮. x/2+ y/3 = 3
x + y/6 = 3
৯. 3x + 2 = x – 2
১০. 3x – 7 = 3 – 2x
