আজকে আমাদের আলোচনার বিষয়ঃ স্বাভাবিক সংখ্যার প্যাটার্ন । এটি অষ্টম শ্রেনী গণিতের প্যাটার্ন অংশের অন্তর্গত।
স্বাভাবিক সংখ্যার প্যাটার্ন
প্যাটার্ন
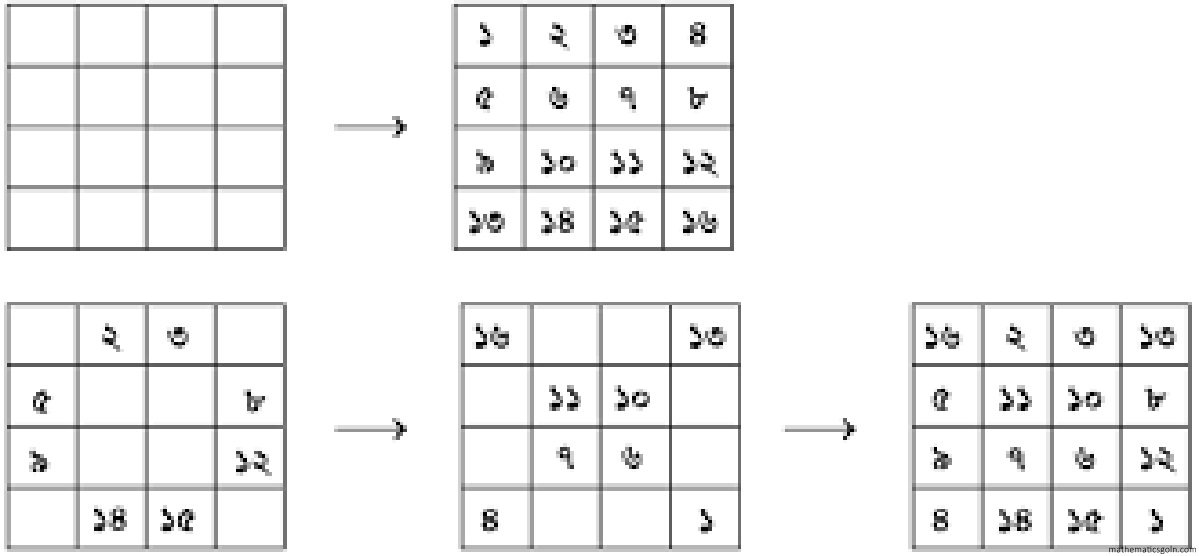
নিচের প্রথম চিত্রের টাইলসগুলো লক্ষ করি। এগুলো একটি প্যাটার্নে সাজানো হয়েছে। এখানে প্রতিটি আড়াআড়ি টাইলস্ এর পাশের টাইলটি লম্বালম্বিভাবে সাজানো। সাজানোর এই নিয়মটি একটি প্যাটার্ন সৃষ্টি করেছে।

দ্বিতীয় চিত্রে কতগুলো সংখ্যা ত্রিভুজাকারে সাজানো হয়েছে। সংখ্যাগুলো একটি বিশেষ নিয়ম মেনে নির্বাচন করা হয়েছে । নিয়মটি হলো: প্রতি লাইনের শুরুতে ও শেষে ১ থাকবে এবং অন্য সংখ্যাগুলো উপরের সারির দুইটি পাশাপাশি সংখ্যার যোগফলের সমান। যোগফল সাজানোর এই নিয়ম অন্য একটি প্যাটার্ন সৃষ্টি করেছে।
আবার, ১, ৪, ৭, ১০, ১৩, … সংখ্যাগুলোতে একটি প্যাটার্ন বিদ্যমান। সংখ্যাগুলো ভালোভাবে লক্ষ করে দেখলে একটি নিয়ম খুঁজে পাওয়া যাবে। নিয়মটি হলো, ১ থেকে শুরু করে প্রতিবার ৩ যোগ করতে হবে । অন্য একটি উদাহরণ : ২, ৪, ৮, ১৬, ৩২, … প্রতিবার দ্বিগুণ হচ্ছে ।
মৌলিক সংখ্যা নির্ণয়
আমরা জানি যে, ১-এর চেয়ে বড় যে সব সংখ্যার ১ ও সংখ্যাটি ছাড়া অন্য কোনো গুণনীয়ক নেই, সেগুলো মৌলিক সংখ্যা । ইরাটোস্থিনিস (Eratosthenes) ছাঁকনির সাহায্যে সহজেই মৌলিক সংখ্যা নির্ণয় করা যায় । ১ থেকে ১০০ পর্যন্ত স্বাভাবিক সংখ্যাগুলো একটি চার্টে লিখি । এবার সবচেয়ে ছোট মৌলিক সংখ্যা ২ চিহ্নিত করি এবং এর গুণিতকগুলো কেটে দেই। এরপর ক্রমান্বয়ে ৩, ৫ এবং ৭ ইত্যাদি মৌলিক সংখ্যার গুণিতকগুলো কেটে দিই । তালিকায় যে সংখ্যাগুলো টিকে রইল সেগুলো মৌলিক সংখ্যা ।

সংখ্যা শ্রেণির নির্দিষ্ট সংখ্যা নির্ণয়
উদাহরণ ১।
সংখ্যাগুলোর পরবর্তী দুইটি সংখ্যা নির্ণয় কর : ৩, ১০, ১৭, ২৪, ৩১, …
সমাধান :

লক্ষ করি, প্রতিবার পার্থক্য ৭। অতএব, পরবর্তী দুইটি সংখ্যা হবে যথাক্রমে ৩১+৭ = ৩৮ ও ৩৮+৭ =৪৫।
উদাহরণ ২।
সংখ্যাগুলোর পরবর্তী সংখ্যাটি নির্ণয় কর: ১, ৪, ৯, ১৬, ২৫, …
সমাধান :

লক্ষ করি, প্রতিবার পার্থক্য ২ করে বাড়ছে । অতএব, পরবর্তী সংখ্যা হবে ২৫ + (৯ + ২) = ২৫ + ১১ = ৩৬।
উদাহরণ ৩।
সংখ্যাগুলোর পরবর্তী সংখ্যাটি নির্ণয় কর: ১, ৫, ৬, ১১, ১৭, ২৮, ….
সমাধান :

প্রদত্ত সংখ্যাগুলো একটি প্যাটার্নে লেখা হয়েছে । পরপর দুইটি সংখ্যার যোগফল পরবর্তী সংখ্যাটির
সমান । অতএব, পরবর্তী সংখ্যাটি হবে ১৭ + ২৮ = ৪৫।
স্বাভাবিক ক্রমিক সংখ্যার যোগফল নির্ণয়
স্বাভাবিক ক্রমিক সংখ্যার যোগফল বের করার একটি চমৎকার সূত্র রয়েছে । আমরা সহজেই সূত্রটি বের করতে পারি ।
মনে করি, ১ থেকে ১০ পর্যন্ত ক্রমিক স্বাভাবিক সংখ্যাগুলোর যোগফল ক ৷
অর্থাৎ,ক = ১ + ২ + ৩ + ৪ + ৫ + ৬ + ৭ + ৮ + ৯ + ১০
লক্ষ করি, প্রথম ও শেষ পদের যোগফল ১ + ১০ = ১১, দ্বিতীয় ও শেষ পদের আগের পদের যোগফলও ২ + ৯ = ১১ ইত্যাদি । একই যোগফলের প্যাটার্ন অনুসরণ করে ৫ জোড়া সংখ্যা পাওয়া গেল । সুতরাং যোগফল ১১ × ৫ = ৫৫। এ থেকে স্বাভাবিক ক্রমিক সংখ্যার যোগফল বের করার একটি কৌশল পাওয়া গেল ।
কৌশলটি হলো :
প্রদত্ত যোগফলের সাথে সংখ্যাগুলো বিপরীত ক্রমে লিখে যোগ করে পাই
ক =১ + ২ + ৩ + ৪ + ৫ + ৬ + ৭ + ৮ + ৯ + ১০
ক = ১০ + ৯ + ৮ + ৭ + ৬ + 5 + ৪ + ৩ + ২ + ১
২ক = (১+১০) + (২+৯) + … + (৯+২) + (১০+১)
বা, ২ক = (১+১০)× ১০
বা, ক = {(১+১০)× ১০}/২ = (১১ × ১০)/২ = ৫৫
যোগফল = {(প্রথম সংখ্যা + শেষ সংখ্যা ) x পদ সংখ্যা}/২
প্রথম দশটি বিজোড় সংখ্যার যোগফল নির্ণয়
প্রথম দশটি বিজোড় সংখ্যার যোগফল কত? ক্যালকুলেটরের সাহায্যে সহজেই যোগফল পাই, ১০০।
১ + ৩ + ৫ + ৭ + ৯ + ১১ + ১৩ + ১৫ + ১৭ + ১৯ = ১০০
এভাবে প্রথম পঞ্চাশটি বিজোড় সংখ্যার যোগফল বের করা সহজ হবে না। বরং এ ধরনের যোগফল নির্ণয়ের জন্য কার্যকর গাণিতিক সূত্র তৈরি করি। ১ থেকে ১৯ পর্যন্ত বিজোড় সংখ্যাগুলো লক্ষ করলে দেখা যায়, ১ + ১৯ = ২০, ৩ + ১৭ = ২০, ৫ + ১৫ = ২০ ইত্যাদি । এরকম ৫ জোড়া সংখ্যা পাওয়া যায় যাদের প্রত্যেক জোড়ার যোগফল ২০ । সুতরাং, সংখ্যা গুলোর যোগফল ৫ × ২০ = ১00 |
আমরা লক্ষ করি,
১ + ৩ = ৪, একটি পূর্ণবর্গ সংখ্যা
১ + ৩ + ৫ = ৯, একটি পূর্ণবর্গ সংখ্যা
১ + ৩ + ৫ + ৭ = ১৬, একটি পূর্ণবর্গ সংখ্যা, ইত্যাদি ।
প্রতিবার যোগফল একটি পূর্ণবর্গ সংখ্যা পাচ্ছি । বিষয়টি জ্যামিতিক প্যাটার্ন হিসেবে সহজেই ব্যাখ্যা করা যায় । ক্ষুদ্রাকৃতির বর্গের সাহায্যে এই যোগফলের প্যাটার্ন লক্ষ করি ।
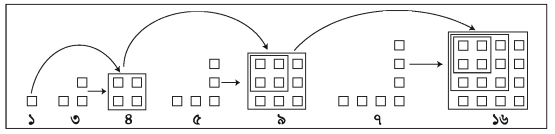
দেখা যাচ্ছে যে প্রথম দুইটি ক্রমিক বিজোড় সংখ্যার যোগের বেলায় প্রত্যেক পাশে ২টি করে ছোট বর্গ বসানো হয়েছে। আবার, প্রথম তিনটি ক্রমিক বিজোড় সংখ্যা যোগের বেলায় প্রত্যেক পাশে ৩টি ছোট বর্গ বসানো হয়েছে । সুতরাং, ১০টি ক্রমিক বিজোড় সংখ্যা যোগ করলে চিত্রের প্রত্যেক পাশে ১০টি ছোট বর্গ থাকবে । অর্থাৎ, ১০ x ১০ = ১০২ বা ১০০টি বর্গের প্রয়োজন হবে। সাধারণভাবে বলা যায় যে, ‘ক’ সংখ্যক ক্রমিক স্বাভাবিক বিজোড় সংখ্যার যোগফল ক’।
সংখ্যাকে দুইটি স্বাভাবিক সংখ্যার বর্গের সমষ্টি রূপে প্রকাশ
কিছু স্বাভাবিক সংখ্যা রয়েছে যেগুলোকে দুইটি স্বাভাবিক সংখ্যার বর্গের সমষ্টিরূপে প্রকাশ করা যায় ৷
যেমন, ২ = ১^২ + ১^২
৫ = ১^২+ ২^২
৮ = ২^২ + ২^২
১০ = ১^২ + ৩^২
১৩ = ২^২ + ৩^২ ইত্যাদি ।
এভাবে ১ থেকে ১০০ এর মধ্যে ৩৫ টি সংখ্যাকে দুইটি স্বাভাবিক সংখ্যার বর্গের যোগফল হিসেবে প্রকাশ করা যায়। আবার কিছু স্বাভাবিক সংখ্যাকে দুই বা ততোধিক উপায়ে দুইটি স্বাভাবিক সংখ্যার বর্গের সমষ্টিরূপে প্রকাশ করা যায় । যেমন,
৫০ = ১^২ + ৭^২ = ৫^২ + ৫^২
৬৫ = ১^২ + ৮^২ = ৪^২ + ৭^২
