সমতলক্ষেত্রের ক্ষেত্রফল

আজকে আমাদের আলোচনার বিষয়ঃ সমতলক্ষেত্রের ক্ষেত্রফল। এটি নবম – দশম শ্রেনী গণিতের ক্ষেত্রফল সম্পর্কিত উপপাদ্য ও সম্পাদ্য এর অন্তর্গত।

 

 

সমতলক্ষেত্রের ক্ষেত্রফল

প্রত্যেক সীমাবদ্ধ সমতলক্ষেত্রের নির্দিষ্ট ক্ষেত্রফল রয়েছে। এই ক্ষেত্রফল পরিমাপের জন্য সাধারণত এক একক বাহু বিশিষ্ট বর্গক্ষেত্রের ক্ষেত্রফলকে বর্গ একক হিসেবে গ্রহণ করা হয়। যেমন, যে বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য এক সেন্টিমিটার তার ক্ষেত্রফল হবে এক বর্গসেন্টিমিটার।

আমরা জানি,

ক) ABCD আয়তক্ষেত্রের দৈর্ঘ্য AB = a একক (যথা: মিটার), প্রস্থ BC = b একক (যথা: মিটার) হলে, ABCD আয়তক্ষেত্রের ক্ষেত্রফল ab বর্গ একক = (যথা: বর্গমিটার)।

খ) ABCD বর্গক্ষেত্রের বাহুর দৈর্ঘ্য : (যথা: মিটার) হলে, = a একক ABCD বর্গক্ষেত্রের ক্ষেত্রফল = a2 বর্গ একক = (যথা: বর্গমিটার)।

দুইটি ক্ষেত্রের ক্ষেত্রফল সমান হলে এদের মধ্যে = চিহ্ন ব্যবহার করা হয়। যেমন, ABCD আয়তক্ষেত্রের ক্ষেত্রফল AED = ত্রিভুজক্ষেত্রের ক্ষেত্রফল, যেখানে AB = BE

উল্লেখ্য যে, ∆ABC ও ∆DEF সর্বসম হলে, ∆ABC ≌ ∆DEF লেখা হয়। এ ক্ষেত্রে অবশ্যই ∆ABC এর ক্ষেত্রফল = ∆DEF এর ক্ষেত্রফল।

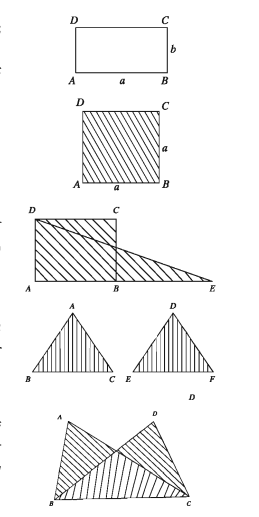
কিন্তু দুইটি ত্রিভুজক্ষেত্রের ক্ষেত্রফল সমান হলেই ত্রিভুজ দুইটি সর্বসম হয় না। যেমন, চিত্রে ∆ABC এর ক্ষেত্রফল = ∆DBC এর ক্ষেত্রফল। কিন্তু ∆ABC ও ∆DBC সর্বসম নয় ।

 

 

উপপাদ্য ৩৬.

একই ভূমির উপর এবং একই সমান্তরাল রেখাযুগলের মধ্যে অবস্থিত সকল ত্রিভুজক্ষেত্রের ক্ষেত্রফল সমান ।

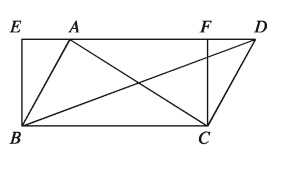
মনে করি, ABC ও DBC ত্রিভুজদ্বয় একই ভূমি BC এর উপর এবং একই সমান্তরাল রেখাযুগল BC ও AD এর মধ্যে অবস্থিত।

প্রমাণ করতে হবে যে, ∆ABC এর ক্ষেত্রফল = ∆DBC এর ক্ষেত্রফল।

 

 

অঙ্কন:

BC রেখাংশের B ও C বিন্দুতে যথাক্রমে BE ও CF লম্ব আঁকি, যা DA এর বর্ধিতাংশকে E বিন্দুতে এবং AD রেখাকে F বিন্দুতে ছেদ করে। ফলে EBCF একটি আয়তক্ষেত্র তৈরি হয়।

প্রমাণ:

∆ABC এর ভূমি BC এবং উচ্চতা BE

∆ABC এর ক্ষেত্রফল = 1/2 x BC x  BE …….(i)

আবার, ∆DBC এর ভূমি BC এবং উচ্চতা CF

:: ∆DBC এর ক্ষেত্রফল = 1/2 × BC x CF = 1/2 x BC X BE …….(ii); [EBCF আয়তক্ষেত্র |

(i) ও (ii) নং তুলনা করে পাই, ∆ABC এর ক্ষেত্রফল = ∆DBC এর ক্ষেত্রফল। (প্রমাণিত)

অনুসিদ্ধান্ত ১.

একই ভূমির একই পাশে অবস্থিত সকল ত্রিভুজক্ষেত্রের ক্ষেত্রফল সমান হলে, এরা একই সমান্তরাল রেখায়ুপলের মধ্যে অবস্থিত হবে।

অনুসিদ্ধান্ত ২.

কোনো ত্রিভুজ ও সামান্তরিক একই ভূমি ও একই সমান্তরাল রেখাযুগলের মধ্যে অবস্থিত হলে, ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক।

 

 

ইঙ্গিত:

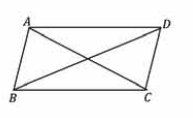
চিত্রে, ABCD সামান্তরিক। AC কর্ণ।

∆ABC = ∆ADC

∆ABC = সামাঙ্করিক ABCD

উপপাদ্য ৩৭.

একই ভূমির উপর এবং একই সমান্তরাল রেখাযুগলের মধ্যে অবস্থিত সামান্তরিকক্ষেত্রসমূহের ক্ষেত্রফল সমান।

 

 

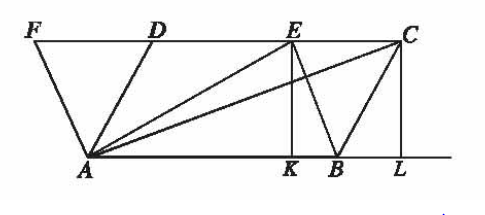
চিত্রে, ABCD ও ABEF সামান্তরিকক্ষেত্র দুইটি একই ভূমি AB এর উপর এবং একই সমান্তরাল রেখাযুগল AB ও PC এর মধ্যে অবস্থিত।

প্রমাণ করতে হবে যে, ABCD সামান্তরিকের ক্ষেত্রফল = ABEF সামান্তরিকের ক্ষেত্রফল।

অঙ্কন :

A, C ও A, E যোগ করি। C ও E বিন্দু থেকে ভূমি AB ও এর বর্ধিত রেখাংশের উপর EK ও CL লম্ব টানি।

প্রমাণ:

∆ABC এর ক্ষেত্রফল = 1/2 × AB × CL এবং

∆ABE এর ক্ষেত্রফল = 1/2 × AB × EK

যেহেতু CL = EK, [অঙ্কনানুসারে AL || FC]

অতএব, ∆ABC এর ক্ষেত্রফল = ∆ABE এর ক্ষেত্রফল

সামান্তরিকক্ষেত্র ABCD এর ক্ষেত্রফল = সামান্তরিকক্ষেত্র ABEF এর ক্ষেত্রফল ।

:. ABCD সামান্তরিকের ক্ষেত্রফল = ABEF সামান্তরিকের ক্ষেত্রফল। (প্রমাণিত)

উপপাদ্য ৩৮. পিথাগোরাসের উপপাদ্য

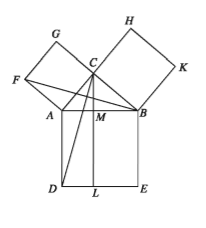
সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।

 

 

বিশেষ নির্বচন

মনে করি, ABC সমকোণী ত্রিভুজের ∠ACB সমকোণ এবং AB অতিভুজ।

প্রমাণ করতে হবে যে, AB2 = BC2 + AC2

অঙ্কন:

AB, AC এবং BC বাহুর উপর যথাক্রমে ABED, ACGF এবং BCHK বর্গক্ষেত্র অঙ্কন করি। C বিন্দু দিয়ে AD বা BE রেখার সমান্তরাল CL রেখা আঁকি। মনে করি, তা AB কে M বিন্দুতে এবং DE কে L বিন্দুতে ছেদ করে। C ও D এবং B ও F যোগ করি।

প্ৰমাণ :

ধাপ ১.

∆CAD ও ∆BAF তে CA = AF, AD = AB এবং অন্তর্ভুক্ত ∠CAD = ∠CAB + ∠BAD = ∠CAB + ∠CAF = অন্তর্ভুক্ত ∠BAF [∠BAD = ∠CAF = 1 সমকোণ]

অতএব, ∆CADE ≌ ∆BAF

ধাপ ২.

∆CAD এবং আয়তক্ষেত্র ADLM একই ভূমি AD এর উপর এবং AD ও CL সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত। সুতরাং আয়তক্ষেত্র ADLM = 2 ∆CAD [উপপাদ্য ৩৭]

ধাপ ৩.

∆BAF এবং বর্গক্ষেত্র ACGF একই ভূমি AF এর উপর এবং AF ও BG সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত।
সুতরাং বর্গক্ষেত্র ACGF = 2 ∆FAB = 2 ∆CAD [উপপাদ্য ৩৭]

ধাপ ৪.

আয়তক্ষেত্র ADLM = বর্গক্ষেত্র ACGF

ধাপ ৫.

অনুরূপভাবে C, E ওA, K যোগ করে প্রমাণ করা যায় যে, আয়তক্ষেত্র BELM = বর্গক্ষেত্র BCHK

ধাপ ৬.

আয়তক্ষেত্র (ADLM + BELM) = বর্গক্ষেত্র ACGF + বর্গক্ষেত্র BCHK বা, বর্গক্ষেত্র ABED = বর্গক্ষেত্র ACGF + বর্গক্ষেত্র BCHK অর্থাৎ, AB2 = BC2 + AC2 (প্রমাণিত)

সম্পাদ্য ১৩.

এমন একটি সামান্তরিক আঁকতে হবে, যার একটি কোণ একটি নির্দিষ্ট কোণের সমান এবং যা দ্বারা সীমাবদ্ধ ক্ষেত্র একটি ত্রিভুজক্ষেত্রের ক্ষেত্রফলের সমান।

 

 

মনে করি, ABC একটি নির্দিষ্ট ত্রিভুজক্ষেত্র এবং ∠x একটি নির্দিষ্ট কোণ। এরূপ সামান্তরিক আঁকতে হবে, যার একটি কোণ ∠x এর সমান এবং যা দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল ∆ABC এর ক্ষেত্রফলের সমান।

অঙ্কন:

BC বাহুকে E বিন্দুতে সমদ্বিখণ্ডিত করি। EC রেখাংশের E বিন্দুতে ∠x এর সমান ∠CEF আঁকি। A বিন্দু দিয়ে BC বাহুর সমান্তরাল AG রশ্মি টানি এবং মনে করি তা EF রশ্মিকে F’ বিন্দুতে ছেদ করে। C বিন্দু দিয়ে EF রেখাংশের সমান্তরাল CG রশ্মি টানি এবং মনে করি তা AG রশ্মিকে G বিন্দুতে ছেদ করে। তাহলে, ECGF ই উদ্দিষ্ট সামান্তরিক।

প্রমাণ:

A, E যোগ করি।

এখন, ∆ABE এর ক্ষেত্রফল = ∆AEC এর ক্ষেত্রফল [যেহেতু ভূমি BE = ভূমি EC এবং উভয়ের একই উচ্চতা ]

∆ABC এর ক্ষেত্রফল = 2 ∆AEC এর ক্ষেত্রফল

আবার, সামান্তরিক ক্ষেত্র ECGF এর ক্ষেত্রফল 2 ∆AEC এর ক্ষেত্রফল [যেহেতু, উভয়ে একই = ভূমি EC এর উপর অবস্থিত এবং EC || AG]

সামান্তরিক ক্ষেত্র ECGF এর ক্ষেত্রফল = ∆ABC এর ক্ষেত্রফল আবার, ∠CEF = ∠r [যেহেতু EF || CG, অঙ্কন অনুসারে] সামান্তরিক ECGF ই নির্ণেয় সামান্তরিক।

সম্পাদ্য ১৪.

এমন একটি ত্রিভুজ আঁকতে হবে যা দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল একটি নির্দিষ্ট চতুর্ভুজক্ষেত্রের ক্ষেত্রফলের সমান।

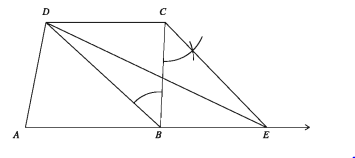
মনে করি, ABCD একটি চতুর্ভুজক্ষেত্র। এরূপ একটি ত্রিভুজ আঁকতে হবে যা দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল ABCD চতুর্ভুজক্ষেত্রের ক্ষেত্রফলের সমান।

 

 

অঙ্কন:

D, B যোগ করি। C বিন্দু দিয়ে CE || DB টানি। মনে করি, তা AB বাহুর বর্ধিতাংশকে দ্র বিন্দুতে ছেদ করে। D, E যোগ করি। তাহলে, ADAE ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ:

BD ভূমির উপর ∆BDC ও ∆BDE অবস্থিত এবং DB || CE [অঙ্কন অনুসারে]

∆BDC এর ক্ষেত্রফল = ∆BDE এর ক্ষেত্রফল

∆BDC এর ক্ষেত্রফল + ∆ABD এর ক্ষেত্রফল = ∆BDE এর ক্ষেত্রফল + ∆ABD এর ক্ষেত্রফল

চতুর্ভুজক্ষেত্র ABCD এর ক্ষেত্রফল ∆ADE এর ক্ষেত্রফল

অতএব, ∆ADE ই নির্ণেয় ত্রিভুজ।

বিশেষ দ্রষ্টব্য:

উপরের পদ্ধতির সাহায্যে নির্দিষ্ট চতুর্ভুজক্ষেত্রের ক্ষেত্রফলের সমান ক্ষেত্রফল বিশিষ্ট অসংখ্য ত্রিভুজক্ষেত্র আঁকা যাবে।

সম্পাদ্য ১৫.

এমন একটি সামান্তরিক আঁকতে হবে যার একটি কোণ দেওয়া আছে এবং তা দ্বারা সীমাবদ্ধ ক্ষেত্র একটি নির্দিষ্ট চতুর্ভুজক্ষেত্রের ক্ষেত্রফলের সমান।

মনে করি, ABCD একটি নির্দিষ্ট চতুর্ভুজক্ষেত্র এবং ∠x একটি নির্দিষ্ট কোণ। এরূপ একটি সামান্তরিক আঁকতে হবে যার একটি কোণ প্রদত্ত ∠x এর সমান এবং সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল ABCD ক্ষেত্রের ক্ষেত্রফলের সমান ।

 

 

অঙ্কন:

B, D যোগ করি। C বিন্দু দিয়ে CF || DB টানি এবং মনে করি, CF, AB বাহুর বর্ধিতাংশকে F’ বিন্দুতে ছেদ করে। AF রেখাংশের মধ্যবিন্দু G নির্ণয় করি। AG রেখাংশের A বিন্দুতে ∠x এর সমান ∠GAK আঁকি এবং G বিন্দু দিয়ে GH || AK টানি। D বিন্দু দিয়ে KDH || AG টানি এবং মনে করি, তা AK ও GH কে যথাক্রমে K ও H বিন্দুতে ছেদ করে। তাহলে, AGHK ই উদ্দিষ্ট সামান্তরিক।

প্রমাণ:

D, F যোগ করি। AGHK একটি সামান্তরিক [অঙ্কন অনুসারে]

যেখানে, ∠GAK =  ∠x। আবার, ∠DAF এর ক্ষেত্রফল চতুর্ভুজক্ষেত্র ABCD এর ক্ষেত্রফল এবং সামান্তরিক ক্ষেত্র AGHK এর ক্ষেত্রফল = ∠DAF এর ক্ষেত্রফল।

অতএব, AGHK ই নির্ণেয় সামান্তরিক।