আজকে আমাদের আলোচনার বিষয়ঃ সমান্তরাল সরলরেখা। এটি নবম – দশম শ্রেনী গণিতের রেখা, কোণ ও ত্রিভুজ এর অন্তর্গত।

সমান্তরাল সরলরেখা ( Parallel Straight Lines)
একান্তর কোণ, অনুরূপ কোণ, ছেদকের একই পার্শ্বস্থ অন্তঃস্থ কোণ (Alternate angle, Corresponding angle, Co-interior angle)
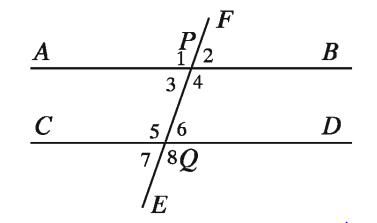
উপরের চিত্রে, AB ও CD দুইটি সরলরেখা এবং EF সরলরেখা এদেরকে P ও Q বিন্দুতে ছেদ করেছে। EF সরলরেখা AB ও CD সরলরেখাদ্বয়ের ছেদক। ছেদকটি AB ও CD সরলরেখা দুইটির সাথে ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8 মোট আটটি কোণ তৈরি করেছে। এ কোণগুলোর মধ্যে
ক) ∠1 এবং ∠5, ∠2 এবং ∠6, ∠3 এবং ∠7, ∠4 এবং ∠8 পরস্পর অনুরূপ কোণ।
খ) ∠3 এবং ∠6, ∠4 এবং ∠5 হলো পরস্পর একান্তর কোণ
গ) ∠4, ∠6 ডানপাশের অন্তঃস্থ কোণ ।
ঘ) ∠3, ∠5 বামপাশের অন্তঃস্থ কোণ ।
সমতলে দুইটি সরলরেখা পরস্পরকে ছেদ করতে পারে অথবা তারা সমান্তরাল। সরলরেখাদ্বয় পরস্পরছেদী হয়, যদি উভয়রেখায় অবস্থিত একটি সাধারণ বিন্দু থাকে। অন্যথায় সরলরেখা দুইটি সমান্তরাল। লক্ষণীয় যে, দুইটি ভিন্ন সরলরেখার সর্বাধিক একটি সাধারণ বিন্দু থাকতে পারে।

একই সমতলে অবস্থিত দুইটি সরলরেখার সমান্তরালতা নিম্নে বর্ণিত তিনভাবে সংজ্ঞায়িত করা যায়:
ক) সরলরেখা দুইটি কখনও পরস্পরকে ছেদ করে না (দুই দিকে অসীম পর্যন্ত বর্ধিত করা হলেও)।
খ) একটি সরলরেখার প্রতিটি বিন্দু অপরটি থেকে সমান ক্ষুদ্রতম দূরত্বে অবস্থান করে।
গ) সরলরেখা দুইটিকে অপর একটি সরলরেখা ছেদ করলে উৎপন্ন একান্তর কোণ বা অনুরূপ কোণগুলো সমান হয় ।
সংজ্ঞা ক অনুসারে একই সমতলে অবস্থিত দুইটি সরলরেখা একে অপরকে ছেদ না করলে সেগুলো সমান্তরাল। দুইটি সমান্তরাল সরলরেখা থেকে যেকোনো দুইটি রেখাংশ নিলে, রেখাংশ দুইটিও পরস্পর সমান্তরাল হয়।
সংজ্ঞা খ অনুসারে দুইটি সমান্তরাল সরলরেখার একটির যেকোনো বিন্দু থেকে অপরটির লম্ব-দূরত্ব সর্বদা সমান। লম্ব-দূরত্ব বলতে এদের একটির যেকোনো বিন্দু হতে অপরটির উপর অঙ্কিত লম্বের দৈর্ঘ্যকেই বুঝায়। আবার বিপরীতভাবে, দুইটি সরলরেখার একটির যেকোনো দুইটি বিন্দু থেকে অপরটির লম্ব-দূরত্ব পরস্পর সমান হলেও রেখাদ্বয় সমান্তরাল। এই লম্ব-দূরত্বকে দুইটি সমান্তরাল রেখাদ্বয়ের দূরত্ব বলা হয়।
সংজ্ঞা গ ইউক্লিডের পঞ্চম স্বীকার্যের সমতুল্য। জ্যামিতিক প্রমাণ ও অঙ্কনের জন্য এ সংজ্ঞাটি অধিকতর উপযোগী।
লক্ষ করি, কোনো নির্দিষ্ট সরলরেখার উপর অবস্থিত নয় এরূপ বিন্দুর মধ্য দিয়ে ঐ সরলরেখার সমান্তরাল করে একটি মাত্র সরলরেখা আঁকা যায়।
উপপাদ্য ৩.
দুইটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন
ক) প্রত্যেক অনুরূপ কোণ জোড়া সমান হবে ।
খ) প্রত্যেক একান্তর কোণ জোড়া সমান হবে।
গ) ছেদকের একই পাশের অন্তঃস্থ কোণ দুইটি পরস্পর সম্পূরক।
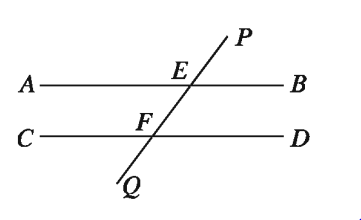
চিত্রে, AB || CD এবং PQ ছেদক এদের যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।
সুতরাং,
ক) ∠PEB = অনুরূপ ∠EFD [সংজ্ঞানুসারে]
খ) ∠AEF = একান্তর ∠EFD
গ) ∠BEF + ∠EFD = দুই সমকোণ।
উপপাদ্য ৪.
দুইটি সরলরেখা অপর একটি সরলরেখাকে ছেদ করলে যদি
ক) অনুরূপ কোণগুলো পরস্পর সমান হয়, অথবা
খ) একান্তর কোণগুলো পরস্পর সমান হয়, অথবা
গ) ছেদকের একই পাশের অন্তঃস্থ কোণদ্বয়ের যোগফল দুই সমকোণের সমান হয়, তবে ঐ সরলরেখা দুইটি পরস্পর সমান্তরাল।
চিত্রে, AB ও CD রেখাদ্বয়কে PQ রেখা যথাক্রমে E ও F বিন্দুতে ছেদ করেছে এবং
ক) ∠PEB = অনুরূপ ∠EFD অথবা,
খ) ∠AEF = একান্তর ∠EFD অথবা,
গ) ∠BEF + ∠EFD = দুই সমকোণ ।
সুতরাং, AB ও CD রেখা দুইটি পরস্পর সমান্তরাল।

অনুসিদ্ধান্ত ১.
যেসব সরলরেখা একই সরলরেখার সমান্তরাল সেগুলো পরস্পর সমান্তরাল।
অনুশীলনী
১. কোণের অভ্যন্তর ও বহির্ভাগের সংজ্ঞা দাও ।
২. যদি একই সরলরেখাস্থ তিনটি ভিন্ন বিন্দু হয়, তবে চিত্রের উৎপন্ন কোণগুলোর নামকরণ কর।
৩. সন্নিহিত কোণের সংজ্ঞা দাও এবং এর বাহুগুলো চিহ্নিত কর।
৪. চিত্রসহ সংজ্ঞা দাও: বিপ্রতীপ কোণ, পূরক কোণ, সম্পূরক কোণ, সমকোণ, সূক্ষ্মকোণ এবং স্থূলকোণ
