আজকে আমাদের আলোচনার বিষয়ঃ সম্পাদ্যে চতুর্ভুজ অঙ্কন । এটি অষ্টম শ্রেনী গণিতের চতুর্ভুজ এর অন্তর্গত।

সম্পাদ্যে চতুর্ভুজ অঙ্কন
পূর্ববর্তী শ্রেণিতে আমরা জেনেছি, ত্রিভুজের তিনটি বাহু দেওয়া থাকলে নির্দিষ্ট ত্রিভুজ আঁকা যায় । কিন্তু চতুর্ভুজের চারটি বাহু দেওয়া থাকলে নির্দিষ্ট কোনো চতুর্ভুজ আঁকা যায় না । চতুর্ভুজ অঙ্কনের জন্য আরও উপাত্তের প্রয়োজন । চতুর্ভুজের চারটি বাহু, চারটি কোণ ও দুইটি কর্ণ, এই মোট দশটি উপাত্ত আছে । একটি চতুর্ভুজ আঁকতে পাঁচটি অনন্য নিরপেক্ষ উপাত্তের প্রয়োজন । যেমন, কোনো চতুর্ভুজের চারটি বাহু ও একটি নির্দিষ্ট কোণ দেওয়া থাকলে, চতুর্ভুজ আঁকা যাবে ।
নিম্নোক্ত পাঁচটি উপাত্ত জানা থাকলে, নির্দিষ্ট চতুর্ভুজ আঁকা যায় ।
(ক) চারটি বাহু ও একটি কোণ
(খ) চারটি বাহু ও একটি কর্ণ
(গ) তিনটি বাহু ও দুইটি কর্ণ
(ঘ) তিনটি বাহু ও এদের অন্তর্ভুক্ত দুইটি কোণ
(ঙ) দুইটি বাহু ও তিনটি কোণ ।
অনেক সময় কম উপাত্ত দেওয়া থাকলেও বিশেষ চতুর্ভুজ আঁকা যায় । এক্ষেত্রে যুক্তি দ্বারা পাঁচটি উপাত্ত পাওয়া যায় ।
- একটি বাহু দেওয়া থাকলে, বর্গ আঁকা যায় । এখানে চারটি বাহুই সমান এবং একটি কোণ সমকোণ ।
- দুইটি সন্নিহিত বাহু দেওয়া থাকলে, আয়ত আঁকা যায় । এখানে বিপরীত বাহু দুইটি পরস্পর সমান এবং একটি কোণ সমকোণ ।
- একটি বাহু এবং একটি কোণ দেওয়া থাকলে, রম্বস আঁকা যায় । এখানে চারটি বাহুই সমান ।
- দুইটি সন্নিহিত বাহু এবং এদের অন্তর্ভুক্ত কোণ দেওয়া থাকলে, সামান্তরিক আঁকা যায় । এখানে বিপরীত বাহু দুইটি পরস্পর সমান ও সমান্তরাল ।
সম্পাদ্য ১
কোনো চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য ও একটি কোণ দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
মনে করি, একটি চতুর্ভুজের চার বাহুর দৈর্ঘ্য a,b,c,d এবং a ও b বাহুদ্বয়ের অন্তর্ভুক্ত কোণ ∠x দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
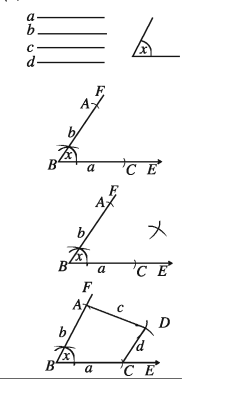
অঙ্কনের বিবরণ :
(১) যেকোনো রশ্মি BE থেকে_BC = a নিই । B বিন্দুতে ∠EBF = ∠x আঁকি ।
(২) BF থেকে BA = b নিই । A ও C কে কেন্দ্র করে যথাক্রমে c ও d এর সমান ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি । এরা পরস্পর D বিন্দুতে ছেদ করে ।
(৩) A ও D এবং C ও D যোগ করি ।
তাহলে, ABCD ই উদ্দিষ্ট চতুৰ্ভুজ ।
প্রমাণ :
অঙ্কন অনুসারে,
AB = b, BC = a, AD = c, DC = d এবং ∠ABC = ∠x
ABCD ই নির্ণেয় চতুৰ্ভুজ ।
সম্পাদ্য ২
কোনো চতুর্ভুজের চারটি বাহু ও একটি কর্ণের দৈর্ঘ্য দেওয়া আছে। চতুর্ভুজটি আঁকতে হবে ।
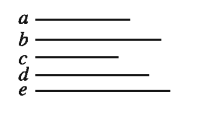
মনে করি, একটি চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য a, b, c, d এবং একটি কর্ণের দৈর্ঘ্য e দেওয়া আছে, যেখানে a + b >e এবং c + d>e চতুর্ভুজটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
(১) যেকোনো রশ্মি BE থেকে BD = e নিই । B ও D কে কেন্দ্র করে যথাক্রমে a ও b এর সমান ব্যাসার্ধ নিয়ে BD এর একই পাশে
দুইটি বৃত্তচাপ আঁকি । বৃত্তচাপদ্বয় A বিন্দুতে ছেদ করে ।
(২) আবার, B ও D কে কেন্দ্র করে যথাক্রমে d ও c এর সমান ব্যাসার্ধ নিয়ে BD এর যেদিকে A আছে তার বিপরীত দিকে আরও দুইটি বৃত্তচাপ আঁকি । এই বৃত্তচাপদ্বয় পরস্পর C বিন্দুতে ছেদ করে ।
(৩) A ও B, A ও D, B ও C এবং C ও D যোগ করি । তাহলে, ABCD ই উদ্দিষ্ট চতুৰ্ভুজ ।
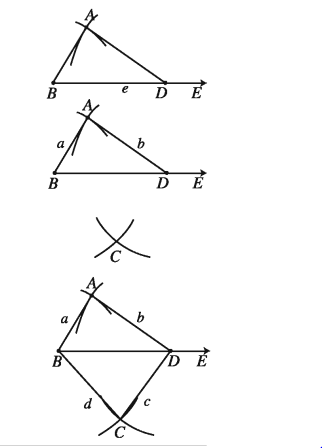
প্রমাণ :
অঙ্কন অনুসারে, AB = a, AD = b, BC = d, CD = c এবং কর্ণ BD = e
সুতরাং, ABCD ই নির্ণেয় চতুৰ্ভুজ ।
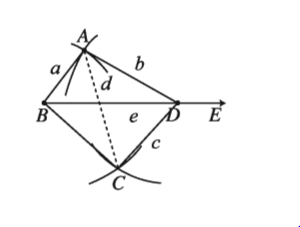
সম্পাদ্য ৩
কোনো চতুর্ভুজের তিনটি বাহু ও দুইটি কর্ণের দৈর্ঘ্য দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
মনে করি, একটি চতুর্ভুজের তিনটি বাহুর দৈর্ঘ্য a,b,c এবং দুইটি কর্ণের দৈর্ঘ্য d,e দেওয়া আছে, যেখানে a+b>e । চতুর্ভুজটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
(১) যেকোনো রশ্মি BE থেকে BD = e নিই । B ও D কে কেন্দ্ৰ করে যথাক্রমে a ও b এর সমান ব্যাসার্ধ নিয়ে BD এর একই পাশে দুইটি বৃত্তচাপ আঁকি । বৃত্তচাপদ্বয় A বিন্দুতে ছেদ করে ।
(২) আবার, D ও A কে কেন্দ্র করে যথাক্রমে c ও d এর সমান ব্যাসার্ধ নিয়ে BD এর যেদিকে এ রয়েছে এর বিপরীত দিকে আরও দুইটি বৃত্তচাপ আঁকি । এই বৃত্তচাপদ্বয় পরস্পরকে C বিন্দুতে ছেদ করে ।
(৩) A ও B, A ও D, B ও C এবং C ও D যোগ করি । তাহলে, ABCD ই উদ্দিষ্ট চতুৰ্ভুজ ।
প্রমাণ :
অঙ্কন অনুসারে, AB = a, AD = b, CD = c এবং কর্ণ BD = e ও AC = d
সুতরাং, ABCD ই নির্ণেয় চতুৰ্ভুজ ।
সম্পাদ্য ৪
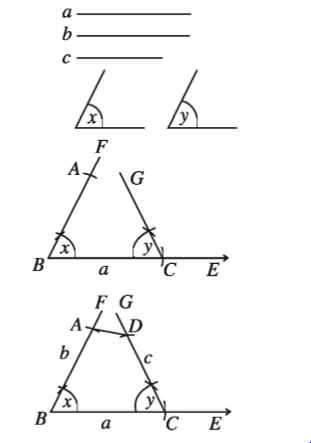
কোনো চতুর্ভুজের তিনটি বাহুর দৈর্ঘ্য ও দুইটি অন্তর্ভুক্ত কোণ দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
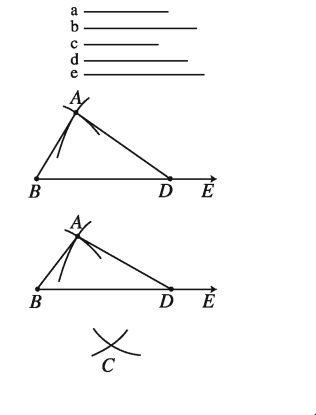
মনে করি, একটি চতুর্ভুজের তিনটি বাহু a,b,c এবং a ও b বাহুর অন্তর্ভুক্ত কোণ ∠x এবং a ও c বাহুর অন্তর্ভুক্ত কোণ ∠y দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
যেকোনো রশ্মি BE থেকে BC = a নিই ।
B ও C বিন্দুতে ∠x ও ∠y এর সমান করে যথাক্রমে ∠CBF ও ∠BCG অঙ্কন করি। BF থেকে BA = b এবং CG থেকে CD = c নিই । A,D যোগ করি ।
তাহলে, ABCD ই উদ্দিষ্ট চতুৰ্ভুজ ।
প্রমাণ :
অঙ্কন অনুসারে, AB = b, BC = a, CD=c,
∠ABC = ∠x ও ∠BCD = ∠y
সুতরাং ABCD ই নির্ণেয় চতুৰ্ভুজ ।
সম্পাদ্য ৫
কোনো চতুর্ভুজের দুইটি সন্নিহিত বাহুর দৈর্ঘ্য ও তিনটি কোণ দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে । মনে করি, একটি চতুর্ভুজের দুইটি সন্নিহিত বাহু a, b এবং তিনটি কোণ ∠x,∠y,∠z দেওয়া আছে । চতুর্ভুজটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
যেকোনো রশ্মি BE থেকে BC = a নিই । B ও C বিন্দুতে ∠x ও ∠y এর সমান করে যথাক্রমে ∠CBF ও ∠BCG অঙ্কন করি। BF থেকে BA= b নিই । A বিন্দুতে ∠z এর সমান করে ∠BAH অঙ্কন করি । AH ও CG পরস্পরকে D বিন্দুতে ছেদ করে ।
তাহলে, ABCD ই উদ্দিষ্ট চতুৰ্ভুজ ।
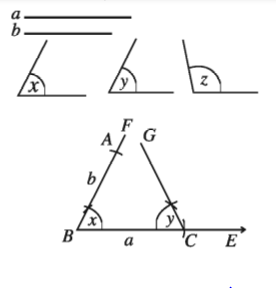
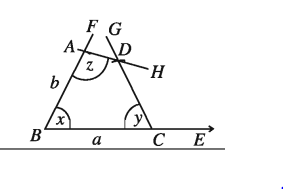
প্রমাণ :
অঙ্কন অনুসারে, AB = b, BC = a, ∠ABC = ∠x ∠DCB = ∠y ও ∠BAD = ∠z সুতরাং ABCD ই নির্ণেয় চতুৰ্ভুজ ।
সম্পাদ্য ৬
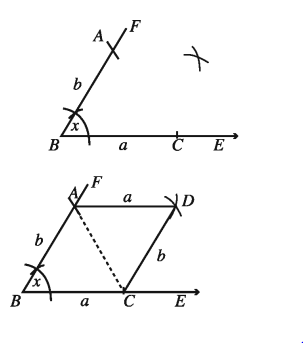
কোনো সামান্তরিকের সন্নিহিত দুইটি বাহুর দৈর্ঘ্য এবং বাহুদ্বয়ের অন্তর্ভুক্ত কোণ দেওয়া আছে ৷ সামান্তরিকটি আঁকতে হবে ।
মনে করি, একটি সামান্তরিকের দুইটি সন্নিহিত বাহু a ও b এবং a এদের অন্তর্ভুক্ত কোণ ∠x দেওয়া আছে । সামান্তরিকটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
যেকোনো রশ্মি BE থেকে BC = a নিই B বিন্দুতে ∠EBF = ∠x অঙ্কন করি । BF থেকে b এর সমান BA নিই । A ও C বিন্দুকে কেন্দ্র করে যথাক্রমে a ও b এর সমান ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি । এরা পরস্পরকে D বিন্দুতে ছেদ করে । A, D ও C, D যোগ করি । তাহলে, ABCD ই উদ্দিষ্ট সামান্তরিক ।
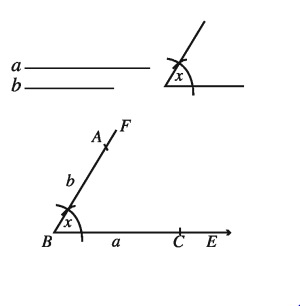
প্রমাণ :
A,C যোগ করি । ∆ABC ও ∆ADC এ
AB = CD = b,
AD = BC = a এবং AC বাহু সাধারণ ।
∆ABC ≌ ∆ADC
অতএব, ∠BAC = ∠DCA। কিন্তু, কোণ দুইটি একান্তর কোণ ।
AB || CD
অনুরূপভাবে, প্রমাণ করা যায় যে, BC || AD
সুতরাং ABCD একটি সামান্তরিক ।
আবার অঙ্কন অনুসারে ∠ABC = ∠x
অতএব, ABCD ই নির্ণেয় সামান্তরিক ।
সম্পাদ্য ৭
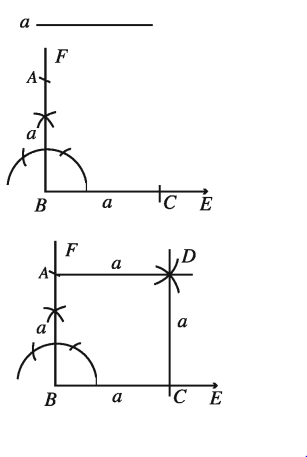
কোনো বর্গের একটি বাহুর দৈর্ঘ্য দেওয়া আছে, বর্গটি আঁকতে হবে ।
মনে করি, a কোনো বর্গের একটি বাহুর দৈর্ঘ্য । বর্গটি আঁকতে হবে ।
অঙ্কনের বিবরণ :
যেকোনো রশ্মি BE থেকে BC = a নিই ।
B বিন্দুতে BF || BC আঁকি ।
BF থেকে BA = a নিই। A ও C কে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি । বৃত্তচাপদ্বয় পরস্পরকে D বিন্দুতে ছেদ করে । A ও D এবং C ও D যোগ করি ।
তাহলে, ABCD ই উদ্দিষ্ট বর্গ ।
প্রমাণ :
ABCD চতুর্ভুজের AB = BC = CD = DA = a এবং ∠ABC = এক সমকোণ ।
সুতরাং, এটি একটি বর্গ
অতএব, ABCD ই নির্ণেয় বর্গ ।
