আজকে আমরা নমুনাক্ষেত্র এবং Probability Tree দ্বারা সম্ভাবনা নির্ণয় আলোচনা করবো। যা উচ্চতর গণিতের সম্ভাবনা অংশের অন্তর্গত।

নমুনাক্ষেত্র এবং Probability Tree দ্বারা সম্ভাবনা নির্ণয়
আগেই বলা হয়েছে, কোনো পরীক্ষায় সম্ভাব্য ফলাফলগুলো নিয়ে যে ক্ষেত্র তৈরি হয় তাকে নমুনাক্ষেত্র বলে। অনেক পরীক্ষায় নমুনাক্ষেত্রের আকার বেশ বড় হয়। এসব ক্ষেত্রে নমুনা বিন্দু গণনা করা ও নমুনাক্ষেত্র তৈরি করা সময় সাপেক্ষ এমন কি ভুল হওয়ার সম্ভাবনাও থাকে। সেক্ষেত্রে আমরা probability tree এর সাহায্যে নমুনাক্ষেত্র তৈরি করতে পারি ও বিভিন্ন ঘটনার সম্ভাবনাও বের করতে পারি।
উদাহরণ ৬.
মনে করি, দুইটি নিরপেক্ষ মুদ্রা একসাথে একবার নিক্ষেপ করা হলো। নমুনাক্ষেত্রটি তৈরি কর। প্রথম মুদ্রায় H এবং দ্বিতীয় মুদ্রায় T আসার সম্ভাবনা নির্ণয় কর।
সমাধান:
দুইটি মুদ্রা নিক্ষেপ পরীক্ষাকে দুই ধাপ হিসেবে বিবেচনা করা যায়। প্রথম ধাপে একটা মুদ্ৰা নিক্ষেপে 2 টি ফলাফল H অথবা T আসতে পারে। দ্বিতীয় ধাপে অপর মুদ্রা নিক্ষেপেও 2 টি ফলাফল H অথবা T আসতে পারে। পরীক্ষার মোট ফলাফলকে probability tree এর সাহায্যে নিম্নভাবে দেখানো হয়।
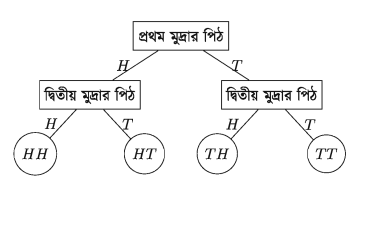
সম্ভাব্য নমুনা বিন্দুগুলো HH, HT, TH, TT। তাহলে নমুনাক্ষেত্রটি হবে {HH, HT, TH, TT} । 1 এখানে নমুনা বিন্দুর সংখ্যা 4 এবং প্রতিটি নমুনা বিন্দুর আসার সম্ভাবনা 1/4। তাই প্রথম মুদ্রায় H ও দ্বিতীয় মুদ্রায় T আসার সম্ভাবনা হবে, P(HT) = 1/4
উদাহরণ ৭.
মনে করি, তিনটি মুদ্রা একবার নিক্ষেপ করা হলো। তিনটি নিরপেক্ষ মুদ্রা একসাথে একবার নিক্ষেপ করা হলে, probability tree তৈরি করে নমুনাক্ষেত্রটি দেখাও এবং নিচের ঘটনাগুলোর সম্ভাবনা নির্ণয় কর।
ক) কেবল একটা টেল, খ) তিনটাই হেড, গ) কমপক্ষে একটা টেল পাওয়ার সম্ভাবনা বের কর।
সমাধান:
প্রথমে মুদ্রা তিনটিকে তিন ধাপ হিসেবে বিবেচনা করি এবং প্রতি ধাপে 2 টি ফলাফল H অথবা T আসতে পারে। মোট ফলাফলকে probability tree এর সাহায্যে নিম্নভাবে দেখানো যায়:

তাহলে নমুনাক্ষেত্রটি হবে: { HHH HHT, HTH, HTT, THH, THT, TTH, TTT}
এখানে মোট নমুনা বিন্দু ৪ টি এবং এদের যেকোন একটি ঘটনা ঘটার সম্ভাবনা 1/8
ক) একটি টেল পাওয়ার অনুকূল ঘটনাগুলো {THH, HHT, HTH} = 3 টি ।
∴ P(1T) = 3/8 (কেননা প্রতিটি নমুনা বিন্দুর ঘটার সম্ভাবনা 1/8)
খ) তিনটিই হেড (H) পাওয়ার অনুকূল ঘটনা {HHH} = 1 টি।
∴ P(HHH) = 1/8
গ) কমপক্ষে 1টি টেল (T) পাওয়ার অনুকূল ঘটনাগুলো HHH ছাড়া বাকি সবগুলো অর্থাৎ {HHT, HTH, HTT, THH, THT, TTH, TTT} = 7 টি।
∴ P [ কমপক্ষে 1T] = 7/8
উদাহরণ ৮.
একটি নিরপেক্ষ ছক্কা ও একটি মুদ্রা একবার নিক্ষেপ করা হলো। Probability tree তৈরি করে নমুনাক্ষেত্রটি লিখ। ছক্কায় 5 এবং মুদ্রায় H আসার সম্ভাবনা বের কর।
সমাধান:
একটি ছক্কা ও একটি মুদ্রা নিক্ষেপ পরীক্ষাকে দুই ধাপ হিসেবে বিবেচনা করি। প্রথম ধাপে ছক্কা নিক্ষেপে 6 টি ফলাফল {1, 2, 3, 4, 5, 6} আসতে পারে। দ্বিতীয় ধাপে মুদ্রা নিক্ষেপে 2 টি ফলাফল H অথবা T আসতে পারে। তাই পরীক্ষায় মোট ফলাফলকে probability tree এর সাহায্যে নিম্নভাবে দেখানো যাবে।

তাহলে নমুনাক্ষেত্রটি হবে: {1H,1T, 2H, 2T,3H, 3T, 4H, AT, 5H, 5T, 6H, 6T} ।
এখানে মোট নমুনা বিন্দু 12 টি।
∴ ছক্কায় 5 এবং মুদ্রায় H আসার সম্ভাবনা P(5H): = 1/12
উদাহরণ ৯.
একজন লোকের ঢাকা হতে খুলনায় বাসে যাওয়ার সম্ভাবনা 2/5 এবং খুলনা হতে রাজশাহী ট্রেনে যাওয়ার সম্ভাবনা 5/8 । লোকটি খুলনায় বাসে এবং রাজশাহী ট্রেনে না যাওয়ার সম্ভাবনা কত? 8 Probability tree ব্যবহার করে দেখাও।
সমাধান:
সম্ভাবনার মাধ্যমে probability tree হবে
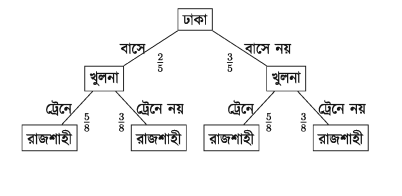
সুতরাং লোকটির খুলনায় বাসে এবং রাজশাহীতে ট্রেনে না যাওয়ার সম্ভাবনা
P[খুলনা বাস, রাজশাহী ট্রেনে নয়] = 2/5 x 3/8 = 6 /40 = 3 /20
