সরলরেখার ঢাল 

আজকে আমরা সরলরেখার ঢাল  সম্পর্কে  আলোচনা করবো  । যা উচ্চতর গণিতের  স্থানাঙ্ক জ্যামিতি অংশের অন্তর্গত।

 

 

সরলরেখার ঢাল

স্থানাঙ্ক জ্যামিতির এই অংশের প্রথমে আমরা সরলরেখার ঢাল বলতে কি বুঝায় এবং সরলরেখার ঢাল নির্ণয়ের কৌশল আলোচনা করবো। ঢালের ধারণা ব্যবহার করে একটি সরলরেখার বীজগাণিতিক রূপ কি হয় তা আলোচনা করা হবে। কোনো সরলরেখা দুইটি বিন্দু দিয়ে অতিক্রম করলে সেই সরলরেখার ঢালের প্রকৃতি ও উক্ত সরলরেখার সমীকরণ নির্ণয় করাই মূলত এই অংশের মূল আলোচনার বিষয়। দুইটি সরলরেখা কোনো বিন্দুতে মিলিত হলে বা ছেদ করলে সেই ছেদ বিন্দুর স্থানাঙ্ক নির্ণয়ের মাধ্যমে তিনটি সমীকরণ দ্বারা নির্দেশিত রেখার মাধ্যমে গঠিত ত্রিভুজ নিয়েও আলোচনা করা হবে। এখানে আমরা দেখাব বীজগণিতে দুই চলকের একঘাত সমীকরণ সরলরেখা নির্দেশ করে এবং তাদের সমাধান হলো সেই ছেদ বিন্দু।

 

 

ঢাল ( Gradient or slope )

পাশের চিত্রে AB সরলরেখাটি বিবেচনা করি। রেখাটি A (2, 3) ও B (6, 7 ) দুটি বিন্দু দিয়ে অতিক্রম করেছে। চিত্রানুসারে রেখাটি x অক্ষের ধনাত্মক দিকের সাথে ৪ কোণ উৎপন্ন করেছে। এই ৪ কোণ হলো x অক্ষের সাথে AB সরলরেখাটি কি পরিমাণ আনত হয়েছে তার পরিমাপ। স্থানাঙ্ক জ্যামিতিতে আমরা AB রেখার ঢাল (gradient) m কে নিম্নোক্ত ভাবে পরিমাপ করে থাকি :

m = y স্থানাঙ্কের পরিবর্তন /x স্থানাঙ্কের পরিবর্তন

= (7-3)/( 6 – 2) = 4 /4= 1

AB রেখার ঢাল, m = 1

 

 

সাধারণত, একটি সরলরেখা যখন A (x1,y1) ও B(x2, Y2) বিন্দু দিয়ে অতিক্রম করে তখন এর ঢাল (m) কে আমরা

m = (Y2 – Y1) /(X2 – X1). rise/ run = ওঠা /হাঁটা  দ্বারা প্রকাশ করে থাকি।

বাস্তবিকপক্ষে, কোনো সরলরেখা দ্বারা x অক্ষের ধনাত্মক দিকের সাথে উৎপন্ন কোণ ৪ এবং ঢাল m. এর মধ্যে সম্পর্ক হলো, m = tan8। উপরের চিত্রে AB রেখার ক্ষেত্রে সরলরেখার ঢাল m = 1 ‘, অর্থাৎ, tan 1 বা, 6 = 45° (একটি সূক্ষ্মকোণ)।

 

 

উদাহরণ ১৫.

নিম্নের প্রতিক্ষেত্রে নির্দেশিত বিন্দুদ্বয় দ্বারা অতিক্রান্ত সরলরেখার ঢাল নির্ণয় কর।

ক) A (2, 3) এবং B (3, 6)

খ) A’ ( 2, 1 ) এবং B’ (–1, 4 )

সমাধান:

ক) AB রেখার ঢাল = ওঠা /হাঁটা = (6-3)/( 3-2) =3/ 1 = 3

খ) A’B’ রেখার ঢাল = ওঠা /হাঁটা = (4-1)/ -1 – 2 = 3/-3 = -1

 

 

লক্ষণীয়:

উপরের চিত্র থেকে দেখা যাচ্ছে, AB রেখার ঢাল ধনাত্মক এবং উৎপন্ন কোণ একটি সূক্ষ্মকোণ। আবার, একই চিত্র থেকে এটি পরিষ্কার যে A’B’ রেখার ঢাল ঋণাত্মক এবং উৎপন্ন কোণ একটি স্থূলকোণ। সুতরাং উপরোক্ত আলোচনা থেকে আমরা এই সিদ্ধান্তে আসতে পারি যে, ঢাল ধনাত্মক হলে রেখা দ্বারা অক্ষের ধনাত্মক দিকের সাথে উৎপন্ন কোন সূক্ষ্মকোণ এবং ঢাল ঋণাত্মক হলে রেখা দ্বারা x অক্ষের ধনাত্মক দিকের সাথে উৎপন্ন কোণ একটি স্থূলকোণ।

উৎপন্ন কোণ শূন্য অথবা সমকোণ হলে ঢাল কি হবে তা নিম্নোক্ত উদাহরণের সাহায্যে ব্যাখ্যা করা হলো:

উদাহরণ ১৬.

A, B এবং C তিনটি বিন্দুর স্থানাঙ্ক যথাক্রমে (2, 2), (5, 2) এবং (2, 7)। কার্তেসীয় তলে AB ও AC রেখা অঙ্কন কর। সম্ভব হলে AB ও AC রেখার ঢাল নির্ণয় কর।

সমাধান:

কার্তেসীয় তলে AB ও AC রেখা অঙ্কন করা হলো।

 

 

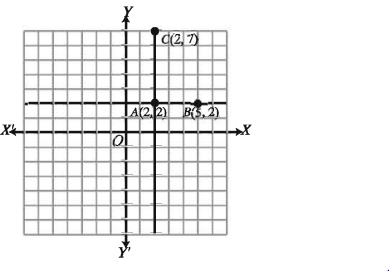
চিত্র থেকে দেখা যায় যে, AB রেখা x অক্ষের সমান্তরাল এবং AC রেখা য় অক্ষের সমান্তরাল।

AB রেখার ঢাল, m = (y2 – y1)/( X2 – X1) = (2-2)/(5-2) =0/3 = 0

AC রেখার ঢাল m = (y2 – y1)/( X2 – X1) সূত্র দ্বারা নির্ণয় করা যাবে না, কারণ x1 = X2 = 2 এবং x2 – X1 =2x2x1 = 01
যদি x1 = x2 হয় তবে রেখার ঢাল নির্ণয় করা যায় না কিন্তু রেখাটি y অক্ষের সমান্তরাল হয়।

সাধারণত কোনো সরলরেখা A ( x 1, y 1 ) ও B (2, y 2 ) বিন্দু দিয়ে অতিক্রম করলে

ঢাল, m = = (y2 – y1)/( X2 – X1)  বা, m = (y2 – y1)/( x1 – x2) যদি  x1 ≠ x2 হয়।

লক্ষ করি:

যদি x2 হয়, তাহলে রেখাটি y অক্ষের সমান্তরাল অর্থাৎ x অক্ষের উপর লম্ব হয়। X1 = এই রকম লম্ব রেখা বরাবর বা খাড়া রেখা বরাবর হাঁটা সম্ভব নয়। তাই ঢাল নির্ণয় করাও সম্ভব নয়।

মন্তব্য:

উপরের চিত্রে AB রেখার যেকোনো বিন্দুতে কোটি অর্থাৎ y = 2 এবং AC রেখার যেকোনো বিন্দুতে ভুজ r = 2। অর্থাৎ 2 তাই AB সরলরেখার সমীকরণ y = 2 এবং AC সরলরেখার সমীকরণ x = 2

উদাহরণ ১৭.

A(−3, 2) এবং B(3, – 2 ) বিন্দু দিয়ে অতিক্রমকারী রেখার ঢাল নির্ণয় কর।

সমাধান:

AB রেখার ঢাল m হলে,

= (y2 – y1)/( X2 – X1) = ওঠা /হাঁটা = {2-(-2)}/{-3-3} = 4/-6 = 2/-3

ঢাল ঋণাত্মক হওয়ায় রেখাটি অক্ষের ধনাত্মক দিকের সাথে স্থূলকোণ উৎপন্ন করেছে।

 

 

উদাহরণ ১৮.

A (1, − 1 ), B(2, 2 ) এবং C ( 4, t) বিন্দু তিনটি সমরেখ হলে t এর মান কত?

সমাধান:

সমরেখ হওয়ায় ABওBC রেখার ঢাল একই হবে।

সুতরাং আমরা পাই,

(2+1)/(2-1) = (t-2)/(4-2)

বা, 3/1 = (t-2)/2

বা, t – 2 = 6

বা, t = 8

সুতরাং t এর মান ৪

 

 

উদাহরণ ১৯.

A (t, 3t), B (t 2, 2t), C (t – 2, t) এবং D(1, 1) চারটি ভিন্ন বিন্দু। AB এবং CD রেখা সমান্তরাল হলে t এর সম্ভাব্য মান নির্ণয় কর।

সমাধান:

AB রেখার ঢাল m1 = (2t – 3t)/( t2 – t) =  -t/ t(t − 1) = 1/(1-t)

CD রেখার ঢাল m2 = (1- t )/(1-t+2) = (1-t)/( 3-t )

যেহেতু AB ও CD রেখা সমান্তরাল, AB ও CD রেখার ঢাল সমান অর্থাৎ, m1 = m2

বা,1/(1-t) = (1-t)/( 3-t )

বা, ( 1 – t) 2 = (3 – t)

বা, 1 – 2t + t2 = 3 – t

বা, t2 – t – 2 = 0

বা, t = −1 অথবা t = 2

সুতরাং t এর সম্ভাব্য মানসমূহ –1,2

 

 

অনুশীলনী

১. নিম্নের প্রতিটি ক্ষেত্রে A ও B বিন্দুগামী সরলরেখার ঢাল নির্ণয় কর।

ক) A ( 5, – 2 ) এবং B (2, 1 )

খ) A (3, 5 ) এবং B (–1, – 1 ) –

গ) A (t, t) এবং B (t 2, t)

ঘ) A(t, t + 1) এবং B (3t, 5t + 1 )

২. A (t, 1), B(2, 4) এবং C(1,t) তিনটি ভিন্ন বিন্দু সমরেখ হলে t এর মান নির্ণয় কর।

৩. দেখাও যে, A(0, − 3 ), B ( 4, – 2 ) এবং C (16, 1 ) বিন্দু তিনটি সমরেখ।

8. A(1, – 1), B(t, 2 ) এবং C (t 2, t + 3) সমরেখ হলে t এর সম্ভাব্য মান নির্ণয় কর।

৫. A (3, 3p) এবং B ( 4, p2 + 1 ) বিন্দুগামী রেখার ঢাল – 1 হলে p এর মান নির্ণয় কর।

৬. প্রমাণ কর যে, A (a, 0 ), B (0, b) এবং C(1, 1) সমরেখ হবে, যদি 1/a  +1/b = 1 হয়।

৭. A ( a, b ), B (b, a) এবং C (1) সমরেখ হলে প্রমাণ কর যে, a + b = 1

আরও দেখুনঃ

• ফাংশনের লেখচিত্র