দুই চলকবিশিষ্ট সরল একঘাত অসমতা

আজকে আমরা  সরল একঘাত অসমতা সম্পর্কে  আলোচনা করবো । যা উচ্চতর গণিতের সমীকরণ অংশের অন্তর্গত।

 

 

দুই চলকবিশিষ্ট সরল একঘাত অসমতা

আমরা দুই চলকবিশিষ্ট y = me + c (যার সাধারণ আকার ax + by + c = 0) আকারের সরল সমীকরণের লেখচিত্র অঙ্কন করতে শিখেছি (অষ্টম ও নবম-দশম শ্রেণিতে)। আমরা দেখেছি যে, এ রকম প্রত্যেক লেখচিত্রই একটি সরলরেখা। স্থানাঙ্কায়িত XY সমতলে ax+by+ c = 0 সমীকরণের লেখচিত্রের যেকোনো বিন্দুর স্থানাঙ্ক সমীকরণটিকে সিদ্ধ করে অর্থাৎ সমীকরণটির বামপক্ষে x ও y এর পরিবর্তে যথাক্রমে ঐ বিন্দুর ভুজ ও কোটি বসালে এর মান শূন্য হয়।

অন্যদিকে, লেখস্থিত নয় এমন কোনো বিন্দুর স্থানাঙ্ক সমীকরণটিকে সিদ্ধ করে না অর্থাৎ ঐ বিন্দুর ভুজ ও কোটির জন্য ax+by+c এর মান শূন্য অপেক্ষা বড় বা ছোট হয়। সমতলস্থ কোনো বিন্দু P এর ভুজ ও কোটি দ্বারা ax+by+c রাশির ও কে যথাক্রমে প্রতিস্থাপন করলে রাশিটির যে মান হয়, তাকে P বিন্দুতে রাশিটির মান বলা হয় এবং উক্ত মানকে সাধারণত f(P) দ্বারা নির্দেশ করা হয়। P বিন্দু লেখস্থিত হলে f(P) = 0, P বিন্দু লেখচিত্রের বহিঃস্থ হলে f(P) > 0 অথবা f (P) < 01

 

 

বাস্তবে লেখচিত্রের বহিঃস্থ সকল বিন্দু লেখ দ্বারা দুইটি অর্ধতলে বিভক্ত হয়; একটি অর্ধতলের প্রত্যেক বিন্দু P এর জন্য f(P) > 0; অপর অর্ধতলের প্রত্যেক বিন্দু P এর জন্য f (P) <0। বলা বাহুল্য, লেখের উপর অবস্থিত প্রত্যেক বিন্দু P এর জন্য f (P) = 01

উদাহরণ ৮.

x + y − 3 = 0 সমীকরণটি বিবেচনা করি।

সমীকরণটি থেকে পাওয়া যায়: y = 3 – X

 

x	0	3	1
y	3	0	2

 

 

(x, y) সমতলে ছক কাগজে ছোট বর্গক্ষেত্রের বাহুর দৈর্ঘ্যকে একক ধরে সমীকরণটির লেখচিত্রটি নিম্নরূপ হয় :

 

 

 

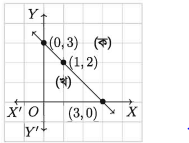
এই লেখচিত্র রেখা সমগ্র তলটিকে তিনটি অংশে পৃথক করে। যথা:

১. রেখার (ক) চিহ্নিত পাশের বিন্দুসমূহ

২. রেখার (খ) চিহ্নিত পাশের বিন্দুসমূহ এবং

৩. রেখাস্থিত বিন্দুসমূহ

এখানে (ক) চিহ্নিত অংশকে লেখরেখার উপরের অংশ ও (খ) চিহ্নিত অংশকে লেখরেখার নিচের অংশ বলা যায় ।

(ক) চিহ্নিত পাশে তিনটি বিন্দু (3, 3), ( 4, 1 ), ( 6, − 1 ) নিই। এই বিন্দুগুলোতে x + y − 3 এর মান যথাক্রমে 3, 2, 2 যাদের সবকটিই ধনাত্মক।

(খ) চিহ্নিত পাশে তিনটি বিন্দু (0, 0 ), (1, 1), (–1, – 1) নিই। এই বিন্দুগুলোতে x + y − 3 এর – মান যথাক্রমে – 3, − 1, 5 যাদের সবকটিই ঋণাত্মক।

 

বিশেষ দ্রষ্টব্য:

ax+by+ c = 0 লেখরেখার এক পাশে একটি বিন্দু নিয়ে সেখানে ax+by+c এর মান নির্ণয় করে রেখাটির দুই পাশ (ধনাত্মক ও ঋণাত্মক) নির্ণয় করা যায়।