সরল সহসমীকরণের সমাধান

আজকে আমাদের আলোচনার বিষয়ঃ সরল সহসমীকরণের সমাধান ।  এটি নবম – দশম শ্রেনী গণিতের দুই চলকবিশিষ্ট সরল সহসমীকরণ এর অন্তর্গত।

 

 

সরল সহসমীকরণের সমাধান

আমরা শুধু সমঞ্জস ও পরস্পর অনির্ভরশীল সরল সহসমীকরণের সমাধান সম্পর্কে আলোচনা করবো। এরূপ সমীকরণজোটের একটিমাত্র (অনন্য) সমাধান আছে।

এখানে, সমাধানের চারটি পদ্ধতির উল্লেখ করা হলো:

১. প্রতিস্থাপন পদ্ধতি ২. অপনয়ন পদ্ধতি ৩. আড়গুণন পদ্ধতি ও ৪. লৈখিক পদ্ধতি।

আমরা অষ্টম শ্রেণিতে প্রতিস্থাপন ও অপনয়ন পদ্ধতিতে সমাধান কীভাবে করতে হয় জেনেছি। এ দুই পদ্ধতির একটি করে উদাহরণ দেওয়া হলো:

উদাহরণ ২.

প্রতিস্থাপন পদ্ধতিতে সমাধান কর :

2x + y = 8

3x – 2y = 5

সমাধান:

প্রদত্ত সমীকরণদ্বয়

2x + y = 8… (1)

3x – 2y = 5…(2)

সমীকরণ (1) হতে পাই, y = 8 – 2x… (3)

সমীকরণ (2) এ y এর মান ৪ – 2x বসিয়ে পাই,

3x – 2 ( 8 – 2x ) = 5

বা, 3x – 16 + 4x = 5

বা, 7x = 5 + 16

বা, 7x = 21

বা, x = 3

x এর মান সমীকরণ (3) এ বসিয়ে পাই,

y=8-2×3

বা, y = 8 – 6

বা, y = 2

সমাধান (x, y) = (3, 2)

 

 

প্রতিস্থাপন পদ্ধতি (Substitution method):

সুবিধামত একটি সমীকরণ থেকে একটি চলকের মান অপর চলকের মাধ্যমে প্রকাশ করে প্রাপ্ত মান অপর সমীকরণে বসালে এক চলকবিশিষ্ট সমীকরণ পাওয়া যায়। অত:পর সমীকরণটি সমাধান করে চলকটির মান পাওয়া যায়। এই মান প্রদত্ত সমীকরণের যে কোনোটিতে বসানো যেতে পারে। তবে যেখানে একটি চলককে অপর চলকের মাধ্যমে প্রকাশ করা হয়েছে সেখানে বসালে সমাধান সহজ হয়। এখান থেকে অপর চলকের মান পাওয়া যায়।

উদাহরণ ৩.

অপনয়ন পদ্ধতিতে সমাধান কর:

2x + y = 8

3x – 2y = 5

দ্রষ্টব্য:

প্রতিস্থাপন ও অপনয়ন পদ্ধতির পার্থক্য বুঝাতেই উদাহরণ ২ এর সমীকরণদ্বয়ই উদাহরণ ৩ এ নেয়া হলো।

সমাধান:

প্রদত্ত সমীকরণদ্বয়

2x + y = 8… (1)

3x-2y=5… (2)

সমীকরণ (1) এর উভয়পক্ষকে 2 দ্বারা গুণ করে, 4x + 2y = 16 (3)

সমীকরণ (2) ও (3) যোগ করে পাই,

7x = 21

বা, x = 3

x এর মান সমীকরণ (1) এ বসিয়ে পাই,

2 x 3 + y = 8

বা, y = 8 – 6

বা, y = 2

সমাধান (x, y) = (3, 2)

 

 

অপনয়ন পদ্ধতি (Elimination method) :

সুবিধামত একটি সমীকরণকে বা উভয় সমীকরণকে এরূপ সংখ্যা দিয়ে গুণ করতে হবে যেন গুণনের পর উভয় সমীকরণের যেকোনো একটি চলকের সহগের পরমমান সমান হয়। এরপর প্রয়োজনমত সমীকরণ দুইটিকে যোগ বা বিয়োগ করলে সহগ সমানকৃত চলকটি অপনীত বা অপসারিত হয়। তারপর সমীকরণটি সমাধান করলে বিদ্যমান চলকটির মান পাওয়া যায়। ঐ মান সুবিধামত প্রদত্ত সমীকরণদ্বয়ের যেকোনোটিতে বসালে অপর চলকটির মান পাওয়া যায়।

আড়গুণন পদ্ধতি (Cross multiplication method):

আড়গুণন পদ্ধতিকে বজ্রগুণন পদ্ধতিও বলে।

নিচের সমীকরণ দুইটি বিবেচনা করি:

a1 + by + c = 0… ( 1 )

a2 + b2y + c2 = 0… ( 2 )

সমীকরণ (1) কে b½ দিয়ে ও সমীকরণ (2) কে b দিয়ে গুণ করে পাই,

a1 b2x + b1b2y + b2c1 = 0… ( 3 )

a2b1x + b1b2y + b1c2 = 0… ( 4 )

সমীকরণ (3) থেকে সমীকরণ (4) বিয়োগ করে পাই,

( a1b2 – a2b1 )x + b2c1 – b1c2 = 0

বা, (a1b2 = a2b1 ) x = b1c2 – b2c1

বা, x/b1c2 – b2c1 = 1/a1b2 – a2b1 ……. (5)

আবার, সমীকরণ (1) কে  a2 দিয়ে ও সমীকরণ (2) কে a1 দিয়ে গুণ করে পাই,

a1a2x + a2b1y + C1a2 = 0… ( 6 )

a1a2x + a1b2y + C2a1 = 0…(7)

সমীকরণ (6) থেকে সমীকরণ ( 7 ) বিয়োগ করে পাই,

(a2b1 – a1b2) y + C1a2 – C2a1 = 0

বা, – (a1b2 = a2b1) y = – (C1a2 – C2a1 )

বা, y/(C1a2 – C2a1 ) = 1/(a1b2 – a2b1) ….(8)

সমীকরণ (5) ও (8) থেকে পাই,

x/b1c2 – b2c1 = y/(C1a2 – C2a1 ) = 1/(a1b2 – a2b1)

x ও y এর এরূপ সম্পর্ক থেকে এদের মান নির্ণয়ের কৌশলকে আড়গুণন পদ্ধতি বলে।

x ও y এর উল্লেখিত সম্পর্ক থেকে পাই,

x/b1c2 – b2c1 = 1/a1b2 – a2b1

বা, b1c2 – b2c1 /a1b2 – a2b1

আবার,

y/(C1a2 – C2a1 ) = 1/(a1b2 – a2b1)

বা, y = (C1a2 – C2a1 )/(a1b2 – a2b1)

প্রদত্ত সমীকরণদ্বয়ের সমাধান: (x, y) = (b1c2 – b2c1 /a1b2 – a2b1 , C1a2 – C2a1 /a1b2 = a2b1)

 

 

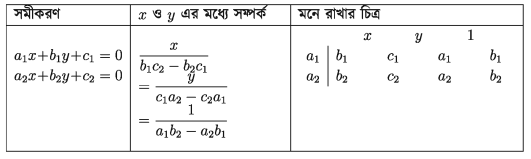
দ্রষ্টব্য:

প্রদত্ত উভয় সমীকরণের ধ্রুবক পদ ডানপক্ষে রেখেও আড়গুণন পদ্ধতি প্রয়োগ করা যায়। তবে সেক্ষেত্রে চিহ্নের কিছু পরিবর্তন হবে। কিন্তু সমাধান একই পাওয়া যাবে।

উদাহরণ ৪.

আড়গুণন পদ্ধতিতে সমাধান কর:

6x – y = 1
3x + 2y = 13

সমাধান:

পক্ষান্তর প্রক্রিয়ায় প্রদত্ত সমীকরণদ্বয়ের ডানপক্ষ 0 (শূন্য) করে পাই,

6x – y – 1 = 0
3x + 2y – 13 = 0

সমীকরণদ্বয়কে যথাক্রমে

a1 x + by + 1 = 0 এবং
a2x + by + c2 = 0

এর সাথে তুলনা করে পাই,

a1 = 6, by = − 1,q = -1
a2 = 3, b2 = 2, 2 = -13

আড়গুণন পদ্ধতিতে পাই,

x/b1c2 – b2c1 = y/(C1a2 – C2a1 ) = 1/(a1b2 – a2b1)

বা, x/(−1) × (−13) − 2 × (−1) = y/(−1) × 3 − (-13) × 6 = 1/ 6 x 2-3 × (-1)

বা, x/(13+2) =  y /(-3+78) =  1/( 12+3)

বা, x/15 =  y /75 =  1/15

সুতরাং,  x/15 =  1/15 বা, x =15/15 = 1 ,

আবার, y /75 =  1/15 বা, y = 75/15 = 3

সমাধান (x, y) = (1, 5 )

 

 

উদাহরণ ৫.

আড়গুণন পদ্ধতিতে সমাধান কর:

3x-4y=0
2x-3y=-1

সমাধান:

প্রদত্ত সমীকরণদ্বয়

3x-4y=0

2x-3y=-1

বা, 3x4y+0=0

2x-3y+1=0

আড়গুণন পদ্ধতিতে পাই,

x/-4 x 1-(-3) × 0 = y / 0×2-1 x 3 =  1 /3 x (-3)-2x (-4)

বা, x/-4 + 0 = y / 0-3 =  1 /-9 + 8

বা, x/-4 = y /-3 =  1 /-1

বা, x/4 = y /3 =  1

সুতরাং, x/4 = 1/1

বা, x = 4

আবার, y/3 = 1/1

বা,  y = 3

সমাধান (x, y) = ( 4, 3 )

উদাহরণ ৬.

আড়গুণন পদ্ধতিতে সমাধান কর:

x/2  +y/3 = 8

5х /4 -3y = -3

সমাধান:

প্রদত্ত সমীকরণদ্বয়কে ax + by + c = 0 আকারে সাজিয়ে পাই,

x/2  +y/3 = 8

বা, 3x+2y/6 = 8

বা, 3x+2y = 48

আবার, 5x/4 -3y=-3

বা, 5x – 12y /4 = -3

বা, 5x -12y+12=0

সমীকরণদ্বয়

3x + 2y – 48 = 0

5x – 12y+12=0

আড়গুণন পদ্ধতিতে পাই,

বা, x/2 x 12 × (-12) × (-48)  = y /(-48) × 5 x (-12) × 3 =  1 /3 x (-12) -5 x 2

বা, x/24-576 = y /-240-36 =  1 /-36-10

বা, x/-552 = y /-276 =  1 /-46

বা, x/552 = y /276 =  1 /46

বা, x/-552  =  1 /-46

x = 552/46 = 12

y /276 =  1 /46

y = 276/46 = 6

সমাধান: (x, y) = (12, 6 )

সমাধানের শুদ্ধি পরীক্ষা:

প্রাপ্ত x ও y এর মান প্রদত্ত সমীকরণে বসিয়ে পাই,

১ম সমীকরণে, বামপক্ষ = x/2+ y/3 = 12/2 + 6/3 = 6 + 2 = 8 = ডানপক্ষ

২য় সমীকরণে, বামপক্ষ 5x/4 -3y = 5 x 12/ 4 -3 x 6 = 15 – 18 = – 3 = ডানপক্ষ।

সমাধান শুদ্ধ হয়েছে।

 

 

উদাহরণ ৭.

আড়গুণন পদ্ধতিতে সমাধান কর: ar – by = ab = bx – ay

সমাধান:

প্রদত্ত সমীকরণদ্বয়,

ax-by= ab
bx-ay = ab

ax-by- ab = 0
bx-ay – ab = 0

আড়গুণন পদ্ধতিতে পাই,

বা, x/(−b) × (−ab) − (−a)(−ab) = y/(−ab) × b − (−ab) × a

= ax (-a)-bx (-b)

বা, x/(ab² + a2b) = y/(-ab2 – a2b) = 1/-a² + b²

বা, x/ab(a – b) = y/- ab(a – b) = 1 /(a + b) (a − b)

সুতরাং, x/ab(a – b) = 1 /(a + b) (a − b)

x = ab(a – b)/(a + b)(a – b) =  ab(a + b)

আবার,y/- ab(a – b) = 1 /(a + b) (a − b)

y = – ab(a – b)/(a + b) (a − b) = -ab/(a + b)

..(x, y) =( ab(a + b), -ab/(a + b) )

 

অনুশীলনী

প্রতিস্থাপন পদ্ধতিতে সমাধান কর (১ – ৩):

১. 7x-3y=31

9x-5y = 41

২. x/2 + y/3 = 1

x/3 + y/2 = 1

৩. x/a + y/b = 2

ax + by =  a²+b²

অপনয়ন পদ্ধতিতে সমাধান কর (৪ – ৬):

8. 7x-3y= 31

9x – 5y = 41

৫. 7x-8y = -9

5x-4y = -3

৬. ax + by = c

a²x + b²y = c²

আড়গুণন পদ্ধতিতে সমাধান কর (৭ – ১৫):

৭. 2x + 3y+5=0

4x + 7y+6=0

৮. 3x-5y+9=0

5x-3y-1=0

৯. x+2y=7

2x-3y=0

১০. 4x+3y=-12

2x = 5

১১. – 7x+8y = 9

5x-4y = -3

১২. 3x – y – 7 = 0

2x+y-3=0

১৩. ax + by = a²+b²

2bx-ay = ab

১৪. y(3+x) = x(6+y)

3(3 + x)=5(y-1)

১৫. (x+2) (y-3)= y(x − 1)

5x – 11y – 8 = 0