আজকে আমাদের আলোচনার বিষয়ঃ ত্রিভুজের সর্বসমতা ও সদৃশতা। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

ত্রিভুজের সর্বসমতা ও সদৃশতা
সপ্তম শ্রেণিতে ত্রিভুজের সর্বসমতা ও সদৃশতা নিয়ে আলোচনা করা হয়েছে। সাধারণভাবে, সর্বসমতা সদৃশতার বিশেষ রূপ। দুইটি চিত্র সর্বসম হলে সেগুলো সদৃশ; তবে চিত্র দুইটি সদৃশ হলে সেগুলো সবসম নাও হতে পারে।
সদৃশকোণী বহুভুজ:
সমান সংখ্যক বাহুবিশিষ্ট দুইটি বহুভুজের একটির কোণগুলো যদি ধারাবাহিকভাবে অপরটির কোণগুলোর সমান হয়, তবে বহুভুজ দুইটিকে সদৃশকোণী (equiangular) বলা হয়।

সদৃশ বহুভুজ
সমান সংখ্যক বাহুবিশিষ্ট দুইটি বহুভুজের একটির শীর্ষবিন্দুগুলোকে যদি ধারাবাহিকভাবে অপরটির শীর্ষবিন্দুগুলোর সঙ্গে এমনভাবে মিল করা যায় যে, বহুভুজ দুইটির (১) অনুরূপ কোণগুলো সমান হয় এবং (২) অনুরূপ বাহুগুলোর অনুপাতগুলো সমান হয়, তবে বহুভুজ দুইটিকে সদৃশ বহুভুজ বলা হয়।
উপরের চিত্রে আমরা লক্ষ করি যে, ABCD আয়ত ও PQRS বর্গ সদৃশকোণী। কারণ, উভয় চিত্রে বাহুর সংখ্যা 4 এবং আয়তের কোণগুলো ধারাবাহিকভাবে বর্গটির কোণগুলোর সমান (সবগুলো কোণ সমকোণ)। কিন্তু চিত্রগুলোর অনুরূপ কোণগুলো সমান হলেও অনুরূপ বাহুগুলোর অনুপাত সমান নয়। ফলে সেগুলো সদৃশও নয়। ত্রিভুজের ক্ষেত্রে অবশ্য এরকম হয় না।
দুইটি ত্রিভুজের শীর্ষ বিন্দুগুলোর কোণ মিলকরণের ফলে সদৃশতার সংজ্ঞায় উল্লেখিত শর্ত দুইটির একটি সত্য হলে অপরটিও সত্য হয় এবং ত্রিভুজ দুইটি সদৃশও হয়। অর্থাৎ, দুইটি সদৃশ ত্রিভুজ সর্বদা সদৃশকোণী এবং দুইটি সদৃশকোণী ত্রিভুজ সর্বদা সদৃশ।
দুইটি ত্রিভুজ সদৃশকোণী হলে এবং এদের কোনো এক জোড়া অনুরূপ বাহু সমান হলে ত্রিভুজদ্বয় সর্বসম হয়। দুইটি সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলোর অনুপাত ধ্রুবক। নিচে এ সংক্তান্ত উপপাদ্যের প্রমাণ দেওয়া হলো।

উপপাদ্য ৩২.
দুইটি ত্রিভুজ সদৃশকোণী হলে এদের অনুরূপ বাহুগুলো সমানুপাতিক।
বিশেষ নির্বচন:
মনে করি, ABC ও DEF ত্রিভুজদ্বয়ের ∠A = ∠D, ∠B = ∠E এবং ∠C = ∠F
প্রমাণ করতে হবে যে, AB/DE = AC/DF = BC/EF
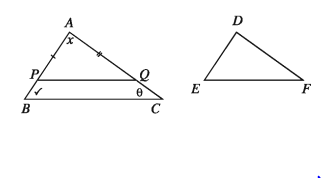
অঙ্কন :
ABC ও DEF ত্রিভুজদ্বয়ের প্রত্যেক অনুরূপ বাহুযুগল অসমান বিবেচনা করি। AB বাহুতে P বিন্দু এবং AC বাহুতে Q বিন্দু নিই যেন AP = DE এবং AQ = DF হয়। P ও Q যোগ করে অঙ্কন সম্পন্ন করি।
প্ৰমাণ:
ধাপ ১.
∆APQ ও ∆DEF এর AP = DE, AQ = DF, ∠A = ∠D
অতএব, ∆APQ ≌ ∆DEF [বাহু-কোণ-বাহুর সর্বসমতা]
সুতরাং, ∠APQ = ∠DEF = ∠ABC এবং ∠AQP = ∠DFE = ∠ACB
অর্থাৎ, PQ রেখাংশ ও BC বাহুকে AB বাহু ও AC রেখা ছেদ করায় অনুরূপ কোণযুগল সমান হয়েছে।
সুতরাং PQ || BC
AB/AP = AC/AQ
AB/DE = AC/DF [অনুসিদ্ধান্ত ১]

ধাপ ২.
একইভাবে BA বাহু ও BC বাহু থেকে যথাক্রমে ED রেখাংশ ও EF রেখাংশের সমান রেখাংশ কেটে নিয়ে দেখানো যায় যে
BA/ED = BC/EF [উপপাদ্য ২৮]
অর্থাৎ AB/DE = BC/EF
AB/DE = AC/DF = BC/EF
উপপাদ্য ৩২ এর বিপরীত প্রতিজ্ঞাটিও সত্য।
উপপাদ্য ৩৩.
দুইটি ত্রিভুজের বাহুগুলো সমানুপাতিক হলে অনুরূপ বাহুর বিপরীত কোণগুলো পরস্পর সমান।
বিশেষ নির্বচন
মনে করি, ∆ABC ও ∆ DEF এর AB/DE = AC/DF = BC/EF।
প্রমাণ করতে হবে যে, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F |

অঙ্কন:
∆ABC ও ∆DEF এর প্রত্যেক অনুরূপ বাহুযুগল অসমান বিবেচনা করি। AB বাহুতে P বিন্দু এবং AC বাহুতে Q বিন্দু নিই যেন AP = DE এবং AQ = DF হয়। P ও Q যোগ করে অঙ্কন সম্পন্ন করি।
প্ৰমাণ:
যেহেতু AB/DE = AC/DF সুতরাং AB/AP = AC/AQ
সুতরাং PQ || BC [উপপাদ্য ২৯]
:. ∠ABC = ∠APQ [AB ছেদক দ্বারা উৎপন্ন অনুরূপ কোণ]
এবং ∠ACB = ∠AQP [AC ছেদক দ্বারা উৎপন্ন অনুরূপ কোণ]
:. ∆ABC ও ∆APQ সদৃশকোণী।
সুতরাং, AB/AP = BC/PQ
বা, AB/DE = BC/PQ [উপপাদ্য ৩২]
কিন্তু AB/DE = BC/EF [কল্পনানুসারে]
BC/EF = BC/ PQ
EF = PQ
সুতরাং ∆APQ ও ∆DEF সর্বসম। [বাহু-বাহু-বাহু উপপাদ্য]
∠PAQ = ∠EDF, ∠APQ = ∠DEF, ∠AQP = ∠DFE
∠APQ = ∠ABC এবং ∠AQP = ∠ACB
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
উপপাদ্য ৩৪.
দুইটি ত্রিভুজের একটির এক কোণ অপরটির এক কোণের সমান হলে এবং সমান সমান কোণ সংলগ্ন বাহুগুলো সমানুপাতিক হলে ত্রিভুজদ্বয় সদৃশ।
বিশেষ নির্বচন
মনে করি ∆ABC ও ∆DEF এমন যে, ∠A = ∠D এবং AB/DE = AC/DF
প্রমাণ করতে হবে যে, ∆ABC ও ∆DEF সদৃশ।

অঙ্কন:
∆ABC ও ∆DEF এর প্রত্যেক অনুরূপ বাহুযুগল অসমান বিবেচনা করি। AB বাহুতে P বিন্দু এবং AC বাহুতে Q বিন্দু নিই যেন AP = DE এবং AQ = DF হয়। P ও Q যোগ করে অঙ্কন সম্পন্ন করি।
প্ৰমাণ :
∆APQ ও ∆DEF এর AP = DE, AQ = DF এবং অন্তর্ভুক্ত ∠A = অন্তর্ভুক্ত ∠D
∆APQ ≌ ∆DEF [বাহু-কোণ-বাহু উপপাদ্য]
∠A = ∠D, ∠APQ = ∠E, ∠AQP = ∠F
আবার যেহেতু AB/DE = AC/DF
সুতরাং AB/AP = AC/ AQ [উপপাদ্য ২৯]
PQ || BC
সুতরাং ∠ABC = ∠APQ এবং ∠ACB = ∠AQP
∠A = ∠D, ∠B = ∠E, এবং ∠C = ∠F
অর্থাৎ ∆ABC ও ∆DEF সদৃশকোণী।
সুতরাং ∆ABC ও ∆DEF সদৃশ।
উপপাদ্য ৩৫.
দুইটি সদৃশ ত্রিভুজক্ষেত্রের ক্ষেত্রফলদ্বয়ের অনুপাত এদের যেকোনো দুই অনুরূপ বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলদ্বয়ের অনুপাতের সমান।
বিশেষ নির্বচন:
মনে করি, ∆ABC ও ∆DEF ত্রিভুজদ্বয় সদৃশ এবং এদের অনুরূপ বাহু BC ও EF।
প্রমান করতে হবে যে, ∆ABC : ∆DEF = BC2 : EF2

অঙ্কন:
BC ও EF এর উপর যথাক্রমে AG ও DH লম্ব আঁকি। মনে করি AG = h, DH = p
প্ৰমাণ:
ধাপ ১.
∆ABC = 1/2 × BC × h এবং ΔDEF = 1/2 × EF × p
∆ABC/ΔDEF = (1/2 × BC × h) /(1/2 × EF × p ) = h/p × BC /EF
ধাপ ২.
ABG DEH ত্রিভুজদ্বয় ∠B = ∠E, ∠AGB = ∠DHE [এক সমকোণ]
∠BAG = ∠EDH
∆ABC ও ∆DEF ত্রিভুজদ্বয় সদৃশকোণী, তাই সদৃশ।
h/Р = AB/DE = BC/EF [কারণ ∆ABC ও ∆DEF সদৃশ]
ধাপ ৩.
∆ABC/∆DEF = h/Р × BC/EF = BC/EF × BC/EF = BC2/EF2
