সসীম ধারা

আজকে আমাদের আলোচনার বিষয়ঃ সসীম ধারা।  এটি নবম – দশম শ্রেনী গণিতের সসীম ধারার অন্তর্গত।

 

 

সসীম ধারা

প্রাত্যহিক জীবনে ‘ক্রম’ বহুল প্রচলিত একটি শব্দ। যেমন – দোকানের তাকে ভোগ্যপণ্য সাজাতে, নাটক ও অনুষ্ঠানের ঘটনাবলী সাজাতে, গুদামঘরে সুন্দরভাবে দ্রব্যাদি রাখতে ক্রমের ধারণা ব্যবহৃত হয়। আবার অনেক কাজ সহজে এবং দৃষ্টিনন্দনভাবে সম্পাদন করতে আমরা বড় হতে ছোট, শিশু হতে বৃদ্ধ, হালকা হতে ভারী ইত্যাদি বিভিন্ন ধরনের ক্রম ব্যবহার করি। এই ক্রমের ধারণা হতেই বিভিন্ন প্রকার গাণিতিক ধারার উদ্ভব হয়েছে। এই অধ্যায়ে অনুক্রম ও ধারার মধ্যে সম্পর্ক ও এতদ সংক্রান্ত বিষয়বস্তু উপস্থাপন করা হয়েছে।

অনুক্রম (Sequence )

নিচের সম্পর্কটি লক্ষ করি :

 

 

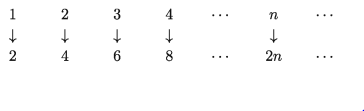
এখানে প্রত্যেক স্বাভাবিক সংখ্যা n তার দ্বিগুণ সংখ্যা 2n এর সাথে সম্পর্কিত। অর্থাৎ স্বাভাবিক সংখ্যার সেট {1,2,3,··· } থেকে একটি নিয়মের মাধ্যমে যোগবোধক জোড় সংখার সেট {2, 4, 6, … } পাওয়া যায়। এই সাজানো জোড়সংখ্যার সেটটি একটি অনুক্রম। সুতরাং, কতকগুলো রাশি একটা বিশেষ নিয়মে ক্রমান্বয়ে এমনভাবে সাজানো হয় যে প্রত্যেক রাশি তার পূর্বের পদ ও পরের পদের সাথে কীভাবে সম্পর্কিত তা জানা যায়। এভাবে সাজানো রাশিগুলোর সেটকে অনুক্রম (Sequence) বলা হয়।

 

 

উপরের সম্পর্কটিকে ফাংশন বলে এবং f(n) = 2n লিখা হয়। এই অনুক্রমের সাধারণ পদ 2n যেকোনো অনুক্রমের পদসংখ্যা অসীম। অনুক্রমটি সাধারণ পদের সাহায্যে লিখার পদ্ধতি হলো {2n}, n = = 1,2,3,··· বা, {2n}n=1 বা, {2n}।

অনুক্রমের প্রথম রাশিকে প্রথম পদ, দ্বিতীয় রাশিকে দ্বিতীয় পদ, তৃতীয় রাশিকে তৃতীয় পদ ইত্যাদি বলা হয়। 1, 3, 5, 7, … অনুক্রমের প্রথম পদ 1, দ্বিতীয় পদ 3, ইত্যাদি। নিচে অনুক্রমের চারটি উদাহরণ দেওয়া হলো:

 

 

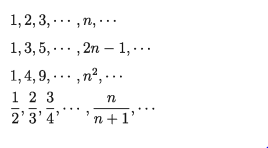
ধারা (Series)

কোনো অনুক্রমের পদগুলো পরপর + চিহ্ন দ্বারা যুক্ত করলে একটি ধারা (Series) পাওয়া যায়। যেমন, 1 + 3 + 5 + 7 + … একটি ধারা। ধারাটির পরপর দুইটি পদের পার্থক্য সমান। আবার 2+4+8+16+… একটি ধারা। এর পরপর দুইটি পদের অনুপাত সমান। সুতরাং, যেকোনো ধারার পরপর দুইটি পদের মধ্যে সম্পর্কের উপর নির্ভর করে ধারাটির বৈশিষ্ট্য। ধারাগুলোর মধ্যে গুরুত্বপূর্ণ দুইটি ধারা হলো সমান্তর ধারা ও গুণোত্তর ধারা ।