আমাদের আজকের আলোচনার বিষয় সাংখ্যিক সহগ – যা অজানা রাশির জগৎ অধ্যায় এর অন্তর্ভুক্ত।১৭শ শতক পর্যন্ত কেবল পাটীগণিত, বীজগণিত ও জ্যামিতিকে গাণিতিক শাস্ত্র হিসেবে গণ্য করা হত। সেসময় গণিত দর্শন ও বিজ্ঞানের চেয়ে কোন পৃথক শাস্ত্র ছিল না। আধুনিক যুগে এসে গণিত বলতে যা বোঝায়, তার গোড়াপত্তন করেন প্রাচীন গ্রিকেরা, পরে মুসলমান পণ্ডিতেরা এগুলি সংরক্ষণ করেন, অনেক গবেষণা করেন এবং খ্রিস্টান পুরোহিতেরা মধ্যযুগে এগুলি ধরে রাখেন। তবে এর সমান্তরালে ভারতে এবং চীন-জাপানেও প্রাচীন যুগ ও মধ্যযুগে স্বতন্ত্রভাবে উচ্চমানের গণিতচর্চা করা হত। ভারতীয় গণিত প্রাথমিক ইসলামী গণিতের উপর গভীর প্রভাব ফেলেছিল।
১৭শ শতকে এসে আইজাক নিউটন ও গটফ্রিড লাইবনিৎসের ক্যালকুলাস উদ্ভাবন এবং ১৮শ শতকে অগুস্তঁ লুই কোশি ও তার সমসাময়িক গণিতবিদদের উদ্ভাবিত কঠোর গাণিতিক বিশ্লেষণ পদ্ধতিগুলির উদ্ভাবন গণিতকে একটি একক, স্বকীয় শাস্ত্রে পরিণত করে। তবে ১৯শ শতক পর্যন্ত কেবল পদার্থবিজ্ঞানী, রসায়নবিদ ও প্রকৌশলীরাই গণিত ব্যবহার করতেন।

সাংখ্যিক সহগ
আমরা জানতে পারলাম পদগুলো কীভাবে দুই বা ততোধিক উৎপাদকের গুলফলের মাধ্যমে লেখা যায়। আমরা আরও বুঝতে পারলাম পদের উৎপাদকগুলোর মধ্যে কোনোটি সংখ্যা আবার কোনোটি বীজগণিতীয় রাশি বা প্রতীক। কোনো পদের চলকের সাথে যখন সংখ্যা গুণক হিসেবে যুক্ত থাকে, তখন ঐ গুণককে সাংখ্যিক সহগ বা সহগ বলব।
যেমন: 4x, 6xy,-15xyz এর সাংখ্যিক সহগ যথাক্রমে 4, 6, -15
বীজগণিতীয় রাশির কোনো পদের সাথে যখন কোনো সংখ্যা গুণক হিসেবে যুক্ত থাকে না, তখন ঐ রাশি বা পদের সহগ 1 ধরা হয়। কারণ 1.x কে লেখা হয় শুধুমাত্র x, 1xy কে লেখা হয় শুধুমাত্র xy ইত্যাদি। সুতরাং x, এবং -xy এর সহগ যথাক্রমে 1 এবং -1 আর যখন কোনো চলকের সাথে কোনো অক্ষর প্রতীক’ গুণক হিসেবে যুক্ত থাকে, তখন ঐ গুণককে রাশি বা পদের আক্ষরিক সহগ বলে থাকি।
মনে করো 10abc একটি একপদী রাশি। এখানে 10 হলো abc এর সাংখ্যিক সহগ, a হলো 10bc এর, b হলো 10ac এর এবং c হলো 10ab এর আক্ষরিক সহগ।
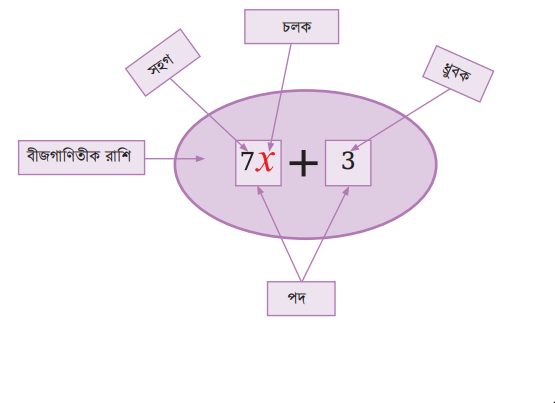
তাহলে একটি বীজগাণিতিক রাশিকে কাটাকুটি করলে কী কী পাওয়া যায়, তা একনজরে দেখে নিই