আজকে আমাদের আলোচনার বিষয়ঃ একাধিক সাধারণ ভগ্নাংশের সাধারণ গুণনীয়ক ও গসাগু । এটি সপ্তম শ্রেনী গণিতের ভগ্নাংশের গসাগু ও লসাগু এর অন্তর্গত।

একাধিক সাধারণ ভগ্নাংশের সাধারণ গুণনীয়ক ও গসাগু
এপর্যন্ত আমরা সাধারণ ভগ্নাংশের গুণনীয়ক সম্বন্ধে জেনেছি। আমরা এখন, একাধিক সাধারণ ভগ্নাংশের জন্য সাধারণ গুণনীয়ককের ধারণাটি বোঝার চেষ্টা করব। এক্ষেত্রে মূল ধারণাটি কিন্তু আমাদের পূর্ণ সংখ্যার যে সাধারণ গুণনীয়ককের ধারণা, সেটিই। অর্থাৎ, সাধারণ গুণনীয়ক নির্ণয় করতে হবে, একাধিক সাধারণ ভগ্নাংশের গুণনীয়কের তুলনার মাধ্যমে।
এক্ষেত্রে চলো একটি উদাহরণের সাহায্যে বিষয়টি বোঝা যাক। দুটি ভগ্নাংশ ১/৬ ও ১/৮নিই।
এখন এই দুটি ভগ্নাংশের ১০ টি করে সাধারণ গুণনীয়ক নির্ণয় করব আমরা। সেটি নিচের ছকে লেখা হয়েছে।
ছক ১
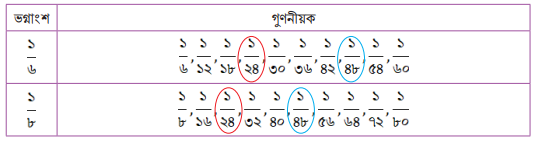
উপরের ছকে চিহ্নিত করো তো কোন ভগ্নাংশ দুটি উভয় সারিতেই রয়েছে? খুব সহজেই দেখতে পারবে ১/২৪ এবং ১/৪৮ ছকের উভয় সারিতেই রয়েছে। তাহলে পূর্ণসংখ্যার সাধারণ গুণনীয়ককের ধারণা থেকে এক্ষেত্রেও বলা সম্ভব যে ১/২৪ এবং ১/৪৮ হলো ১/৬ ও ১/৮ এর সাধারণ গুণনীয়ক।
এখন আমরা আবার পূর্বের উদাহরণে চলে যাই। সেখান থেকে আমরা সাধারণ গুণনীয়কগুলো পেয়েছি ১/২৪ ও ১/৪৮ । এবার বলো তো এদের মধ্যে কোনটি বড়?
তোমরা কিন্তু সমহরবিশিষ্ট ভগ্নাংশ তৈরি করা শিখেছো। উদাহরণ হিসেবে আমরা চাইলে ১/২ ও ১/৩ ভগ্নাংশ দুটি দেখতে পারি। এদেরকে সমহর বিশিষ্ট ভগ্নাংশ করতে হলে কী করতে হবে? প্রথমেই সমহর কথাটি যখন আসছে, বোঝাই যাচ্ছে, দুটি ভগ্নাংশের হরকে সমান করতে হবে। এক্ষেত্রে কি হবে? দুটি ভগ্নাংশেরই হর হবে ৬। কেননা ২ ও ৩ এর লসাগু হয় ৬। এখন ভগ্নাংশ দুটির লবের কথাও তো চিন্তা করতে হবে। নতুন সমহর ভগ্নাংশের লব কি হবে? এক্ষেত্রে আমরা আবার গ্রিডের সাহায্য নিয়ে ভাবতে পারি।

গ্রিড থেকে কী দেখা যাচ্ছে? হর ৬ হলে, এর লব হবে ৩। কারণটি কিন্তু খুব সহজ। গ্রিড থেকে পাই, হর ৬ হতে হলে, মূল কাঠামোটিকে পূর্বের ২ ভাগের জায়গায় ৬ ভাগ করা হচ্ছে। এতে বেগুনি রঙের ঘরের সংখ্যা ভাগ ১ থেকে বেড়ে হয় ৩। অর্থাৎ, মোট ঘরসংখ্যা ৬ হলে, বেগুনি রঙের ঘরের সংখ্যা ৩ হচ্ছে। তার মানে হর যে গুণিতকে বাড়ছে, লবও সেই গুণিতকে বাড়বে। তাহলে, লব হবে (১×৩) = ৩। তাহলে নতুন ভগ্নাংশটি হচ্ছে ৩/৬। তেমনিভাবে ১/৩ এই ভগ্নাংশটির হর এখন ৬। সেক্ষেত্রে নতুন ভগ্নাংশটি হবে ২/৬। এখান থেকে খুব সহজেই বোঝা যাচ্ছে ৩/৬ > ২/৬ । এর মানে হল, ১/২ > ১/৩।
এবার চিন্তা করে দেখো তো, ১/২৪ ও ১/৪৮ এর মাঝে কোনটি বড়?
এখানে ভগ্নাংশ দুটির হরের লসাগু ৪৮। তাহলে সমহরের ধারণা থেকে সহজেই নির্ণয় করা যায়, ১/২৪ = ১/৪৮ ।
অর্থাৎ, ২/৪৮ > ১/৪৮
তার মানে বড় ১/২৪ । তাহলে এই ১/২৪ ই হল ভগ্নাংশ দুটির জন্য গরিষ্ঠ সাধারণ গুণনীয় বা গসাগু = ৪৮
এখন তোমরা চিন্তা করো আমরা এতক্ষণ এমন দুটি ভগ্নাংশ নিয়ে কাজ করেছি, যাদের লব শুধুমাত্র ১। এবার একটু ভিন্ন কিছু নিয়ে ভাবা যাক। এবার চলো আমরা ভগ্নাংশ হিসেবে- ও – নিই। এদের গসাগু নির্ণয় করতে হবে। 8 তাহলে চলো প্রথমেই গসাগু নির্ণয়ের নিয়ম অনুযায়ী এদের গুণনীয়কগুলো খুঁজে বের করার চেষ্টা করি। প্রথমেই – এর গুণনীয়কগুলো কি হবে? আমরা কিন্তু জানি সবগুলো গুণনীয়ক খুঁজে বের করা সম্ভব নয়। 8 তাহলে ১০ টি গুণনীয়ক বের করার চেষ্টা করি।
ছক ২

এখন ভাবো তো ২/৫ এর গুণনীয়কগুলো কি হবে? চলো খুঁজে দেখার চেষ্টা করি।
ছক ৩
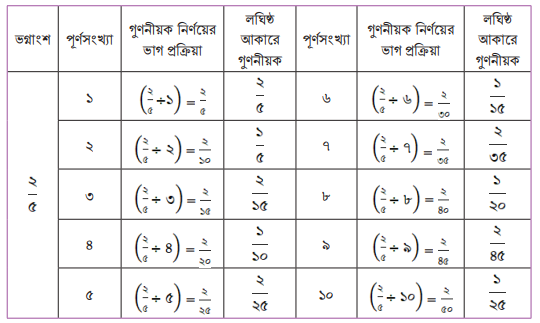
এখান থেকে দেখো, ১০ টি করে গুণনীয়ক নির্ণয়ের পর খুব সহজেই আমরা দেখতে পাচ্ছি দুটি ভগ্নাংশের মাত্র একটি সাধারণ গুণনীয়ক পাওয়া যাচ্ছে। সেটি হলো ১/১০। প্রশ্ন হলো আমরা এটিকেই গসাগু বলতে পারব কিনা ? কারণ সাধারণ ভগ্নাংশের ক্ষেত্রে কিন্তু পূর্ণসংখ্যার মত করে নির্দিষ্ট সংখ্যক গুণনীয়ক থাকে না। এর মানে হলো, সাধারণ গুণনীয়কের সংখ্যাও কিন্তু আসলে নির্দিষ্ট নয়। অর্থাৎ, একাধিক সাধারণ দশমিক ভগ্নাংশের সাধারণ গুণনীয়কগুলোর সংখ্যাও অসীম।
এবার তাহলে তোমার এপর্যন্ত করা কাজের মাধ্যমে সাধারণ গুণনীয়কগুলোর মাঝে কি কোন সম্পর্ক পাওয়া যায়? আমরা যদি পূর্বে আমাদের দেখানো উদাহরণ ১/৬ ও ১/৮ এর কথা ভাবি, তাহলে দেখতে পারবো যে, ভগ্নাংশ দুটির সাধারণ গুণনীয়ক ছিল ১/২৪ ও ১/৪৮ । এবার চলো আমরা এই বিষয়ে আরেকটু কাজ করি। আমরা ৪৮ এবার এই ভগ্নাংশ দুটির ১২ টি করে গুণনীয়ক নির্ণয় করব।
ছক ৪

এখান থেকে কি দেখা যাচ্ছে? আমরা কি নতুন কোন সাধারণ গুণনীয়ক পেয়েছি? চিহ্নিত অংশ থেকে দেখতে পাবে, ১/৭২ ও এই ভগ্নাংশ দুটির সাধারণ গুণনীয়ক।
এখন একটি বিষয় চিন্তা করো। আমরা কিন্তু সাধারণ গুণনীয়কগুলোর মাঝেও চাইলে একটি সম্পর্ক নির্ণয় করতে পারব। নিচে দেখো,
অর্থাৎ, ক্রমানুযায়ী গুণনীয়ক নির্ণয় করে প্রাপ্ত প্রথম সাধারণ গুণনীয়কটির সাহায্যে চাইলে অন্য সাধারণ গুণনীয়কগুলো পাওয়া সম্ভব। যেভাবে আমরা ভাগ করে করে ভগ্নাংশের সাধারণ গুণনীয়ক নির্ণয় করেছি সেভাবেই প্রথম প্রাপ্ত সাধারণ গুণনীয়কটিকে ক্রমানুযায়ী পূর্ণসংখ্যাগুলো দ্বারা ভাগ করে গেলেই সাধারণ গুণনীয়কগুলো নির্ণয় করা যাবে।
এখন চিন্তা করো, তুমি যখন কাগজ ভাঁজ করেছিলে, ভাঁজ করে পাওয়া ভাগগুলো বড় ছিল নাকি কাগজটি বড় ছিল? অবশ্যই কাগজটি বড় ছিল, কারণ সেই একটি কাগজের মাঝেই বারবার ভাগ করা হচ্ছিল। এখান থেকে কিন্তু সহজেই ধারণা করা যায়, একটি ভগ্নাংশকে আরেকটি পূর্ণসংখ্যা দ্বারা ভাগ করা হলে নতুন পাওয়া ভাগফল বা ভগ্নাংশটি অবশ্যই মূল ভগ্নাংশের তুলনায় ছোট হবে।
এখন তাহলে এখান থেকে কি বুঝলে বলো তো? ক্রমানুযায়ী যদি সাধারণ গুণনীয়ক নির্ণয় করা হয়, তাহলে একদম প্রথমে যে সাধারণ গুণনীয়কটি পাওয়া যাবে, সেটিই হবে সবচেয়ে বড় সাধারণ গুণনীয়ক বা গসাগু
এখন তাহলে কি বলা যায় বলো তো? আমরা ১০ টি করে গুণনীয়ক নির্ণয় করে- ও -এর যে একমাত্র সাধারণ 8 গুণনীয়কটি পেয়েছি, সেই.১/২০ই হল ভগ্নাংশ দুটির গসাগু।
এবার চিন্তা করো তো, ১/৪ ও ৩/১১ এর গসাগু নির্ণয় করতে পারব কীনা? তাহলে চলো ১০ টি করে গুণনীয়ক নিয়ে গসাগু নির্ণয় করার চেষ্টা করি।
ছক ৫
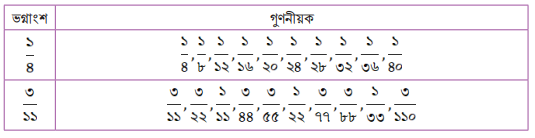
এখন বলো তো এই ভগ্নাংশ দুটির সাধারণ গুণনীয়ক কত? ছক থেকে কিন্তু কোন সাধারণ গুণনীয়ক পাওয়া যাচ্ছে না। কিন্তু ভগ্নাংশ দুটির অবশ্যই একটি সাধারণ গুণনীয়ক রয়েছে। এবার তাহলে চলো আমরা মোট ১৫ টি করে সাধারণ গুণনীয়ক নির্ণয় করার চেষ্টা করি।
ছক ৬
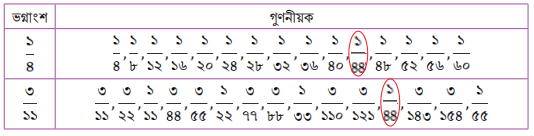
এবার দেখো, আমরা কিন্তু একটি সাধারণ গুণনীয়ক পেয়েছি, সেটি হল ১/৪৪। এখন কিন্তু আমরা বলতে পারব যে এই ১/৪৪ ই ভগ্নাংশ দুটির নির্ণেয় গসাগু।
একটি বিষয় চিন্তা করো, ধনাত্মক পূর্ণসংখ্যার ক্ষেত্রে গুণনীয়ককের সংখ্যা নির্দিষ্ট ছিল। তাই চাইলেই এভাবে গুণনীয়ক নির্ণয় করে আমরা সাধারণ গুণনীয়ক কিংবা গসাগু নির্ণয় করতে পেরেছি। কিন্তু ভগ্নাংশের ক্ষেত্রে বিষয়টি নির্দিষ্ট নয়। একারণে আমরা চাইলে বুঝতে পারব না যে ঠিক কতটি করে গুণনীয়ক নেয়া প্রয়োজন। যেমন ১/৬ ও ১/৮ এর ক্ষেত্রে ৪ টি করে গুণনীয়ক বের করলেই কিন্তু আমরা গসাগুটি পেতে পারতাম।
আবার ১/8 ও ২/৫ এর ক্ষেত্রে আমাদের ন্যুনতম ৮ টি গুণনীয়ক নির্ণয় করা প্রয়োজন ছিল গসাগু নির্ণয় করার জন্য। আবার পরবর্তীতে ১/৪ ও ৩/১১ এর ক্ষেত্রে কিন্তু আমরা দেখতে পাচ্ছি আমাদের ১০ টি গুণনীয়ক নির্ণয় করলেই হয় না। অন্তত ১২ টি গুণনীয়ক নির্ণয় করতে পারলে গসাগুটি পাওয়া যাবে। এটি কিন্তু অনেক সময় সাপেক্ষ এবং প্রতিটি ভগ্নাংশের জন্য ন্যুনতম কতটি গুণনীয়ক নির্ণয় করলে প্রথম সাধারণ গুণনীয়ক বা গসাগুটি পাওয়া যাবে, সেই সংখ্যাটি অনির্দিষ্ট।
তাহলে এবার চলো তো চিন্তা করা যাক এই সমস্যার কোন সমাধান করা যায় কিনা?
এখানে চিন্তা করে দেখো, আমরা সমহরের ধারণাটি এখানে কোনভাবে প্রয়োগ করতে পারি কিনা?
দেখো, ১/৪ ও ৩/১১ কে কিন্তু চাইলেই সমহর বিশিষ্ট ভগ্নাংশে রুপান্তর করা যায়।
৪ ও ১১ এর লসাগু হল ৪৪। তারমানে সমহরে রুপান্তর করা হলে, পাওয়া যাবে, ১/৪ = ১১/৪৪। কারণ হরে ৪ এর সাথে ১১ গুণ করা হলে ৪৪ পাওয়া যায়। তাহলে লবেও ১১ গুণ করতে হবে সমতার জন্য।
তেমনিভাবে ১২ 88 = 88
এখন চিন্তা করে দেখো, আমাদের দুটি ভগ্নাংশের জন্য হর কিন্তু একই। তাহলে আমাদের কিন্তু হর নিয়ে আর কিছু ভাবতে হচ্ছে না। এখন ভাবো আমরা যদি দুটি ভগ্নাংশকেই ৪৪ দিয়ে গুণ করতাম, তাহলে দুটি পূর্ণ সংখ্যা পেতাম, সেগুলো হল, ১১ ও ১২। এখন বলো তো ১১ ও ১২ এর গসাগু কত? তোমরা কিন্তু ধনাত্মক পূর্ণসংখ্যার গসাগু কীভাবে নির্ণয় করতে হয় তা জানো। আমরা বলতে পারি ১১ ও ১২ এর গসাগু কিন্তু ১ হবে।
আবার সমতা করার জন্য ১১ ও ১২ এর গসাগুকে কিন্তু ৪৪ দিয়ে ভাগ করা প্রয়োজন। কারণ আমাদের প্রাপ্ত ভগ্নাংশ দুটি ছিল ১১/৪৪ ও ১২/৪৪ । অর্থাৎ, গসাগু হবে ১/88।
এখান থেকে তাহলে কি বোঝা যায়? একাধিক সাধারণ ভগ্নাংশের যদি হর একই হয়, অর্থাৎ ভগ্নাংশগুলো সমহরবিশিষ্ট হয়, তাহলে, ভগ্নাংশগুলোর গসাগুও একটি ভগ্নাংশ হবে, যে ভগ্নাংশের হরটি সমহর বিশিষ্ট ভগ্নাংশগুলোর হর হবে এবং লবটি সমহরবিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু হবে।
সমহর বিশিষ্ট ভগ্নাংশ দুটির লবের মধ্যে কোনটি বড়? অবশ্যই ১১ ও ১২ এর মাঝে কিন্তু ১২ বড়। এখন চিন্তা করো তো এই দুটি ভগ্নাংশের জন্য আমাদের গসাগু পাওয়ার জন্য ন্যুনতম কতটি করে গুণনীয়ক নির্ণয় করতে হয়েছিল?
এখন তাহলে চলো আমরা দেখি আরও কিছু গসাগু নির্ণয় করতে পারি কিনা ধরো আমাদের ভগ্নাংশ দুটি হল ৩/৫ ও ৬/১৩।
আবার চলো আমরা ভগ্নাংশ দুটিকে সমহর বিশিষ্ট ভগ্নাংশে রুপান্তর করার চেষ্টা করি। ভগ্নাংশ দুটির হর ৫ ও ১৩ এর গসাগু ৬৫। তাহলে সমহরে রুপান্তরিত ভগ্নাংশ দুটি হবে,

এবারকী করতে হবে? হরকে ঠিক রেখে, লবে ৩০ ও ৩৯ এর গসাগু নির্ণয় করতে হবে। ৩০ ও ৩৯ এর গসাগু হল ৩।
অর্থাৎ, ভগ্নাংশ দুটির নির্ণেয় গসাগুটি হবে ৩/৬৫।
এখন এই সমহরবিশিষ্ট ভগ্নাংশ দুটির লবের গসাগু কিন্তু ৩। তার মানে যদি ভগ্নাংশ দুটিকে ৩ দিয়ে ভাগ ১৩ করতাম, তাহলে যে দুটি ভগ্নাংশ পেতাম সেটি কত হত? ১০/৬৫ এবং ১৩/৬৫। এদের লবগুলোর মধ্যে কোনটি বৃহত্তম? তুমি পূর্বে গুণনীয়ককের সাহয্যে যেভাবে গসাগু নির্ণয় করে এসেছিলে সেখানে সাধারণ গুণনীয়ক বা গসাগুটি পাওয়ার জন্য ন্যূনতম কতটি গুণনীয়ক নির্ণয় করার প্রয়োজন হয়েছিল?
তুমি চাইলে এভাবে ধাপে ধাপে কিন্তু কাজটি করতে পারো। নিচে পূর্বে নির্ণয় করে আসা দুটি ভগ্নাংশের গসাগু নির্ণয়ের ধাপ দেখানো হল।
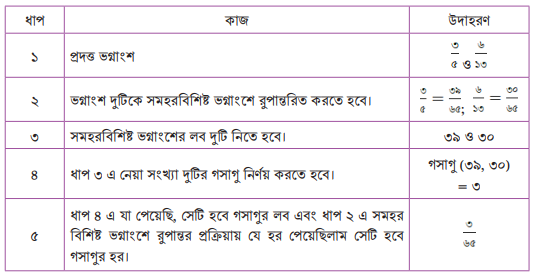
এখন একটি বিষয় ভাবো। আমরা কিন্তু পুরো প্রক্রিয়ায় উদাহরণ হিসেবে ২ টি করে ভগ্নাংশ নিয়ে কাজ করেছি। কিন্তু তুমি চাইলে পূর্বে দেখানো সকল প্রক্রিয়ার মাধ্যমে দুই এর অধিক ভগ্নাংশেরও গসাগু নির্ণয় করতে পারবে।
আমরা কিন্তু ধনাত্মক পূর্ণসংখ্যার গুণিতক কী সেটি জানি। ধনাত্মক পূর্ণসংখ্যার গুণিতক কোনগুলো বলো তো? একদম সহজে বলা যায়, কোন নির্দিষ্ট ধনাত্মক পূর্ণসংখ্যার সাথে আরেকটি ধনাত্মক পূর্ণসংখ্যা গুণ করলে গুণফল পাওয়া যায়, সেটিই ওই নির্দিষ্ট ধনাত্মক পূর্ণসংখ্যার গুণিতক। যেমন ৩ এর গুণিতকগুলো কি হতে পারে? ৩, ৬, ৯, ১২, এভাবে অসীমসংখ্যক। কারণ আমরা জানি পূর্ণসংখ্যা অসীমসংখ্যক। তাহলে উদাহরণ অনুযায়ী ৩ এর সাথে গুণ করার জন্য অসীমসংখ্যক পূর্ণসংখ্যা পাওয়া সম্ভব। তাই যেকোনো ধনাত্মক পূর্ণসংখ্যার গুণিতকও অসীমসংখ্যাক থাকতে পারে।
লসাগুর সাথে গুণিতকের সম্পর্ক রয়েছে। লসাগুর পূর্ণরূপ হলো লঘিষ্ঠ সাধারণ গুণিতক। অর্থাৎ এক্ষেত্রেও একাধিক সংখ্যার প্রয়োজন লসাগু নির্ণয় করতে হলে। আমরা একাধিক সংখ্যার গুণিতক নির্ণয় করলে দেখা যায়, এক বা একাধিক সংখ্যা রয়েছে যা উক্ত সকল সংখ্যারই গুণিতক। সেই একটি বা একাধিক গুণিতককে বলা হয় সাধারণ গুণিতক। এদের মধ্যে যে গুণিতকটি সবচেয়ে ক্ষুদ্র অর্থাৎ, লঘিষ্ঠ সেই গুণিতকটিই হল লঘিষ্ঠ সাধারণ গুণিতক। ভেবে বলো তো একটি মাত্র সাধারণ গুণিতক থাকলে কি হয়?
ধনাত্মক পূর্ণসংখ্যার পাশাপাশি, সাধারণ ভগ্নাংশের ক্ষেত্রেও এই পদ্ধতিতে লসাগু নির্ণয় করা সম্ভব।
