আজকে আমাদের আলোচনার বিষয়ঃ সাধারণ ভগ্নাংশের গুণিতক । এটি সপ্তম শ্রেনী গণিতের ভগ্নাংশের গসাগু ও লসাগু এর অন্তর্গত।

সাধারণ ভগ্নাংশের গুণিতক
তোমরা সাধারণ ভগ্নাংশের গুণনীয়ক সম্পর্ক জেনেছো। এবার চলো আমরা সাধারণ ভগ্নাংশের গুণিতক সম্পর্কে জানার চেষ্টা করব। এবারও তাহলে চলো আমরা একটি খেলা খেলি। এখানেও আমরা গুণনীয়ক নির্ণয়ের খেলার মত খেলা খেলব। তবে এবার উল্টোভাবে।
গুণিতক খুঁজি
তোমরা কয়েকটি দলে ভাগ হয়ে যাও। এবার আগের মতই একটি কাগজকে সমান দুই ভাগে কাটো। এভাবে কাগজটি দুটি খণ্ড হলো এবং প্রতিটি খন্ডই কিন্তু মূল কাগজটির – অংশ। তুমি এরকম কতটি খন্ড পেলে যেটি মূল কাগজের ১/২ অংশ? ২ টি। এবার আরও কিছু কাগজ কেটে এরকম ২০ টি খণ্ড তৈরি করো। প্রতিটি খন্ডের উপরে ১/২ লিখে চিহ্নিত করো।
একইভাবে গুণনীয়কের খেলায় তুমি যেভাবে আরও ৩ টি কাগজ নিয়ে, সেই কাগজগুলোকে যথাক্রমে সমান ৩, ৪ ও ৫ খণ্ডে বিভক্ত করেছিলে এবারও তাই করো।
তুমি যদি ছক ১.১ সম্পূর্ণ করে আসো, তাহলে দেখতে পাবে সমান ৩ খণ্ডে বিভক্ত করলে প্রতিটি খণ্ড হবে ১/৩। এভাবে বাকিগুলোও নির্ণয় করা যাবে। এখন তুমি আরও কাগজ কেটে, े এর মোট ২০ টি খন্ড তৈরি করো। এটিরও প্রতি খন্ডের উপর ১/৩ লিখে চিহ্নিত করো।
একইভাবে বাকি দুটি ভিন্ন আকারের খণ্ডের জন্যেও ২০ টি করে খণ্ড তৈরি করো এবং উপরের নিয়মে চিহ্নিত করো।
এবার প্রথমেই তোমরা – আকারের খণ্ডগুলো নাও। খণ্ডগুলোকে ক্রমান্বয়ে পাশাপাশি সাজাবে।
বসানোর মানে হলো প্রতিবারে গুণ করে যাওয়া। তাহলে এভাবে ক্রমান্বয়ে মোট ২০ টি খন্ড বসাও এবং এর প্রেক্ষিতে নিচের ছক পূরণ করো।

ছক ১
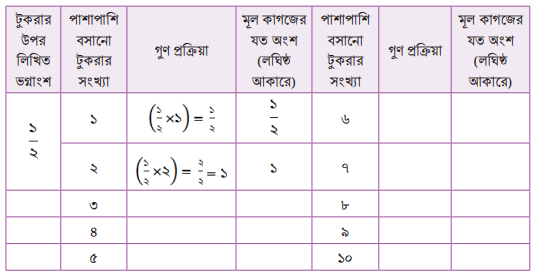
(আংশিক পূর্ণ করা আছে। তোমাদের কাজের মাধ্যমে সম্পুর্ণ করো পরবর্তীতে চিত্রের সাহায্যে ধারণা নিয়ে, নিজের খাতায় ছক এঁকে পাশাপাশি বসানো টুকরার সংখ্যা ১১ হতে ২০ এর জন্য ছক পূরণ করো)
এখন তাহলে কি দেখতে পাচ্ছো? তুমি কিন্তু প্রত্যেকবার একটি করে খণ্ড পাশাপাশি বসাচ্ছো এবং সেটির সাপেক্ষে একটি ভগ্নাংশ বা পূর্ণসংখ্যা পাচ্ছো।
ভাবো তো এই প্রক্রিয়ায় আমরা আসলে কি পাচ্ছি? উদাহরণের ওই – খন্ড থেকে চিন্তা করি। ৩টি – খণ্ড পাশাপাশি বসানো মানে হলো আসলে সেটিকে ৩ দিয়ে গুণ করা। তার মানে আমরা এই কাগজের টুকরা বসানোর খেলা থেকে মূলত আমরা একটি ভগ্নাংশকে একটি পূর্ণ সংখ্যা দ্বারা গুণ করছি। অর্থাৎ, যে কয়টি টুকরা (একই ভগ্নাংশ) পাশাপাশি বসানো হচ্ছে, সেই টুকরার সংখ্যা (যেটি একটি পূর্ণসংখ্যা) দিয়ে ভগ্নাংশটিকে গুণ করা হচ্ছে।
এভাবে আসলে কি পাওয়া যাচ্ছে ভাবো তো? মনে করে দেখো, ধনাত্মক পূর্ণসংখ্যা ক্ষেত্রেও কিন্তু আমরা, কোন নির্দিষ্ট ধনাত্মক পূর্ণসংখ্যাকে এভাবে আরেকটি ধনাত্মক পূর্ণসংখ্যা দিয়ে গুণ করে ওই নির্দিষ্ট ধনাত্মক পূর্ণসংখ্যাটির গুণিতক পেয়েছি। সাধারণ ভগ্নাংশের ক্ষেত্রে যখন এই কাজটি করছি, তখন সেগুলো সাধারণ ভগ্নাংশের গুণিতক হচ্ছে, কারণ গুণিতক বা গুণফলটি কিন্তু একটি ভগ্নাংশ অথবা পূর্ণসংখ্যা হচ্ছে।
অর্থাৎ, একটি ভগ্নাংশের সাথে একটি পূর্ণসংখ্যা গুণ করলে আমরা যে আরেকটি ভগ্নাংশ বা পূর্ণসংখ্যা পাই, সেটিই ওই ভগ্নাংশটির একটি গুণিতক।
এখন তাহলে আমরা নিচের ছকটি পূরণ করে একটি গুণিতক টেবিল তৈরি করে ফেলি। তোমরা প্রতিটি ভগ্নাংশেরই প্রথম ১০ টি করে গুণিতক নির্ণয় করবে। ছকটি আংশিকভাবে পূর্ণ করা হয়েছে।
এভাবেই তুমি চাইলে যেকোনো সাধারণ ভগ্নাংশের গুণিতক নির্ণয় করতে পারবে।
এখন চিন্তা করে দেখো তো, তুমি কি কোন ধনাত্মক পূর্ণসংখ্যার সবগুলো গুণিতক নির্ণয় করতে পারো? পারো না কিন্তু। পূর্বেই জেনে এসেছি ধনাত্মক পূর্ণসংখ্যার গুণিতক অসীমসংখ্যক হতে পারে, যেহেতু ধনাত্মক পূর্ণসংখ্যার সংখ্যা অসীম। তেমনি একইভাবে উপর থেকে কিন্তু তোমরা দেখতে পারছো যে সাধারণ ভগ্নাংশের গুণিতক সংখ্যাও অসীম। কারণ একটি সাধারণ ভগ্নাংশের সাথে আরেকটি পূর্ণসংখ্যা গুণ করলে আমরা সবসময়ই ভগ্নাংশ অথবা পূর্ণসংখ্যা পাই।
