সান্ত ও অনন্ত সেট (Finite and Infinite Sets )

আজকে আমরা আলোচনা করবো  সান্ত ও অনন্ত সেট সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

 

 

সান্ত ও অনন্ত সেট (Finite and Infinite Sets )

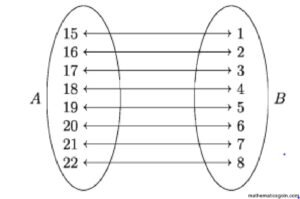
A = {15, 16, 17, 18, 19, 20, 21, 22 ] সেটটির সদস্যগুলো গণনা করে দেখা যায় যে, A সেটের সদস্য সংখ্যা ৪। এই গণনার কাজ A সেটের সঙ্গে B = {1, 2, 3, 4, 5, 6, 7, 8} সেটের একটি এক-এক মিল স্থাপন করে সম্পন্ন করা হয়। যেমন, নিচের চিত্রে দেখানো হয়েছে।

সংজ্ঞা ৩ (সান্ত ও অনন্ত সেট)

গণনা করে যে সকল সেটের সদস্য সংখ্যা নির্ধারণ করা যায়, এদের সান্ত সেট বলা হয়। কোনো সেট A সান্ত সেট না হলে, একে অনন্ত সেট বলা হয়।

ক) ফাঁকা সেট Ø সান্ত সেট, এর সদস্য সংখ্যা 0 ।

খ) যদি কোনো সেট A এবং Jm = {1, 2, 3, …, m} সমতুল হয়, যেখানে m∈N, তবে A একটি সান্ত সেট এবং A এর সদস্য সংখ্যা m

গ) A কোনো সান্ত সেট হলে, A এর সদস্য সংখ্যাকে n(A) দ্বারা সূচিত করা হয়।

দ্রষ্টব্য:

ক) J1 = { 1 }, J2 = {1, 2}, J3 = {1, 2, 3} ইত্যাদি প্রত্যেককেই N এর সান্ত উপসেট বলা হয় এবং n(J1) = 1, n (J2 ) = 2, n( J3 ) = 3 ইত্যাদি। বাস্তবিক পক্ষে, Jm~Jm এবং n (Jm) = m

খ) শুধুমাত্র সান্ত সেটেরই সদস্য সংখ্যা নির্দিষ্ট করা যায়। n(A) লিখলে বুঝতে হবে A সান্ত সেট।
গ) A ও B সমতুল সেট এবং এদের মধ্যে একটি সেট সান্ত হলে অপর সেটটিও সান্ত হবে এবং n(A) = n(B) হবে।

প্রতিজ্ঞা ৬.

যদি A সান্ত সেট হয় এবং B, A এর প্রকৃত উপসেট হয়, তবে B সান্ত সেট এবং n(B) < n (A) হবে।

প্রতিজ্ঞা ৭.

A অনন্ত সেট হবে যদি ও কেবল যদি A ও A এর একটি প্রকৃত উপসেট সমতুল হয়।

দ্রষ্টব্য:

স্বাভাবিক সংখ্যার সেট N একটি অনন্ত সেট।

 

 

সান্ত সেটের উপাদান সংখ্যা

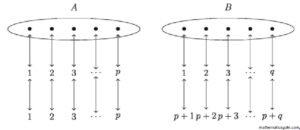
সান্ত সেট A এর উপাদান সংখ্যা n(A) দ্বারা সূচিত করা হয়েছে এবং n(A) নির্ধারণের পদ্ধতি ব্যাখ্যা করা হয়েছে। এবার মনে করি, n(A) = p > 0, n(B) = 9 > 0 যেখানে A ∩B = Ø

উপরের চিত্রে বর্ণিত এক-এক মিল থেকে দেখা যায় যে, AUB ~ Jp+q

অর্থাৎ, n(AUB) = p+ q = n(A) + n(B) । এ থেকে নিচের প্রতিজ্ঞাটি বলা যায়।

প্রতিজ্ঞা ৮.

যদি A ও B পরস্পর নিশ্ছেদ সান্ত সেট হয়, তবে n(AUB) = n(A) + n(B)। এই প্রতিজ্ঞাকে সম্প্রসারণ করে বলা যায় যে, n(AUBUC) = n(A) + n(B) + n(C)। একইভাবে n(AUBUCUD) = n(A) + n(B) + n(C) + n(D) ইত্যাদি, যেখানে A, B, C, D সেটগুলো পরস্পর নিশ্ছেদ সান্ত সেট।

প্রতিজ্ঞা ৯.

যেকোনো সান্ত সেট A ও B এর জন্য n(AUB) = n(A) + n(B) – n (AB)।
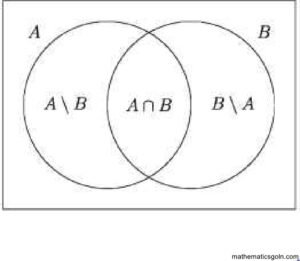
প্রমাণ: এখানে, A\B, AB এবং B\A সেট তিনটি পরস্পর নিশ্ছেদ সেট [ভেনচিত্র দ্রষ্টব্য]।

 

 

ফলে A = (A\ B) U (A∩B) এবং B= (B\A) U (A∩B)

AUB (A\B) U (A∩B) u (B\A)

n(A) = n(A \ B) +n(A∩B) ………(1)

n(B) = n(B \ A) +n(Aп B) ………… (2)

n(AUB) = n(A\B) + n(A∩ B) + n(B\ A) ………(3)

সুতরাং, (1) নং থেকে পাই, n(A \ B) = n(A) – n(A∩B)

এবং (2) নং থেকে পাই, n (B \ A) = n(B) – n(A∩B)

এখন, n (A \ B) এবং n(B \ A) (3) এ বসিয়ে পাই,

n(AUB) = n(A) — n(A∩B) + n(B) – n(A∩B) +n(A∩B)

n(AUB) = n(A) + n(B) − n(A∩B)

 

 

আরও দেখুনঃ

• গনিতের সেট