আজকে আমরা আলোচনা করবো সার্বিক ফাংশন সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
সার্বিক ফাংশন (Onto Function)
একটি সার্বিক ফাংশন হলো এমন এক ধরনের ফাংশন যার প্রতিবিম্বসমূহ এর কোডমেইনের সমান। একইভাবে , একটি ফাংশন f
ডোমেইন X এবং কোডোমেইন Y সহ সার্বিক হবে যদি Y এর অন্তর্ভুক্ত প্রত্যেক y এর জন্য অন্তত একটি x এর মধ্যে বিদ্যমান থাকে যাতে f(x)=y হয়।সা-র্বিক ফাংশনসমূহকে অনেক সময় দুই মাথা বিশিষ্ট ডানদিকবর্তী তীর দ্বারা চিহ্নিত করা হয়।
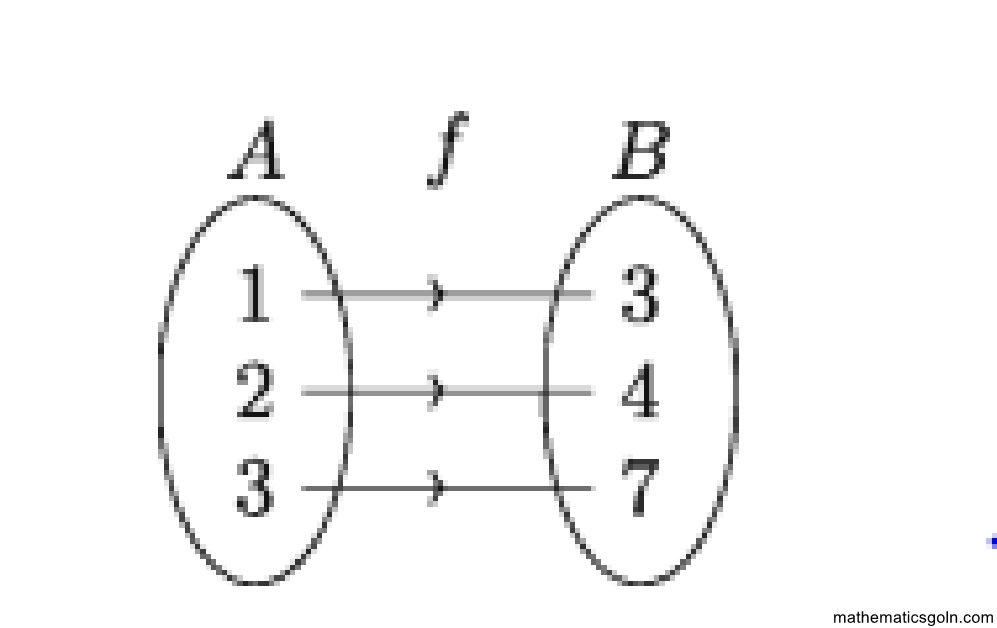
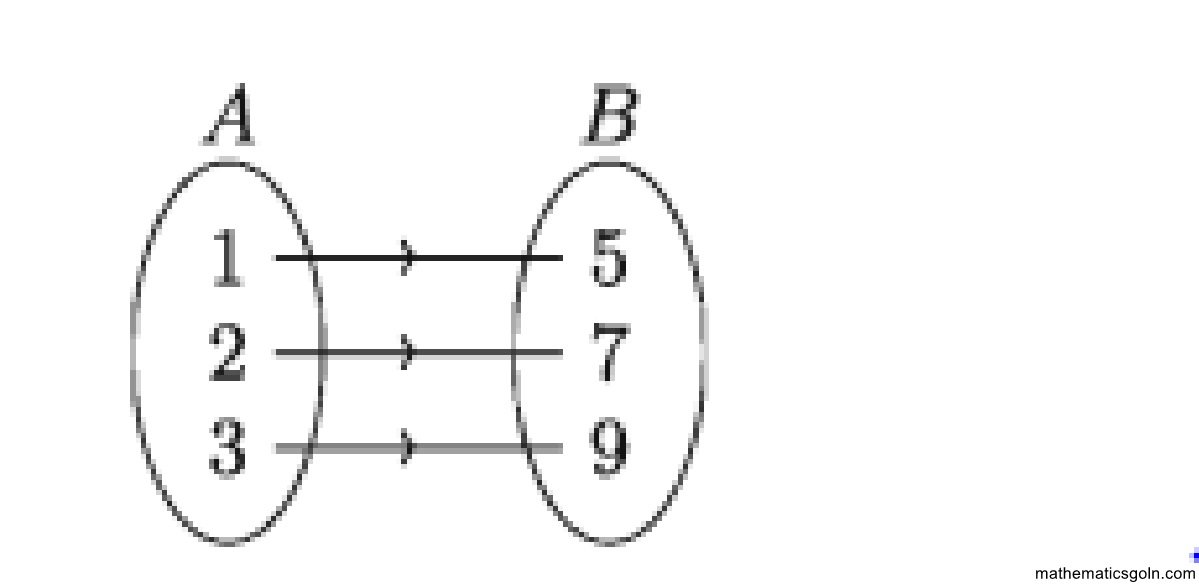
চিত্রে ফাংশন f এর অধীনে সেট A = {1,2,3} এবং B {5,7,9} বিবেচনা করি যেখানে = 1 → 5, 2 → 7 এবং 3 → 9 অর্থাৎ B এর প্রত্যেক উপাদান A সেটের একটি উপাদানের প্রতিবিম্ব। এইরূপ ফাংশনকে সার্বিক ফাংশন বলা হয়।
যেকোন ফাংশন সার্বিক সেটে রূপান্তরিত হয় এর কোডোমেনকে ডোমেইনের উপাদানসমূহের প্রতিবিম্বের মধ্যে সীমাবদ্ধ রেখে। প্রত্যেক সা-র্বিক ফাংশন এর একটি ডান বিপরীত রয়েছে এবং ডান বিপরীতসহ প্রত্যেক ফাংশন অবশ্যই সা-র্বিক ফাংশন হবে। সা-র্বিক ফাংশনের কম্পোজিট(একের অধিক ফাংশনের সংমিশ্রণ ) সর্বদাই সা-র্বিক ফাংশন হয়ে থাকে। যেকোনো ফাংশনকে সা-র্বিক ফাংশন এবং একক ফাংশনে বিভক্ত করা যেতে পারে।
সংজ্ঞা ১১ (সার্বিক ফাংশন)
একটি ফাংশন f : A→B কে সা-র্বিক ফাংশন (onto function) বলা হবে যদি প্রত্যেক b∈ B এর জন্য একটি a ∈ A পাওয়া যায় যেন f(a) = b হয়। অর্থাৎ B = রেঞ্জ f ।
উদাহরণ ৩৪.
যদি f : R → R এবং g : R → R ফাংশন দুইটি f(x) = x + 5 এবং g(x) = x 5 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, f এর বিপরীত ফাংশন g।
সমাধান:
f ফাংশনটি এক-এক, কেননা
f(x1) = f(x2) হলে 1 + 5 = x2 +5 বা, x1 = x2 ।
আবার, f ফাংশনটি সার্বিক, কেননা
y = f(x) হলে x + 5 = y বা, x = y – 5 ∈R
সুতরাং বিপরীত ফাংশন f-1 বিদ্যমান।
f¯1(x) = y হলে f(y) = x বা, y + 5 = x বা, y = x – 5
আবার, f-1(x) = x – 5 = g ( x )
f-1 ও g উভয়ের ডোমেন একই হওয়ায় f−1 = g
ফাংশনের সীমা ঃ
ফাংশনের সীমা : গাণিতিক সমস্যা ঃ

১ thought on “সার্বিক ফাংশন (Onto Function)”