আজকে আমাদের আলোচনার বিষয়ঃ সুষম বহুভুজের ক্ষেত্রফল । এটি নবম – দশম শ্রেনী গণিতের পরিমিতি অংশের অন্তর্গত।

সুষম বহুভুজের ক্ষেত্রফল
সুষম বহুভুজের বাহুগুলোর দৈর্ঘ্য সমান। আবার কোণগুলোও সমান। n সংখ্যক বাহুবিশিষ্ট সুষম বহুভুজের কেন্দ্র ও শীর্ষবিন্দুগুলো যোগ করলে n সংখ্যক সমদ্বিবাহু ত্রিভুজ উৎপন্ন হয়।
সুতরাং বহুভুজের ক্ষেত্রফল = n x একটি ত্রিভুজক্ষেত্রের ক্ষেত্রফল
ABCDEF … একটি সুষম বহুভুজ, যার কেন্দ্র O, বাহু, n সংখ্যক এবং প্রতি বাহুর দৈর্ঘ্য a। O, A; O, B যোগ করি।
ধরি ∆AOB এর উচ্চতা ON = h এবং ∠OAB = 0 সুষম বহুভুজের প্রতিটি শীর্ষে উৎপন্ন কোণের পরিমান = 20 . সুষম বহুভুজের n সংখ্যক শীর্ষ কোণের সমষ্টি = 20n

সুষম বহুভুজের কেন্দ্রে উৎপন্ন কোণের পরিমান = 4 সমকোণ
.: কেন্দ্রে উৎপন্ন কোণ ও n শীর্ষ কোণের সমষ্টি (20n + 4) সমকোণ।
∆OAB এর তিন কোণের সমষ্টি = 2 সমকোণ
এরূপ n সংখ্যক ত্রিভুজের কোণগুলোর সমষ্টি 2n সমকোণ
20 .n + 4 সমকোণ = 2n সমকোণ
বা, 20. n = ( 2n – 4 ) সমকোণ
বা, 0 = ( 2n – 4 )/2n = সমকোণ
বা, 0 = (1-2/n) x 90°
0 = 90° – 180°/n
এখানে, tan0 = ON/AN = h/a/2 = 2h/a
.:. h = a/2tane
∆OAB এর ক্ষেত্রফল = 1/2ah
= 1/2a × a/2tane
= a²/4tan(90° – 180°/n)
= a²/4 cot 180°/ n = [ tan ( 90° – A) = cotA]
n সংখ্যক বাহুবিশিষ্ট সুষম বহুভুজের ক্ষেত্রফল = na2/4 cot180°/n
উদাহরণ ১৫.
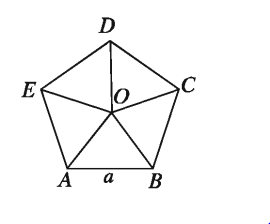
একটি সুষম পঞ্চভুজের প্রতিবাহুর দৈর্ঘ্য 4 সে.মি. হলে, এর ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, সুষম পঞ্চভুজের বাহুর দৈর্ঘ্য a = 4 সে.মি.। বাহুর সংখ্যা n = 5
আমরা জানি, সুষম বহুভুজের ক্ষেত্রফল na²/cot 180°/n
সুষম পঞ্চভুজের ক্ষেত্রফল = (5 x 42)/cot180°/4বর্গ সে.মি.
= 20 x cot36° বর্গ সে.মি.
= 20 × 1.376 বর্গ সে.মি. (ক্যালকুলেটরের সাহায্যে)
= 27.528 বর্গ সে.মি. (প্রায়)
নির্ণেয় ক্ষেত্রফল 27.528 বর্গ সে. মি. (প্রায়)
উদাহরণ ১৬
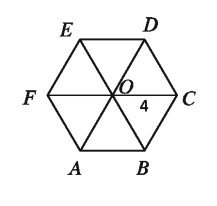
একটি সুষম ষড়ভুজের কেন্দ্র থেকে কৌণিক বিন্দুর দূরত্ব 4 মিটার হলে, এর ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, ABCDEF একটি সুষম ষড়ভুজ। এর কেন্দ্র O থেকে শীর্ষবিন্দুগুলো যোগ করা হলো। ফলে 6 টি সমান ক্ষেত্রবিশিষ্ট ত্রিভুজ উৎপন্ন হয়।
∠COD = 360°/6 = 60°
মনে করি কেন্দ্র থেকে শীর্ষবিন্দুগুলোর দূরত্ব a মিটার।
∆COD এর ক্ষেত্রফল = 1/2.a. asin 60°
= √3/4 × 42 বর্গ মিটার = 4√3 বর্গ মিটার
সুষম ষড়ভুজক্ষেত্রের ক্ষেত্রফল = 6 × ACOD এর ক্ষেত্রফল
= 6 × 4√3 বর্গ মিটার = 24/3 বর্গ মিটার
নির্ণেয় ক্ষেত্রফল 24√3 বর্গ মিটার
উদাহরণ ১৭.
প্রদত্ত চিত্রের আলোকে
ক) আয়তক্ষেত্রটির কর্ণের দৈর্ঘ্য নির্ণয় কর।
খ) ক্ষেত্রটির ক্ষেত্রফল পূর্ণসংখ্যায় নির্ণয় কর।
গ) সমদ্বিবাহু ত্রিভুজের গ্রহণযোগ্য পরিসীমা নির্ণয় কর।

সমাধান :
ক) চিত্র অনুসারে, ক্ষেত্রটি ABCD আয়তক্ষেত্র এবং ADE সমদ্বিবাহু ত্রিভুজক্ষেত্রে বিভক্ত। ABCD আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য = √(502 + 142) সে.মি. = 51.92 সে.মি. (প্রায়)
খ) আয়তক্ষেত্র ABCD এর ক্ষেত্রফল 50 x 14 বর্গ সে.মি. = 700 বর্গ সে.মি.
ত্রিভুজক্ষেত্র ADE এর ক্ষেত্রফল = 1/2AD.AE. sin∠DAE = 1/2 x 50 x 50 x sin73.74° বর্গ সে.মি. = 24 x 50 x 0.960001 বর্গ সে.মি. = 1200 বর্গ সে.মি. (প্রায়)
সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল = ( 700 + 1200) বর্গ সে.মি. 1900 বর্গ সে.মি.

গ) ∆ADE এ AD = AE = 50 সে.মি. = a (ধরি), DE = b (ধরি)
সমদ্বিবাহু ত্রিভুজ ADE এর ক্ষেত্রফল = b/4√(4a2 – b2)
প্রশ্নানুসারে, b/4√(4a2 – b2) = 1200
b/4 √(50) 2 – b2) = 4800
বা, b2 ( 10000 – b2 ) = 23040000 [বর্গ করে]
বা, 10000b2 – b4 = 23040000
বা, b4 – 10000b2 + 23040000 = 0
বা, b4 – 6400b2 – 3600b2 + 2304000 = 0
বা, (b2 – 6400) (b2 – 3600 ) = 0
b² – 6400 = 0 অথবা 62 – 3600 = 0
বা, b2 = 6400 অথবা 62 = 3600
b = 80 অথবা b = 60
b = 80 হলে, 1/2AD.DE sin∠ADE = 1200
বা, 1/2x 50 x 80 x sin∠ADE = 1200
বা, sin∠ADE = 0.6
∠ADE = 36.87° (প্রায়)
∆ADE এর তিন কোণের সমষ্টি = 73.74°36.87° +36.87° = 147.48°
কিন্তু ত্রিভুজের তিন কোণের সমষ্টি = 180°, সুতরাং b ≠ 80
b = 60 হলে, 1/2AD. DE sin∠ADE = 1200
বা, 1/2 x 50 x 60 x sin∠ADE = 1200 2
বা, sin∠ADE = 0.8
∠ADE = 53.13° (প্রায়)
∆ADE এর তিন কোণের সমষ্টি = 73.74° + 53.13° + 53.13° = 180°, সুতরাং b = 60
ত্রিভুজটির পরিসীমা (50+50 + 60 ) সে.মি. = 160 সে.মি.