আজকে আমাদের আলোচনার বিষয়ঃ সেটের প্রকারভেদ । এটি অষ্টম শ্রেনী গণিতের সেট এর অন্তর্গত।

সেটের প্রকারভেদ
সসীম সেট (Finite set)
যে সেটের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায়, একে সসীম সেট বলে। যেমন A = {a,b,c,d}, B = { 5, 10, 15, 100, ইত্যাদি সসীম সেট। এখানে A সেটে 4টি উপাদান এবং B সেটে 20 টি উপাদান আছে ।
অসীম সেট (Infinite set)
যে সেটের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায় না, একে অসীম সেট বলে । অসীম সেটের একটি উদাহরণ হলো স্বাভাবিক সংখ্যার সেট, N = {1, 2, 3, 4,…}। এখানে, N সেটের উপাদান সংখ্যা অসংখ্য যা গণনা করে নির্ধারণ করা যায় না । এই শ্রেণিতে শুধু সসীম সেট নিয়ে আলোচনা করা হবে ।

ফাঁকা সেট (Empty set)
যে সেটের কোনো উপাদান নেই একে ফাঁকা সেট বলে । ফাঁকা সেটকে Ø প্রতীক দ্বারা প্রকাশ করা হয় ।
ভেনচিত্র (Venn-diagram)
জন ভেন (১৮৩৪–১৮৮৩) চিত্রের সাহায্যে সেট প্রকাশ করার রীতি প্রবর্তন করেন । এই চিত্রগুলো তাঁর নামানুসারে ভেনচিত্র নামে পরিচিত । ভেনচিত্রে সাধারণত আয়তাকার ও বৃত্তাকার ক্ষেত্র ব্যবহার করা হয় । নিচে কয়েকটি সেটের ভেনচিত্র প্রদর্শন করা হলো :
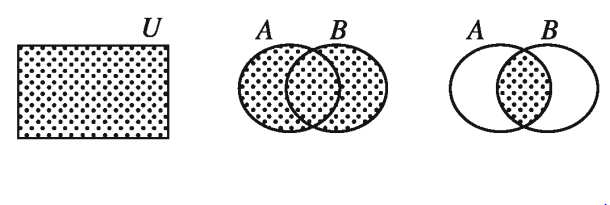
ভেনচিত্র ব্যবহার করে অতি সহজে সেট ও সেট প্রক্রিয়ার বিভিন্ন বৈশিষ্ট্য যাচাই করা যায় ।
উপসেট (Subset)
মনে করি, A = {a,b} একটি সেট । A সেটের উপাদান নিয়ে আমরা {a,b},{a},{b} সেটগুলো গঠন করতে পারি । গঠিত {a,b},{a},{b} সেটগুলো A সেটের উপসেট ।
কোনো সেটের উপাদান থেকে যতগুলো সেট গঠন করা যায় এদের প্রত্যেকটি প্রদত্ত সেটের উপসেট । ফাঁকা সেট যেকোনো সেটের উপসেট ।
যেমন : P = {2, 3, 4, 5} এবং Q = { 3, 5} হলে, Q সেটটি P সেটের উপসেট। অর্থাৎ Q⊆P.
কারণ Q সেটের 3 এবং 5 উপাদানসমূহ P সেটে বিদ্যমান। ‘⊆’ প্রতীক দ্বারা উপসেটকে সূচিত করা হয় ।
উদাহরণ ৪ ।
A = {1, 2, 3} এর উপসেটসমূহ লেখ ।
সমাধান :
A সেটের উপসেটসমূহ নিম্নরূপ : {1, 2, 3}, {1, 2}, {1,3}, {2, 3}, {1}, {2}, {3},Ø
সার্বিক সেট (Universal Set)
আলোচনায় সংশ্লিষ্ট সকল সেট যদি একটি নির্দিষ্ট সেটের উপসেট হয় তবে ঐ নির্দিষ্ট সেটকে এর উপসেটগুলোর সাপেক্ষে সার্বিক সেট বলে । সার্বিক সেটকে U প্রতীক দ্বারা সূচিত করা হয় । যেমন: কোনো বিদ্যালয়ের সকল শিক্ষার্থীর সেট হলো সার্বিক সেট এবং অষ্টম শ্রেণির শিক্ষার্থীদের সেট উক্ত সার্বিক সেটের উপসেট ।
সকল সেট সার্বিক সেটের উপসেট ।
উদাহরণ ৫।
A = {1, 2, 3, 4, 5, 6}, B = {1, 3, 5}, C = {3, 4, 5, 6} হলে, সার্বিক সেট নির্ণয় কর । সমাধান : দেওয়া আছে, A = {1, 2, 3, 4, 5, 6}, B = {1, 3, 5}, C = { 3, 4, 5, 6} এখানে, B সেটের উপাদান 1, 3, 5 এবং C সেটের উপাদান 3, 4, 5, 6 যা A সেটে বিদ্যমান ।
B এবং C সেটের সাপেক্ষে সার্বিক সেট A
পূরক সেট (Complement of a set)
যদি U সার্বিক সেট এবং A সেটটি U এর উপসেট হয় তবে, A সেটের বহির্ভূত সকল উপাদান নিয়ে যে সেট গঠন করা হয়, একে A সেটের পূরক সেট বলে। A এর পূরক সেটকে A বা A’ দ্বারা প্রকাশ করা হয় ।
মনে করি, অষ্টম শ্রেণির 60 জন শিক্ষার্থীর মধ্যে 9 জন অনুপস্থিত । অষ্টম শ্রেণির সকল শিক্ষার্থীদের সেট সার্বিক সেট বিবেচনা করলে উপস্থিত (60–9) বা 51 জনের সেটের পূরক সেট হবে অনুপস্থিত 9 জনের সেট ।
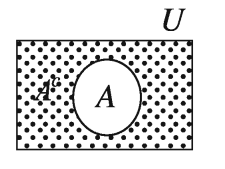
উদাহরণ ৬ ।
U = {1, 2, 34, 5, 6} এবং A = {2, 4, 6} হলে AS নির্ণয় কর ।
সমাধান :
দেওয়া আছে, U = {1, 2, 3, 4, 5, 6} এবং A = {2, 4, 6}
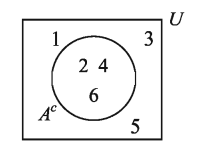
Ac = A এর পূরক সেট
= A এর বহির্ভূত উপাদানসমূহের সেট
= {1, 3, 5}
নির্ণেয় সেট A = {1, 3, 5}
