সেটের সেট প্রক্রিয়া

আজকে আমাদের আলোচনার বিষয়ঃ সেটের সেট প্রক্রিয়া । এটি অষ্টম শ্রেনী গণিতের সেট এর অন্তর্গত।

 

 

সেটের সেট প্রক্রিয়া

সংযোগ সেট (Union of Sets )

মনে করি, P = {2, 3, 4} এবং Q = {4, 5, 6}. এখানে P এবং Q সেটের অন্তর্ভুক্ত উপাদানসমূহ 2, 3, 4, 5, 6 P ও Q সেটের সকল উপাদান নিয়ে গঠিত সেট {2, 3, 4, 5, 6, যা P ও Q সেটদ্বয়ের সংযোগ সেট ।

দুই বা ততোধিক সেটের সকল উপাদান নিয়ে গঠিত সেটকে সংযোগ সেট বলা হয় ।

 

 

ধরি, A ও B দুইটি সেট। A ও B এর সংযোগ সেটকে AUB দ্বারা প্রকাশ করা হয় এবং পড়া হয় A সংযোগ B অথবা ‘ A union B.
সেট গঠন পদ্ধতিতে AUB = {x: x ∈ A অথবা x ∈ B }

উদাহরণ ৭।

C = {রাজ্জাক, সাকিব, অলোক} এবং D = {অলোক, মুশফিক} হলে, CUD নির্ণয় কর । সমাধান : দেওয়া আছে, C = {রাজ্জাক, সাকিব, অলোক} এবং D = {অলোক, মুশফিক}

:: CUD = {রাজ্জাক, সাকিব, অলোক} U {অলোক, মুশফিক}

= {রাজ্জাক, সাকিব, অলোক, মুশফিক}

উদাহরণ ৮।

R = {x: x, 6-এর গুণনীয়কসমূহ} এবং S = {x : x, 8 -এর গুণনীয়কসমূহ } হলে, RUS নির্ণয় কর।

 

 

সমাধান :

দেওয়া আছে, R = {x : x, 6-এর গুণনীয়কসমূহ} = {1,2,3,6}

এবং S = {x : x, 8 এর গুণনীয়কসমূহ}

={1, 2,4,8}

.. RUS = {1, 2, 3, 6} U {1, 2, 4, 8} = {1, 2, 3, 4, 6, 8}

ছেদ সেট (Intersection of sets)

মনে করি, রিনা বাংলা ও আরবি ভাষা পড়তে ও লিখতে পারে এবং জয়া বাংলা ও হিন্দি ভাষা পড়তে ও লিখতে পারে । রিনা যে ভাষা পড়তে ও লিখতে পারে এদের সেট {বাংলা, আরবি} এবং জয়া যে ভাষা পড়তে ও লিখতে পারে এদের সেট {বাংলা, হিন্দি} । লক্ষ করি, রিনা ও জয়া প্রত্যেকে যে ভাষা পড়তে ও লিখতে পারে তা হচ্ছে বাংলা এবং এর সেট {বাংলা} । এখানে {বাংলা} সেটটি ছেদ সেট ।

দুই বা ততোধিক সেটের সাধারণ (Common) উপাদান নিয়ে গঠিত সেটকে ছেদ সেট বলা হয় ।

ধরি, A ও B দুইটি সেট। A ও B এর ছেদ সেটকে AB দ্বারা প্রকাশ করা হয় এবং পড়া হয় A ছেদ B. সেট গঠন পদ্ধতিতে A∩B={x:x∈ A এবং x ∈ B }

উদাহরণ ৯।

A = {1,3,5} এবং B = {5, 7} হলে, A∩B নির্ণয় কর ।

 

 

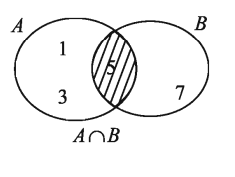
সমাধান :

দেওয়া আছে, A = {1, 3, 5} এবং B = {5, 7}

A∩B = {1, 3, 5} ∩ {5, 7} = {5}

উদাহরণ ১০।

P = {x: x, 2 এর গুণিতক এবং x ≤ 8} এবং Q = {x: x, 4 এর গুণিতক এবং x≤12} হলে, P∩Q নির্ণয় কর ।

সমাধান :

দেওয়া আছে, P = {x : x, 2 এর গুণিতক এবং x ≤ 8} = {2,4,6,8} এবং Q = {x : x, 4 এর গুণিতক x ≤12} = {4, 8, 12}

P∩Q = {2, 4, 6, 8} ∩ {4, 8, 12} = {4, 8}

নিশ্ছেদ সেট (Disjoint sets )

মনে করি, বাংলাদেশের পাশাপাশি দুইটি গ্রাম । একটি গ্রামের কৃষকগণ জমিতে ধান ও পাট চাষ করেন এবং অপর গ্রামের কৃষকগণ জমিতে আলু ও সবজি চাষ করেন । চাষকৃত ফসলের সেট দুইটি বিবেচনা করলে পাই {ধান, পাট} এবং {আলু, সবজি} । উক্ত সেট দুইটিতে ফসলের কোনো মিল নেই। অর্থাৎ, দুই গ্রামের কৃষকগণ একই জাতীয় ফসল চাষ করেন না। এখানে সেট দুইটি পরস্পর নিশ্ছেদ সেট ।

 

 

যদি দুইটি সেটের উপাদানগুলোর মধ্যে কোনো সাধারণ উপাদান না থাকে, তবে সেট দুইটি পরস্পর নিশ্ছেদ সেট ।

ধরি, A ও B দুইটি সেট । A ও B পরস্পর নিশ্ছেদ সেট হবে যদি AB = Ø হয়। দুইটি সেটের ছেদ সেট ফাঁকা সেট হলে সেটদ্বয় পরস্পর নিশ্ছেদ সেট ।

উদাহরণ ১১।

A = {x : x, বিজোড় স্বাভাবিক সংখ্যা এবং 1<x<7} এবং B = {x : x, 8 এর গুণনীয়কসমূহ} হলে, দেখাও যে, A ও B সেটদ্বয় পরস্পর নিশ্ছেদ সেট ।

সমাধান :

দেওয়া আছে, A = {x : x, বিজোড় স্বাভাবিক সংখ্যা এবং 1<x<7}

= {3,5}

এবং B = {x : x, 8 এর গুণনীয়কসমূহ}

= {1, 2, 4, 8}

A∩B = {3,5}∩ {1, 2, 4, 8}

= Ø

A ও B সেটদ্বয় পরস্পর নিশ্ছেদ সেট ।

উদাহরণ ১২ ।

C = {3, 4, 5} এবং D = {4, 5, 6} হলে, CUD এবং C∩D নির্ণয় কর ।

 

 

সমাধান :

দেওয়া আছে, C = { 3, 4, 5} এবং D = { 4, 5, 6}

CUD = { 3, 4, 5}∩ { 4, 5, 6} = { 3, 4, 5, 6}

এবং C∩D = {3, 4, 5}∩ {4, 5, 6} = {4, 5}

উদাহরণ ১৩ ।

E = {x : x, মৌলিক সংখ্যা এবং x < 30} সেটটি তালিকা পদ্ধতিতে প্রকাশ কর ।

সমাধান :

নির্ণেয় সেটটি হবে 30 অপেক্ষা ছোট মৌলিক সংখ্যাসমূহের সেট ।

এখানে, 30 অপেক্ষা ছোট মৌলিক সংখ্যাসমূহ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 নির্ণেয় সেট = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}

উদাহরণ ১৪।

A ও B যথাক্রমে 42 ও 70 এর সকল গুণনীয়কের সেট হলে, A∩B নির্ণয় কর ।

সমাধান :

এখানে, 42 = 1× 42 = 2 x 21 = 3×14 = 6×7

42 এর গুণনীয়কসমূহ 1, 2, 3, 6, 7, 14, 21, 42

A= {1, 2, 3, 6, 7, 14, 21, 42}

আবার, 70 = 1x 70 = 2 x 35 = 5×14 = 7×10

70 এর গুণনীয়কসমূহ 1, 2, 5, 7, 10, 14, 35, 70

B={1, 2, 5, 7, 10, 14, 35, 70}

A∩B={1,2,3,6,7,14,21,42}∩{1,2,5,7,10,14,35,70} = {1, 2, 7, 14}