সেট ও ফাংশন অনুশীলনী ১

আজকের আলোচনার বিষয়ঃ  অধ্যায় ১ অনুশীলনী ১ । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

 

 

সেট ও ফাংশন অনুশীলনী ১

 

১. (i) কোন সেটের সদস্য সংখ্যা 2n হলে, এর উপসেটের সংখ্যা হবে 4^n।

(ii) সকল মূলদ সংখ্যার সেট Q = {p/q: P,q ∈ Z},

(iii) a, b ∈ R; (a,b) = {x: x ∈ R এবং a < x < b}

উপরের উক্তিগুলোর আলোকে নিচের কোনটি সঠিক?

ক) i ও ii
খ) ii ও iii
গ) i ও iii
ঘ) i, ii ও iii

প্রত্যেক n ∈ N এর জন্য An = {n, 2n, 3n, … } হলে (২ – ৪) নং প্রশ্নের উত্তর দাও:

২. A1 ∩ A2 এর সমান নিচের কোনটি?

ক) A1
খ) A2
গ) A3
ঘ) A4

৩. নিচের কোনটি A3∩ A6 এর সমান ?

ক) A2
খ) A3
গ) A4
ঘ) As

8. A2 ∩ A3 এর পরিবর্তে নিচের কোনটি লেখা যায়?

ক) As
খ) A4
গ) As
ঘ) Ag

 

৫. দেওয়া আছে U = {x : 1 ≤ x ≤ 20, x ∈ Z}, A = {x : x বিজোড় সংখ্যা} এবং = B = {x : x মৌলিক সংখ্যা}। নিম্নের সেটগুলো তালিকা পদ্ধতিতে লিপিবদ্ধ কর:

ক) A
খ) B
গ) C = {x: x ∈ A এবং x ∈ B }
ঘ) D = {x : x ∈ A অথবা x ∈ B }

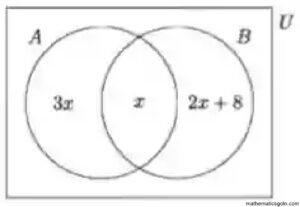
৬. ভেনচিত্রে A ও B সেটের উপাদানগুলোর সংখ্যা দেখানো হয়েছে। যদি n (A) = n(B) হয়, তবে নির্ণয় কর

ক) x এর মান
খ) n(AUB)
গ) n (B \ A) ।

চিত্র

৭. যদি U = {x : x ধনাত্মক পূর্ণসংখ্যা}, A = {x : x > 5} C U এবং B = {x : 5x < 12} CU তবে n(A∩ B) এবং n(AUB) এর মান নির্ণয় কর।

৮. যদি U = {x : x জোড় পূর্ণসংখ্যা}, A = {x : 3x > 25 } C U এবং B = {2:52< 12} C U হয়, তাহলে n(A∩B) এবং n (A’n B’) এর মান নির্ণয় কর।

৯. দেখাও যে, ক) A \ A =∅ খ) A \ ( A \ A) = A

১০. দেখাও যে, A x (BUC) = (A x B ) ( A x C)।

১১. যদি A ⊂ B এবং C ⊂ D হয়, তবে দেখাও যে, (A x C) ⊂ (B × D ) ।

১২. দেখাও যে, A = {1,2,3,n} এবং B = {1,2, 2^2, …, 2^n−1} সেট দুইটি সমতুল।

১৩. দেখাও যে, স্বাভাবিক সংখ্যাসমূহের বর্গের সেট {1, 4, 9, 16, 25, 36, … } একটি অনন্ত সেট।

১৪. প্রমাণ কর যে, n(A) = p, n(B) = q এবং A∩B = Ø হলে, n(AUB) = p+ q

১৫. প্রমাণ কর যে, A, B, C সান্ত সেট হলে, n(AUBUC) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n (CA) + n(A∩B∩C)।

১৬. A = {a, b, x} এবং B = {c, y} সার্বিক সেট U = {a, b, c, x, y, z} এর উপসেট হলে,

ক) যাচাই কর যে, (i) A⊂B’ (ii) AUB’ = B’ (i) A’∩B = B

খ) নির্ণয় কর: (A∩B) U ( A∩B’ ) ।

১৭. কোনো শ্রেণির 30 জন শিক্ষার্থীর মধ্যে 19 জন অর্থনীতি, 17 জন ভূগোল, 11 জন পৌরনীতি, 12 জন অর্থনীতি ও ভূগোল, 4 জন পৌরনীতি ও ভূগোল, 7 জন অর্থনীতি ও পৌরনীতি এবং 3 জন তিনটি বিষয়ই নিয়েছে। কতজন শিক্ষার্থী তিনটি বিষয়ের কোনটিই নেয়নি?

 

 

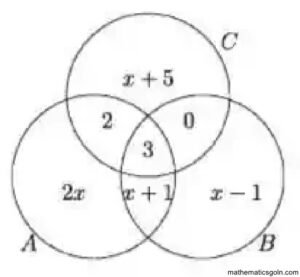
১৮. নিচের ভেনচিত্রে সার্বিক সেট U = AUBUC

ক) যদি n(A∩B) = n(B∩C) হয়, তবে এর মান নির্ণয় কর।

খ) যদি n(B∩C”) = n(A∩C) হয়, তবে y এর মান নির্ণয় কর।

গ) n (U) এর মান নির্ণয় কর।

১৯. নিচের ভেনচিত্রে U = AUBUC এবং n (U) = 50।

ক) x এর মান নির্ণয় কর।
খ) n(B∩C’) এবং n (A’∩B) এর মান নির্ণয় কর।
গ) n(A∩B∩C”) এর মান নির্ণয় কর।

২০. তিনটি সেট A, B এবং C এমনভাবে দেওয়া আছে যেন, A∩B = 0, A∩C = Ø এবং C⊂B। ভেনচিত্র অঙ্কন করে সেটগুলোর ব্যাখ্যা দাও।

২১. দেওয়া আছে A {x : 2 < x ≤ 5, x ∈ R }, B {x : 1 < x < 3, x ∈ R} এবং = = C = {2, 4,5}। নিম্নের সেটগুলো সেট গঠন পদ্ধতিতে প্রকাশ কর:

ক) A∩B
খ) A’∩B’
গ) A’UB

২২. দেওয়া আছে U = {x : x < 10, x ∈ R}, A = {x : 1 < x < 4} এবং B = {x :3 < x < 6}। নিচের সেটগুলো সেট গঠন পদ্ধতিতে প্রকাশ কর:

ক) A∩B
খ) A∩B
গ) A∩B
ঘ) A’∩B’

২৩. নিম্নে প্রতিক্ষেত্রে A ও B সেট দেওয়া আছে, AUB নির্ণয় কর এবং যাচাই কর যে A ⊂ (AUB) এবং B ⊂ (AUB)

ক) A = { – 2 – 1, 0, 1, 2} এবং B = {- 3,0,3}
খ) _ A = {x : x ∈ N, x < 10 এবং x, 2 এর গুণিতক} এবং B = {x : x ∈ N, ∝ < 10 এবং x, 3 এর গুণিতক }

২৪. নিম্নের প্রতিক্ষেত্রে AnB নির্ণয় কর এবং যাচাই কর যে, (A∩B) CA এবং (AnB) ⊂ B

ক) A = {0, 1, 2, 3}, B = {- 1,0, 2}
খ) A = {a, b, c, d}, B = { b, a, c, y}

২৫. বেগম রোকেয়া কলেজের ছাত্রীদের মধ্যে বিচিত্রা, সন্ধানী ও পূর্বাণী পত্রিকার পাঠ্যাভ্যাস সম্পর্কে পরিচালিত এক সমীক্ষায় দেখা গেল 60% ছাত্রী বিচিত্রা, 50% ছাত্রী সন্ধানী, 50% ছাত্রী পূর্বাণী, 30% ছাত্রী বিচিত্রা ও সন্ধানী, 30% ছাত্রী বিচিত্রা ও পূর্বাণী, 20% ছাত্রী সন্ধানী ও পূর্বাণী এবং 10% ছাত্রী তিনটি পত্রিকাই পড়ে।

ক) শতকরা কতজন ছাত্রী উক্ত পত্রিকা তিনটির কোনটিই পড়ে না?
খ) শতকরা কতজন ছাত্রী উক্ত পত্রিকাগুলোর মধ্যে কেবল দুইটি পড়ে?

 

 

২৬. A = {x : x ∈ R এবং x2 – (a + b) x + ab = 0}, B = {1, 2} এবং C = {2, 4, 5}

ক) A সেটের উপাদানসমূহ নির্ণয় কর।

খ) দেখাও যে, P (BAC) = P(B) P(C)।

গ) প্রমাণ কর যে, A x (BUC) = ( A × B) U (A × C) ।

২৭. একটি শ্রেণির 100 জন ছাত্রের মধ্যে 42 জন ফুটবল, 46 জন ক্রিকেট এবং 39 জন দাবা খেলে। এদের মধ্যে 13 জন ফুটবল ও ক্রিকেট, 14 জন ক্রিকেট ও দাবা এবং 12 জন ফুটবল ও দাবা খেলতে পারে। এছাড়া 7 জন কোনো খেলায় পারদর্শী নয়।

ক) উল্লিখিত তিনটি খেলায় পারদর্শী এমন ছাত্রদের সেট এবং কোনো খেলায় পারদর্শী নয় এমন ছাত্রদের সেট ভেনচিত্রে দেখাও।

খ) কতজন ছাত্র উল্লিখিত তিনটি খেলায়ই পারদর্শী তা নির্ণয় কর।

গ) কতজন ছাত্র কেবলমাত্র একটি খেলায় পারদর্শী? কতজন অন্তত দুইটি খেলায় পারদর্শী?

২৮. P(Ø), P({}) সেট নির্ণয় কর।

২৯. এক গ্রামে এক মিস্ত্রী ছিল। সে তাদের ঘর তৈরি করতো যারা নিজেরা নিজেদের ঘর তৈরি করতো না। মিস্ত্রীর ঘর কে তৈরি করতো?

৩০. A = {x : x ∈ A} । সেট A নিয়ে বিস্তৃত আলোচনা কর।