আজকে আমরা আলোচনা করবো সেট ও ফাংশন ১ অনুশীলনী ২ । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
সেট ও ফাংশন অনুশীলনী ২
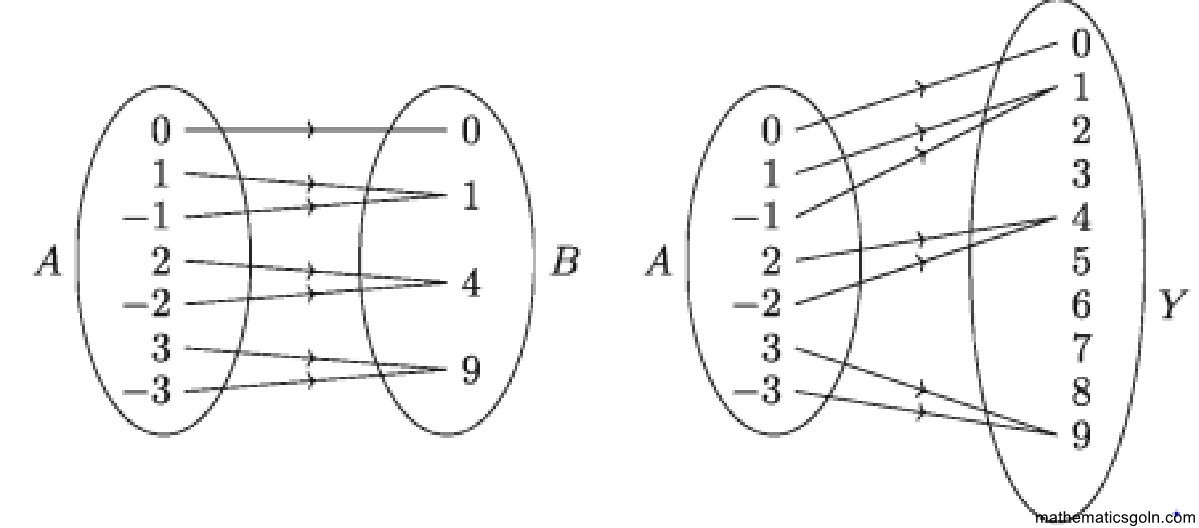
১. {(2, 2), (1, 2), (2, 10), (7, 7)} অন্বয়ের ডোমেন কোনটি?
ক) {2, 4, 5, 7}
খ) {2, 2, 10, 7}
গ) {2, 4, 10, 7}
ঘ) {2, 4, 7}
২. S = {(x, y) : x ∈ A, y ∈ A এবং y = : x2} এবং A = {-2,-1,0,1,2} নিচের কোনটি S অন্বয়ের সদস্য?
ক) ( 2,4)
খ) (- 2, 4 )
গ) (–1, 1 )
ঘ) ( 1, − 1 )
৩. যদি S = {(1, 4), (2, 1), (3, 0 ), ( 4, 1), (5, 4)} হয় তবে,
(i) S অন্বয়ের রেঞ্জ { 4, 1, 0}
(ii) S অন্বয়ের বিপরীত অন্বয়, S-1 = {(4, 1), (1, 2), (0, 3), (1, 4), ( 4, 5)}
(iii) S অন্বয়টি একটি ফাংশন
উপরের তথ্যের আলোকে নিচের কোনটি সঠিক?
ক) i ও ii
খ) ii ও iii
গ) i ও iii
ঘ) i, ii ও iii
৪. যদি F(x) = Vx -1 হয় তবে F (10) = কত?
ক) 9
খ) 3
গ) – 3
ঘ) V10
5. S = {(x, y) : x2 + y2 – 25 = 0 এবং x > 0} হলে,
(i) অন্বয়টি ফাংশন নয় ।
(ii) অন্বয়টির লেখচিত্র একটি অর্ধবৃত্ত।
(iii) অন্বয়টির লেখচিত্র : অক্ষের উপর অর্ধতলে থাকবে।
নিচের কোনটি সঠিক?
ক) i, ii
খ) i, iii
গ) ii, iii
ঘ) i, ii ও iii
6. F(x) = Vx − 1 = 2 হলে x এর মান কত?
ক) 5
খ) 24
গ) 25
ঘ) 26
7. F(x) = Vx − 1 ফাংশনটির ডোমেন নিচের কোনটি?
ক) ডোম F = {x ∈ R : x = 1}
খ) ডোম F = {x ∈ R : x > 1}
গ) ডোম F = {x ∈ R : x ≤ 1}
ঘ) ডোম F = {x ∈ R : x > 1}
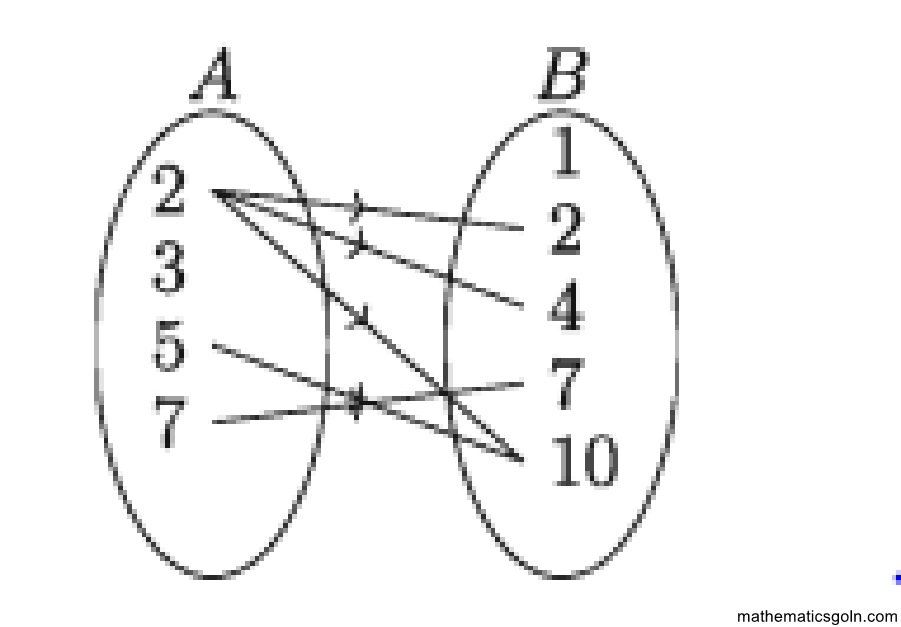
৮. (i) নিচে প্রদত্ত S অন্বয়গুলোর ডোমেন, রেঞ্জ ও বিপরীত অন্বয় নির্ণয় কর।
(ii) S অথবা S-1 অন্বয়গুলো ফাংশন কিনা তা নির্ধারণ কর।
(iii) ফাংশনগুলো এক-এক কিনা নির্ধারণ কর।
ক) S = { (1, 5), (2, 10 ), ( 3, 15 ), ( 4, 20) }
খ) S={(-3,8), (-2, 3), (-1, 0), (0, −1), (1, 0), (2, 3), (3,8)}
গ) 5 – {(2.0), (1.1), (1. -1), (2012). (-2)} st) S = ,2
ঘ) S = {(−3, −3), (−1, −1), (0, 0), (1, 1), (3, 3)}
ঙ) S = {(2, 1), (2, 2), (2, 3)}
৯. F(x) = Vx – 1 দ্বারা বর্ণিত ফাংশনের জন্য
ক) F (1), F(5) এবং F(10) নির্ণয় কর।
খ) F(a2 + 1) নির্ণয় কর যেখানে a ∈ R
গ) F(x) = 5 হলে, x নির্ণয় কর।
ঘ) F(x) = y হলে, নির্ণয় কর যেখানে y 201
১০. F : R → R, F(x) = x3 ফাংশনের জন্য
ক) ডোম F এবং রেঞ্জ F নির্ণয় কর।
খ) দেখাও যে, F এক-এক ফাংশন।
গ) F-1 নির্ণয় কর।
ঘ) দেখাও যে, F-1 একটি ফাংশন।
১১. ক) f : R → R একটি ফাংশন যা f(x) = ax + b; a, b ∈ R a≠0 দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f এক-এক এবং সার্বিক ।
খ) f : [0, 1] → [0, 1] ফাংশনটি f(x) = √1 – x2 দ্বারা সংজ্ঞায়িত হলে, দেখাও যে, f – এক-এক এবং সার্বিক।
১২. ক) যদি f : R → R এবং g : R → R ফাংশনদ্বয় f(x) = x +5 এবং g(x) = (x-5) 3 দ্বারা সংজ্ঞায়িত হয়, তবে দেখাও যে, g = f-11
খ) যদি f : R → R ফাংশনটি f(x) = 5x – 4 দ্বারা সংজ্ঞায়িত হয়, তবে, y = f−1(x) নির্ণয় কর।
১৩. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর।
ক) S = {(x, y) : 2x – y + 5 = 0}
খ) S = {(x, y) : x + y = 1}
গ) S {(x, y) : 3x + y = 4} =
ঘ) S = {(x, y) : x = -2}
১৪. S অন্বয়ের লেখচিত্র অঙ্কন কর এবং অন্বয়টি ফাংশন কিনা তা লেখচিত্র থেকে নির্ণয় কর।
ক) S = {(x, y) : x2 + y2 = 25}
খ) S = {(x, y) : x2 + y = 9}
১৫. দেওয়া আছে, F ( x ) = 2x – 1।
ক) F(x + 1) এবং F(1/2)এর মান নির্ণয় কর।
খ) F(x) ফাংশনটি এক-এক কিনা তা যাচাই কর, যখন X, Y ERI
গ) F(x) = y হলে x এর তিনটি পূর্ণ সাংখ্যিক মানের জন্য y এর মান নির্ণয় কর এবং y = 2x – 1 সমীকরণটির লেখচিত্র অঙ্কন কর।
১৬. f : R → R এবং g : R → R ফাংশন দুইটি যথাক্রমে f(x) = 3x+3 এবং g(x) = (x-3)/3 দ্বারা সংজ্ঞায়িত।
ক) g1 (−3) এর মান নির্ণয় কর।
খ) f(x) সার্বিক ফাংশন কিনা তা নির্ধারণ কর।
গ) দেখাও যে, g = f-1
১৭. দেওয়া আছে, f(x) = Vx – 4।
ক) f(x) এর ডোমেন নির্ণয় কর।
খ) f(x) এক-এক ফাংশন কিনা নির্ধারণ কর।
গ) f− 1 (x) ফাংশন কিনা তা লেখচিত্রের সাহায্যে নির্ণয় কর।
বিভিন্ন প্রকার সেট :
