আজকের আলোচনার বিষয়ঃ ত্রিভুজ অঙ্কনের যত পদ্ধতি । যা উচ্চতর গণিতের অন্তর্গত।
ত্রিভুজ অঙ্কনের যত পদ্ধতি
ত্রিভুজ হল এমন একটি বহুভুজ যার তিনটি বাহু এবং তিনটি শীর্ষবিন্দু রয়েছে। এটি জ্যামিতির মূল আকারগুলির মধ্যে একটি। A, B, এবং C শীর্ষবিন্দুসহ একটি ত্রিভুজকে △ABC দ্বারা প্রকাশ করা হয়।
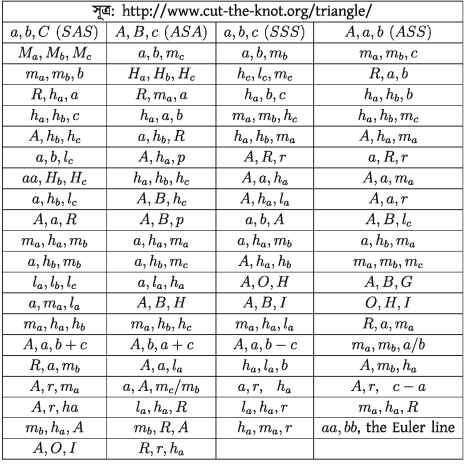
সাধারণভাবে একটি ত্রিভুজ দুইটি বাহু ও একটি কোণ (SAS), দুইটি কোণ ও অন্তর্ভুক্ত বাহু (ASA) অথবা তিনটি বাহু (SSs) দ্বারা নির্দিষ্ট। কিন্তু এছাড়াও নানাভাবে ত্রিভুজ অঙ্কন করা যেতে পারে। এই পদ্ধতিগুলো তালিকাভুক্ত করার পূর্বে নিম্নের প্রতীকগুলো সংজ্ঞায়িত করি।
|
A, B, C কোণ অথবা শীর্ষ বিন্দু |
ছেদবিন্দু |
| a, b, c যথাক্রমে A, B, C শীর্ষের বিপরীত বাহুর দৈর্ঘ্য | G : ভরকেন্দ্র |
| ha, ho, he: যথাক্রমে a, b, c বাহুর উপর বিপরীত শীর্ষ থেকে অঙ্কিত উচ্চতা | I, r: যথাক্রমে অন্তঃবৃত্তের কেন্দ্র ও ব্যাসার্ধ |
| ma, mb, mc: যথাক্রমে a, b, c বাহুর উপর অঙ্কিত মধ্যমা | Ia, Ib, Ic: AABC ত্রিভুজের যেকোনো দুইবাহু a b কে তাদের সাধারণ বিন্দুর বিপরীত দিকে বর্ধিত করলে যে রেখাদ্বয় তৈরি হয় তা এবং অন্য বাহু যে বৃত্তের স্পর্শক তার কেন্দ্রকে /, এবং ব্যাসার্ধকে ra বলে। Ta অন্যান্য প্রতীকগুলো অনুরূপভাবে সংজ্ঞায়িত |
| Lalon le: যথাক্রমে A, B, C কোণের সমদ্বিখণ্ডক | p: অর্ধপরিসীমা = (a+b+c) 2 |
| Ha, Hy, He: যথাক্রমে a, b, c বাহুর উপর বিপরীত শীর্ষ থেকে অঙ্কিত লম্বের পাদবিন্দু | aa, bb cc: যথাক্রমে a, b, c বাহুগুলোকে বর্ধিত করলে যে রেখাসমূহ হয় |
| Ma, Moy Me: যথাক্রমে বাহুগুলোর মধ্যবিন্দু | S: ত্রিভুজের ক্ষেত্রফল |
| La, Lb, Le: যথাক্রমে a, b, c বাহুর উপর বিপরীত শীর্ষ কোণের সমদ্বিখণ্ডকের পাদবিন্দু |
Sa, So, Se যথাক্রমে A, B, C কোণের সমদ্বিখণ্ডকের সাপেক্ষে ওই বিন্দুসমূহ থেকে অঙ্কিত মধ্যমাগুলোর প্রতিসম সরলরেখাসমূহের পাদবিন্দু। |
| O, R: পরিকেন্দ্র ও পরিবৃত্তের ব্যাসার্ধ | |
| H : শীর্ষবিন্দু থেকে অঙ্কিত উচ্চতাসমূহের |