দশমিক ভগ্নাংশ

আজকে আমাদের আলোচনার বিষয়ঃ দশমিক ভগ্নাংশ । এটি নবম – দশম শ্রেনী গণিতের বাস্তব সংখ্যার অন্তর্গত।

 

 

দশমিক ভগ্নাংশ (Decimal Fractions )

প্রত্যেক বাস্তব সংখ্যাকে দশমিক ভগ্নাংশে প্রকাশ করা যায়। যেমন 2 = 2.0, 2/5 = 0.4, 1/3 = 0.333 … ইত্যাদি। দশমিক ভগ্নাংশ তিন প্রকার: সসীম, আবৃত্ত এবং অসীম দশমিক ভগ্নাংশ।

সসীম দশমিক ভগ্নাংশ:

কোনো সসীম দশমিক ভগ্নাংশে দশমিক বিন্দুর ডানদিকে সসীম সংখ্যক অঙ্ক থাকে। যেমন 0.12, 1.023 7.832, 54.67, . ইত্যাদি সসীম দশমিক ভগ্নাংশ।

আবৃত্ত দশমিক ভগ্নাংশ:

কোনো আবৃত্ত দশমিক ভগ্নাংশে দশমিক বিন্দুর ডানদিকের অঙ্কগুলোর সব অথবা পরপর থাকা কিছু অংশ বারবার আসতে থাকে। যেমন, 3.333, 2.454545… – 5.12765765… ইত্যাদি আবৃত্ত দশ-মিক ভগ্নাংশ ।

অসীম দশমিক ভগ্নাংশ:

কোনো অসীম দশ-মিক ভগ্নাংশে দশমিক বিন্দুর ডানদিকের অঙ্ক কখনো শেষ হয় না, অর্থাৎ দশমিক বিন্দুর ডানদিকের অঙ্কগুলো সসীম হবে না এবং অংশবিশেষ বারবার আসবে না। যেমন √2 = 1.4142135624… V7 = 2.6457513111 … ইত্যাদি অসীম দশ-মিক ভগ্নাংশ।

মন্তব্য:

সসীম দশমিক ও আবৃত্ত দশ-মিক ভগ্নাংশ হলো মূলদ সংখ্যা এবং অসীম দশ-মিক ভগ্নাংশ হলো অমূলদ সংখ্যা। কোনো অমূলদ সংখ্যার মান যত দশমিক স্থান পর্যন্ত ইচ্ছা নির্ণয় করা যায়। কোনো ভগ্নাংশের লব ও হরকে স্বাভাবিক সংখ্যায় প্রকাশ করতে পারলে, ঐ ভগ্নাংশটি মূলদ সংখ্যা।

আবৃত্ত দশমিক ভগ্নাংশ

 

 

23/ 6 সাধারণ ভগ্নাংশটিকে দশমিক ভগ্নাংশে প্ৰকাশ করি। লক্ষ করি, ভগ্নাংশের লবকে হর দিয়ে ভাগ করে দশ-মিক ভগ্নাংশে পরিণত করার সময় ভাগের প্রক্রিয়া শেষ হয় নাই। দেখা যায় যে, ভাগফলে একই অঙ্ক ও বারবার আসে। এখানে 3.8333… একটি আবৃত্ত দশমিক ভগ্নাংশ।

যে সকল দশমিক ভগ্নাংশে দশমিক বিন্দুর ডানে একটি অঙ্ক বারবার আসে বা একাধিক অঙ্ক পর্যায়ক্রমে বারবার আসে, এদের আবৃত্ত দশ-মিক ভগ্নাংশ বলা হয়। আবৃত্ত বা পৌনঃপুনিক দশ-মিক ভগ্নাংশে যে অংশ বারবার অর্থাৎ পুনঃপুন আসে, একে আবৃত্ত অংশ আর বাকি অংশকে অনাবৃত্ত অংশ বলা হয়।

আবৃত্ত দশ-মিক ভগ্নাংশে একটি অঙ্ক আবৃত্ত হলে, সে অঙ্কের উপর পৌনঃপুনিক বিন্দু এবং একাধিক অঙ্ক আবৃত্ত হলে, কেবলমাত্র প্রথম ও শেষ অঙ্কের উপর পৌনঃপুনিক বিন্দু দেওয়া হয়। যেমন, 2.555 … কে লেখা হয় 2.5 দ্বারা এবং 3.124124124 … কে লেখা হয়, 3.124 দ্বারা।

দশ-মিক ভগ্নাংশে দশমিক বিন্দুর পর আবৃত্তাংশ ছাড়া অন্য কোনো অঙ্ক না থাকলে, একে বিশুদ্ধ পৌনঃপুনিক ভগ্নাংশ বলা হয় এবং পৌনঃপুনিক দশ-মিক ভগ্নাংশে দশমিক বিন্দুর পর আবৃত্তাংশ ছাড়া এক বা একাধিক অঙ্ক থাকলে, একে মিশ্র পৌনঃপুনিক ভগ্নাংশ বলা হয়। যেমন, 1.3 বিশুদ্ধ পৌনঃপুনিক ভগ্নাংশ এবং 4.235112 মিশ্র পৌনঃপুনিক ভগ্নাংশ ।

ভগ্নাংশের হরে 2, 5 ছাড়া অন্য কোনো মৌলিক গুণনীয়ক (উৎপাদক) থাকলে, সেই হর দ্বারা লবকে ভাগ করলে, কখনো নিঃশেষে বিভাজ্য হবে না। যেহেতু পর্যায়ক্রমে ভাগ শেষে 1, 2, 9 ছাড়া অন্য কিছু হতে পারে না, সেহেতু এক পর্যায়ে ভাগশেষগুলো বারবার একই সংখ্যা হতে থাকবে। আবৃত্তাংশের অঙ্ক সংখ্যা সবসময় হরে যে সংখ্যা থাকে, এর চেয়ে ছোট হয়।

 

 

আবৃত্ত দশমিক ভগ্নাংশকে সাধারণ ভগ্নাংশে পরিবর্তন

উদাহরণ 8.

0.3, 0.24, এবং 42.3478 কে সাধারণ ভগ্নাংশে প্রকাশ কর।

সমাধান:

নিচে 0.3, 0.24, এবং 42.3478 কে সাধারণ ভগ্নাংশে পরিণত করা হয়েছে।

 

 

ব্যাখ্যা:

উপরের তিনটি উদাহরণ থেকে দেখা যায় যে,

• আবৃত্ত দশমিক ভগ্নাংশে দশমিক বিন্দুর পর যে কয়টি অঙ্ক আছে, সে কয়টি শূন্য 1 এর ডানে বসিয়ে প্রথমে আবৃত্ত দশমিক ভগ্নাংশকে গুণ করা হয়েছে।
• আবৃত্ত দশমিক ভগ্নাংশে দশমিক বিন্দুর পর যে কয়টি অনাবৃত্ত অঙ্ক আছে, সে কয়টি শূন্য 1 এর ডানে বসিয়ে আবৃত্ত দশমিক ভগ্নাংশকে গুণ করা হয়েছে।
•  প্রথম গুণফল থেকে দ্বিতীয় গুণফল বিয়োগ করা হয়েছে এবং তাতে ডানপক্ষে পূর্ণসংখ্যা পাওয়া গেছে। এখানে লক্ষণীয় যে, আবৃত্ত দশমিক ভগ্নাংশের দশমিক ও পৌনঃপুনিক বিন্দু উঠিয়ে প্রাপ্ত সংখ্যা থেকে অনাবৃত্ত অংশের সংখ্যা বিয়োগ করা হয়েছে।
• আবৃত্ত দশমিক ভগ্নাংশে যতগুলো আবৃত্ত অঙ্ক ছিল ততগুলো 9 লিখে এবং তাদের ডানে দশমিক বিন্দুর পর যতগুলো অনাবৃত্ত অঙ্ক ছিল ততগুলো শূন্য বসিয়ে উপরে প্রাপ্ত বিয়োগফলকে ভাগ করা হয়েছে।
• আবৃত্ত দশমিক ভগ্নাংশকে সাধারণ ভগ্নাংশে পরিণত করায় সাধারণ ভগ্নাংশটির হর হলো যতগুলো আবৃত্ত অঙ্ক ততগুলো 9 এবং 9 গুলোর ডানে দশমিক বিন্দুর পর যতগুলো অনাবৃত্ত অঙ্ক ততগুলো শূন্য। আর সাধারণ ভগ্নাংশটির লব হলো আবৃত্ত দশমিক ভগ্নাংশের দশমিক বিন্দু ও পৌনঃপুনিক বিন্দু উঠিয়ে যে সংখ্যা পাওয়া গেছে, সে সংখ্যা থেকে আবৃত্তাংশ বাদ দিয়ে বাকি অঙ্ক দ্বারা গঠিত সংখ্যা বিয়োগ করে পাওয়া বিয়োগফল।

মন্তব্য:

আবৃত্ত দশমিক ভগ্নাংশকে সব সময় সাধারণ ভগ্নাংশে পরিণত করা যায়। সকল আবৃত্ত দশমিক ভগ্নাংশ মূলদ সংখ্যা ।

 

 

ব্যাখ্যা:

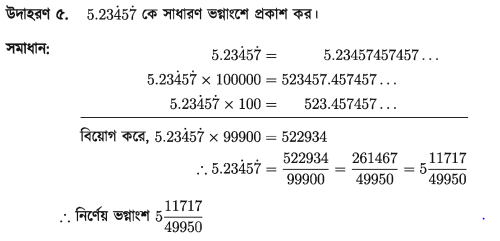
দশমিক অংশে পাঁচটি অঙ্ক রয়েছে বলে এখানে আবৃত্ত দশ-মিক ভগ্নাংশকে প্রথমে 100000 (এক এর ডানে পাঁচটি শূন্য) দ্বারা গুণ করা হয়েছে। আবৃত্ত অংশের বামে দশমিক অংশে দুইটি অঙ্ক রয়েছে বলে আবৃত্ত দশমিক ভগ্নাংশকে 100 (এক এর ডানে দুইটি শূন্য) দ্বারা গুণ করা হয়েছে। প্রথম গুণফল থেকে দ্বিতীয় গুণফল বিয়োগ করা হয়েছে। এই বিয়োগফলের একদিকে পূর্ণসংখ্যা অন্যদিকে প্রদত্ত আবৃত্ত দশমিক ভগ্নাংশের মানের ( 100000 – 1000 ) = 99900 গুণ। উভয় পক্ষকে 99900 দিয়ে ভাগ করে নির্ণেয় সাধারণ ভগ্নাংশ পাওয়া গেল।

আবৃত্ত দশমিক ভগ্নাংশকে সাধারণ ভগ্নাংশে রূপান্তরের নিয়ম:

নির্ণেয় ভগ্নাংশের লব = প্রদত্ত দশমিক ভগ্নাংশের দশমিক বিন্দু বাদ দিয়ে প্রাপ্ত পূর্ণসংখ্যা এবং অনাবৃত্ত অংশ দ্বারা গঠিত পূর্ণসংখ্যার বিয়োগফল।

নির্ণেয় ভগ্নাংশের হর = দশমিক বিন্দুর পরে আবৃত্ত অংশে যতগুলো অঙ্ক আছে ততগুলো নয় (9) এবং অনাবৃত্ত অংশে যতগুলো অঙ্ক আছে ততগুলো শূন্য (0) দ্বারা গঠিত সংখ্যা ।

নিচের উদাহরণগুলোতে এ নিয়ম সরাসরি প্রয়োগ করে কয়েকটি আবৃত্ত দশমিককে সাধারণ ভগ্নাংশে পরিণত করা হলো।

উদাহরণ ৬.

45.2346 কে সাধারণ ভগ্নাংশে প্রকাশ কর।

সমাধান:

45.2346 = (452346-452)/9990 = 451894/9990 = 225947/4995 = 45(1172/4995)

.:. নির্ণেয় ভগ্নাংশ 45(1172/4995)

উদাহরণ ৭.

32.567 কে সাধারণ ভগ্নাংশে প্রকাশ কর।

সমাধান:

32.567 = (32567 – 32)/999 = 32535/999 =3615/111 = 1205/37 = 32(21/37)

নির্ণেয় ভগ্নাংশ 32(21/37)

 

সদৃশ আবৃত্ত দশমিক ও অসদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ

দুই বা ততোধিক আবৃত্ত দশ-মিক ভগ্নাংশের অনাবৃত্ত ও আবৃত্ত উভয় অংশের অঙ্ক সংখ্যা সমান হলে এদের সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ বলে। অন্যথায় এদেরকে অসদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ বলে। যেমন 12.45 ও 6.32; 9.453 ও 125.897 সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ। আবার, 0.3456 ও 7.45789; 6.4357 ও 2.89345 অসদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ ।

অসদৃশ আবৃত্ত দশ-মিক ভগ্নাংশগুলোকে সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশে পরিবর্তন

কোনো আবৃত্ত দশ-মিক ভগ্নাংশের আবৃত্ত অংশের অঙ্কগুলোকে বারবার লিখলে দশ-মিক ভগ্নাংশের মানের কোনো পরিবর্তন হয় না। যেমন 6.4537 = 6.453737 = 6.45373 = 6.453737। এখানে প্রত্যেকটিই একই আবৃত্ত দশ-মিক ভগ্নাংশ 6.45373737, যেটি একটি অসীম দশমিক সংখ্যা। এই আবৃত্ত দশ-মিক ভগ্নাংশগুলোকে সাধারণ ভগ্নাংশে পরিবর্তন করলে দেখা যাবে প্রত্যেকটি সমান।

 

 

সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশে পরিণত করতে হলে ভগ্নাংশগুলোর মধ্যে যে ভগ্নাংশটির অনাবৃত্ত অংশের অঙ্ক সংখ্যা বেশি, প্রত্যেকটি ভগ্নাংশের অনাবৃত্ত অংশের অঙ্ক সংখ্যাকে ওই ভগ্নাংশটির অনাবৃত্ত অংশের অঙ্কের সংখ্যার সমান করতে হবে এবং বিভিন্ন সংখ্যায় আবৃত্ত অংশের অঙ্ক সংখ্যাগুলোর ল.সা.গু. যত, প্রত্যেকটি দশ-মিক ভগ্নাংশের আবৃত্ত অংশ তত অঙ্কের করতে হবে।

উদাহরণ ৮.

5.6, 7.345 ও 1078423 কে সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশে পরিণত কর।

সমাধান:

5.6, 7.345, ও 10.78423 আবৃত্ত দশ-মিক ভগ্নাংশে অনাবৃত্ত অংশের অঙ্ক সংখ্যা যথাক্রমে 0, 1 ও 2। এখানে 10.78423 এর অনাবৃত্ত অঙ্ক সংখ্যা দশমিকে সবচেয়ে বেশি এবং এ সংখ্যা 2 তাই সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ করতে হলে প্রত্যেকটি দশমিক ভগ্নাংশের অনাবৃত্ত অংশের অঙ্ক সংখ্যা 2 করতে হবে। 5.6, 7.345 ও 1078423 আবৃত্ত দশ-মিক ভগ্নাংশে আবৃত্ত অংশের অঙ্ক সংখ্যা যথাক্রমে 1, 2 ও 3। 1, 2 ও 3 এর ল.সা.গু হলো 6। তাই সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশ করতে হলে প্রত্যেকটি দশ-মিক ভগ্নাংশের আবৃত্ত অংশের অঙ্ক সংখ্যা 6 করতে হবে। সুতরাং 5.6 = 5.66666666, 7.345 = 7.34545454 31078423 = 1078423423। নির্ণেয় সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশসমূহ যথাক্রমে 5.66666666, 7.34545454 ও 10.784 23423

উদাহরণ ৯.

1.7643, 3.24, ও 2.78346 কে সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশে পরিণত কর।

সমাধান:

1.7643 এ অনাবৃত্ত অংশ বলতে দশমিক বিন্দুর পরের 4টি অঙ্ক, এখানে আবৃত্ত অংশ নেই । 3.24 এ অনাবৃত্ত অংশের অঙ্ক সংখ্যা 0 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 2, 2.78346 এ অনাবৃত্ত অংশের অঙ্ক সংখ্যা 2 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 3। এখানে অনাবৃত্ত অংশের অঙ্ক সংখ্যা সবচেয়ে বেশি হলো 4 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 2 ও 3 এর ল.সা.গু. হলো 6। প্রত্যেকটি দশ-মিক ভগ্নাংশের অনাবৃত্ত অংশের অঙ্ক সংখ্যা হবে 4 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা হবে 61 … 1.7643 1.7643000000, 3.243.24242424242.78346 = 2.7834634634 = নির্ণেয় সদৃশ আবৃত্ত দশ-মিক ভগ্নাংশসমূহ 1.7643000000, 3.2424242424 ও 2.7834634634

মন্তব্য:

সসীম দশ-মিক ভগ্নাংশগুলোকে সদৃশ দশ-মিক ভগ্নাংশে পরিণত করার জন্য দশমিক বিন্দুর সর্বডানের অঙ্কের পর প্রয়োজনীয় সংখ্যক শূন্য বসিয়ে প্রত্যেকটি দশ-মিক ভগ্নাংশের দশমিক বিন্দুর পরের অনাবৃত্ত অঙ্ক সংখ্যা সমান করা হয়েছে। আর আবৃত্ত দশমিক ভগ্নাংশের ক্ষেত্রে প্রত্যেকটি দশ-মিক ভগ্নাংশে দশমিক বিন্দুর পরের অনাবৃত অঙ্ক সংখ্যা সমান এবং আবৃত্ত অঙ্ক সংখ্যা সমান করা হয়েছে আবৃত্ত অঙ্কগুলো ব্যবহার করে। অনাবৃত্ত অংশের পর যে কোনো অঙ্ক থেকে শুরু করে আবৃত্ত অংশ নেওয়া যায়।