বৃত্তচাপ জ্যামিতি

আজকে আমাদের  আলোচনার বিষয়ঃ বৃত্তচাপ জ্যামিতি। এটি নবম – দশম শ্রেনী গণিতের বৃত্ত এর অন্তর্গত।

 

 

বৃত্তচাপ জ্যামিতি

বৃত্তের যেকোনো দুইটি বিন্দুর মধ্যের পরিধির অংশকে বৃত্তচাপ বলে। চিত্রে A ও B দুইটি বিন্দুর মাঝে বৃত্তের অংশগুলো লক্ষ করি। দেখা যায়, দুইটি অংশের একটি অংশ ছোট, অন্যটি তুলনামূলকভাবে বড়। ছোট অংশটিকে উপচাপ ও বড়টিকে অধিচাপ বলা হয়। A ও B এই চাপের প্রান্তবিন্দু এবং চাপের অন্য সকল বিন্দু তার অন্তঃস্থ বিন্দু। চাপের অন্তঃস্থ একটি বিন্দু R নির্দিষ্ট করে চাপটিকে ARB চাপ বলে অভিহিত করা হয় এবং ARB প্রতীক দ্বারা প্রকাশ করা হয়। আবার কখনো উপচাপটি AB প্রতীক দ্বারা প্রকাশ করা হয়। বৃত্তের দুইটি বিন্দু A ও B বৃত্তটিকে দুইটি চাপে বিভক্ত করে। উভয় চাপের প্রান্তবিন্দু A ও B এবং প্রান্তবিন্দু ছাড়া চাপ দুইটির অন্য কোনো সাধারণ বিন্দু নেই।

 

 

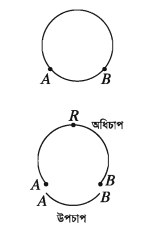
কোণ কর্তৃক খণ্ডিত চাপ

একটি কোণ কোনো বৃত্তে একটি চাপ খণ্ডিত বা ছিন্ন করে বলা হয় যদি

১. চাপটির প্রত্যেক প্রান্তবিন্দু কোণটির বাহুতে অবস্থিত হয়,

২. কোণটির প্রত্যেক বাহুতে চাপটির অন্তত একটি প্রান্তবিন্দু অবস্থিত হয় এবং

৩. চাপটির অন্তঃস্থ প্রত্যেকটি বিন্দু কোণটির অভ্যন্তরে থাকে। চিত্রে প্রদর্শিত কোণটি O কেন্দ্রিক বৃত্তে APB চাপ খণ্ডিত করে।

 

 

বৃত্তস্থ কোণ (Inscribed angle )

বৃত্তের দুইটি জ্যা পরস্পরকে বৃত্তের উপর কোনো বিন্দুতে ছেদ করলে এদের মধ্যবর্তী কোণকে বৃত্তস্থ কোণ বা বৃত্তে অন্তর্লিখিত কোণ বলা হয়। চিত্রে ZACB বৃত্তস্থ কোণ। প্রত্যেক বৃত্তস্থ কোণ বৃত্তে একটি চাপ খণ্ডিত করে। এই চাপ উপচাপ, অর্ধবৃত্ত অথবা অধিচাপ হতে পারে।

একটি বৃত্তস্থ কোণ বৃত্তে যে চাপ খণ্ডিত করে, কোণটি সেই চাপের ওপর দণ্ডায়মান এবং খণ্ডিত চাপের অনুবন্ধী চাপে অন্তর্লিখিত বলা হয়।

পাশের চিত্রে বৃত্তস্থ কোণটি APB চাপের ওপর দণ্ডায়মান এবং ACB চাপে অন্তর্লিখিত।

লক্ষণীয় যে, APB ও ACB একে অপরের অনুবন্ধী চাপ।

 

 

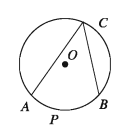
মন্তব্য:

বৃত্তের কোনো চাপে অন্তর্লিখিত একটি কোণ হচ্ছে সেই কোণ যার শীর্ষবিন্দু ঐ চাপের একটি অন্তঃস্থ বিন্দু এবং যার এক একটি বাহু ঐ চাপের এক একটি প্রান্তবিন্দু দিয়ে যায়। বৃত্তের কোনো চাপে দণ্ডায়মান একটি বৃত্তস্থ কোণ হচ্ছে ঐ চাপের অনুবন্ধী চাপে অন্তর্লিখিত একটি কোণ।

কেন্দ্রস্থ কোণ (Central angle )

একটি কোণের শীর্ষবিন্দু কোনো বৃত্তের কেন্দ্রে অবস্থিত হলে, কোণটিকে ঐ বৃত্তের একটি কেন্দ্রস্থ কোণ বলা হয় এবং কোণটি বৃত্তে যে চাপ খণ্ডিত করে সেই চাপের ওপর তা দণ্ডায়মান বলা হয়। পাশের চিত্রের ∠AOB কোণটি একটি কেন্দ্রস্থ কোণ এবং তা APB চাপের ওপর দণ্ডায়মান। প্রত্যেক কেন্দ্রস্থ কোণ বৃত্তে একটি উপচাপ খণ্ডিত করে। চিত্রে APB একটি উপচাপ। বৃত্তের কোনো উপচাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বলতে এরূপ কোণকেই বোঝায় যার শীর্ষবিন্দু বৃত্তের কেন্দ্রে অবস্থিত এবং যার বাহুদ্বয় ঐ চাপের প্রান্তবিন্দু দুইটি দিয়ে যায়।

অর্ধবৃত্তের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বিবেচনার জন্য ওপরে উল্লেখিত বর্ণনা অর্থবহ নয়। অর্ধবৃত্তের ক্ষেত্রে কেন্দ্রস্থ কোণ ∠BOC সরলকোণ এবং বৃত্তস্থ কোণ ∠BAC সমকোণ।

 

 

উপপাদ্য ২০.

বৃত্তের একই চাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ।

মনে করি, O কেন্দ্রবিশিষ্ট ABC একটি বৃত্ত এবং তার একই উপচাপ BC এর ওপর দণ্ডায়মান ∠BAC বৃত্তস্থ এবং ∠BOC কেন্দ্ৰস্থ কোণ।

প্রমাণ করতে হবে যে, ∠BOC = 2∠BAC

অঙ্কন :

মনে করি, AC রেখাংশ কেন্দ্রগামী নয়। এ ক্ষেত্রে A বিন্দু দিয়ে কেন্দ্রগামী রেখাংশ AD আঁকি।

 

 

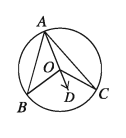
প্ৰমাণ:

ধাপ ১.

∆AOB এর বহিঃস্থ কোণ ∠BOD ∠BAO + ∠ABO = [: বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]

ধাপ ২.

∆AOB এ OA = OB   [:: একই বৃত্তের ব্যাসার্ধ ]

ধাপ ৩.

ধাপ (১) ও (২) থেকে ∠BOD = 2∠BAO

ধাপ ৪.

একইভাবে ∆AOC থেকে ∠COD = 2∠CAO

ধাপ ৫.

ধাপ (৩) ও (৪) থেকে

∠BOD+∠COD=2∠BAO+2∠CAO [যোগ করে]

অর্থাৎ ∠BOC = 2∠BAC। (প্রমাণিত)

অন্যভাবে বলা যায়, বৃত্তের একই চাপের ওপর দণ্ডায়মান বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক।

উপপাদ্য ২১.

বৃত্তের একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণগুলো পরস্পর সমান।

মনে করি, O বৃত্তের কেন্দ্র এবং বৃত্তের BCD চাপের ওপর দণ্ডায়মান ∠BAD এবং ∠BED দুইটি বৃত্তস্থ কোণ।

প্রমাণ করতে হবে যে, ∠BAD = ∠BED

অঙ্কন :

O, B এবং O, D যোগ করি।

 

 

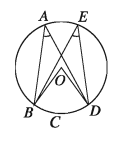
প্ৰমাণ:

ধাপ ১.

এখানে BCD চাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ ∠BOD

সুতরাং, ∠BOD = 2∠BAD এবং ∠BOD = 2∠BED

[‘.’ একই চাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ ]

2∠BAD=2∠BED

বা ∠BAD = ∠BED। (প্রমাণিত)

উপপাদ্য ২২.

অর্ধবৃত্তস্থ কোণ এক সমকোণ ।

মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস এবং ∠ACB একটি অর্ধবৃত্তস্থ কোণ। প্রমাণ করতে হবে যে, ∠ACB এক সমকোণ।

অঙ্কন :

AB এর যে পাশে C বিন্দু অবস্থিত, তার বিপরীত পাশে বৃত্তের উপর একটি বিন্দু D নিই।

 

 

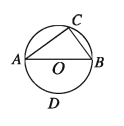
প্ৰমাণ:

ধাপ ১.

ADB চাপের ওপর দণ্ডায়মান

বৃত্তস্থ ∠ACB = 1/2(কেন্দ্রস্থ সরল কোণ ∠AOB ) = [:: একই চাপের ওপর দণ্ডায়মান বৃত্তস্থ কোণ কেন্দ্ৰস্থ কোণের অর্ধেক ]

ধাপ ২.

কিন্তু সরলকোণ ∠AOB = দুই সমকোণ।

∠ACB =  1/2 (দুই সমকোণ) = এক সমকোণ। (প্রমাণিত)

অনুসিদ্ধান্ত ৪

সমকোণী ত্রিভুজের অতিভুজকে ব্যাস ধরে বৃত্ত অঙ্কন করলে তা সমকৌণিক শীর্ষবিন্দু দিয়ে যাবে।

অনুসিদ্ধান্ত ৫.

কোনো বৃত্তের অধিচাপে অন্তর্লিখিত কোণ সূক্ষ্মকোণ

অনুশীলনী

১. O কেন্দ্রবিশিষ্ট কোনো বৃত্তে ABCD একটি অন্তর্লিখিত চতুর্ভুজ। AC, BD কর্ণদ্বয় E বিন্দুতে ছেদ করলে প্রমাণ কর যে, ∠AOB + ∠COD = 2∠AEB

২. ০ কেন্দ্রবিশিষ্ট বৃত্তে ABCD একটি অন্তর্লিখিত চতুর্ভুজ। ∠ADB + ∠BDC  = এক সমকোণ। প্রমাণ কর যে, A, O, C এক সরলরেখায় অবস্থিত।

৩. দেখাও যে, বৃত্তস্থ ট্রাপিজিয়ামের তির্যক বাহুদ্বয় পরস্পর সমান।

৪. চিত্রে, O বৃত্তের কেন্দ্র এবং OB = 2.5 সে.মি.

ক) ABCD বৃত্তটির পরিধি নির্ণয় কর।

খ) প্রমাণ কর যে, ∠BAD = ∠BOD

গ) AC ও BD পরস্পর E বিন্দুতে ছেদ করলে

প্রমাণ কর যে, ∠AOB + ∠COD = 2∠AEB

 

 

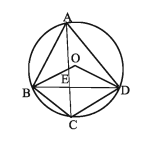
৫. ABCD বৃত্তে AB ও CD জ্যা দুইটি পরস্পর দ্র বিন্দুতে ছেদ করেছে। দেখাও যে, ∆AED ও ∆BEC সদৃশকোণী।