আজকে আমাদের আলোচনার বিষয়ঃ বৃত্তস্থ চতুর্ভুজ । এটি নবম – দশম শ্রেনী গণিতের বৃত্ত এর অন্তর্গত।

বৃত্তস্থ চতুর্ভুজ (Inscribed Quadrilaterals)
বৃত্তীয় চতুর্ভুজ বা বৃত্তে অন্তর্লিখিত চতুর্ভুজ হলো এমন চতুর্ভুজ যার চারটি শীর্ষবিন্দু বৃত্তের উপর অবস্থিত। এ সকল চতুর্ভুজের বিশেষ কিছু ধর্ম রয়েছে। বিষয়টি অনুধাবনের জন্য নিচের কাজটি করি।
উপপাদ্য ২৩.
বৃত্তে অন্তর্লিখিত চতুর্ভুজের যেকোনো দুইটি বিপরীত কোণের সমষ্টি দুই সমকোণ।
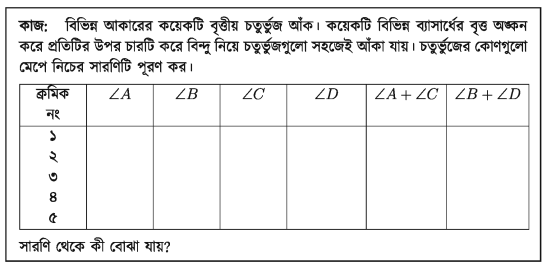
মনে করি, O কেন্দ্রবিশিষ্ট একটি বৃত্তে ABCD চতুর্ভুজটি অন্তর্লিখিত হয়েছে।
প্রমাণ করতে হবে যে, ∠ABC + ∠ADC = দুই সমকোণ এবং ∠BAD + ∠BCD = দুই সমকোণ।
অঙ্কন :
O, A এবং O,C যোগ করি।
প্ৰমাণ:
ধাপ ১.
একই চাপ ADC এর উপর দণ্ডায়মান কেন্দ্রস্থ প্রবৃদ্ধ ∠AOC = 2 (বৃত্তস্থ ∠ABC) অর্থাৎ, প্রবৃদ্ধ ∠AOC = 2∠ABC [বৃত্তের একই চাপের ওপর দণ্ডায়মান কেন্দ্ৰস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ]
ধাপ ২.
আবার, একই চাপ ABC এর উপর দণ্ডায়মান কেন্দ্রস্থ কোণ ∠AOC = 2 ( বৃত্তস্থ ∠ADC)
অর্থাৎ কোণ ∠AOC = 2∠ADC [বৃত্তের একই চাপের ওপর দণ্ডায়মান কেন্দ্ৰস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ]
প্রবৃদ্ধ ∠AOC+কোণ ∠AOC = 2 ( ∠ABC + ∠ADC)
কিন্তু প্রবৃদ্ধ ∠AOC+ কোণ ∠AOC = চার সমকোণ
2 ( ABC + LADC) = চার সমকোণ
∠ABC + ∠ADC = দুই সমকোণ।
একইভাবে, প্রমাণ করা যায় যে, ∠BAD + ∠BCD = দুই সমকোণ। (প্রমাণিত)
অনুসিদ্ধান্ত ৬
বৃত্তে অন্তর্লিখিত চতুর্ভুজের একটি বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা বিপরীত অন্তঃস্থ কোণের সমান।
অনুসিদ্ধান্ত ৭.
বৃত্তে অন্তর্লিখিত সামান্তরিক একটি আয়তক্ষেত্র।
উপপাদ্য ২৪.
কোনো চতুর্ভুজের দুইটি বিপরীত কোণ সম্পূরক হলে তার শীর্ষবিন্দু চারটি সমবৃত্ত হয়।
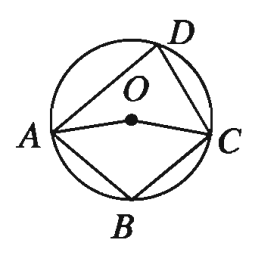
মনে করি, ABCD চতুর্ভুজে ∠ABC + ∠ADC দুই = সমকোণ। প্রমাণ করতে হবে যে, A, B, C, D বিন্দু চারটি সমবৃত্ত।
অঙ্কন:
যেহেতু A, B, C বিন্দু তিনটি সমরেখ নয়, সুতরাং বিন্দু তিনটি দিয়ে যায় এরূপ একটি ও কেবল একটি বৃত্ত আছে। মনে করি, বৃত্তটি AD রেখাংশকে E বিন্দুতে ছেদ করে। C, E যোগ করি।
প্রমাণ:
অঙ্কন অনুসারে ABCE বৃত্তস্থ চতুর্ভুজ।
সুতরাং ∠ABC + ∠AEC দুই সমকোণ [বৃত্তে অন্তর্লিখিত চতুর্ভুজের যেকোনো দুইটি বিপরীত = কোণের সমষ্টি দুই সমকোণ]
কিন্তু ∠ABC + ∠ADC = দুই সমকোণ [দেওয়া আছে]
∠AEC = ∠ADC
কিন্তু তা অসম্ভব। কারণ চিত্রে ACED এর বহিঃস্থ ∠AEC > বিপরীত অন্তঃস্থ ∠ADC
সুতরাং E এবং D বিন্দুদ্বয় ভিন্ন হতে পারে না। E বিন্দু অবশ্যই D বিন্দুর সাথে মিলে যাবে।
অতএব, A, B, C, D বিন্দু চারটি সমবৃত্ত। (প্রমাণিত)
অনুশীলনী
১. ∆ABC এ ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় P বিন্দুতে এবং বহির্দ্বিখণ্ডকদ্বয় Q বিন্দুতে মিলিত হলে, প্রমাণ কর যে, B, P, C, Q বিন্দু চারটি সমবৃত্ত।
২. ABCD একটি বৃত্ত। ∠CAB ও ∠CBA এর সমদ্বিখণ্ডক দুইটি P বিন্দুতে এবং ∠DBA ও ∠DAB কোণদ্বয়ের সমদ্বিখণ্ডক দুইটি Q বিন্দুতে মিলিত হলে, প্রমাণ কর যে, A, Q, P, B বিন্দু চারটি সমবৃত্ত।
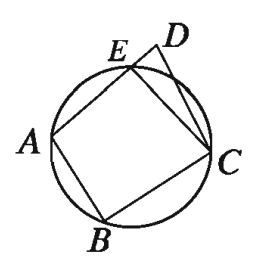
৩. O কেন্দ্রবিশিষ্ট বৃত্তের AB ও CD জ্যা দুইটি বৃত্তের অভ্যন্তরে অবস্থিত কোনো বিন্দুতে সমকোণে মিলিত হয়েছে। প্রমাণ কর যে, ∠AOD + ∠BOC = দুই সমকোণ।
৪. ABCD চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক। AC রেখা যদি ∠BAD এর সমদ্বিখণ্ডক হয়, তবে প্রমাণ কর যে, BC = CD
৫. O কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ 2.5 সে.মি., AB = 3 সে.মি. এবং BD, ∠ADC এর সমদ্বিখণ্ডক।
ক) AD এর দৈর্ঘ্য নির্ণয় কর।
খ) দেখাও যে, ∠ADC + ∠ABC = 180° ।
গ) প্রমাণ কর যে, AB = BC
৬. সমান সমান ভূমির ওপর অবস্থিত যেকোনো দুইটি ত্রিভুজের শিরঃকোণদ্বয় সম্পূরক হলে, প্রমাণ কর যে, এদের পরিবৃত্তদ্বয় সমান হবে।
৭. প্রমাণ কর যে, বৃত্তস্থ চতুর্ভুজের যেকোনো কোণের সমদ্বিখণ্ডক ও তার বিপরীত কোণের বহির্দ্বিখণ্ডক বৃত্তের ওপর ছেদ করে।
