আজকে আমাদের আলোচনার বিষয়ঃ সমকোণী ত্রিভুজের বাহুগুলোর নামকরণ । এটি নবম – দশম শ্রেনী গণিতের ত্রিকোণমিতিক অনুপাত এর অন্তর্গত।

ত্রিকোণমিতিক অনুপাত
সমকোণী ত্রিভুজের বাহুগুলোর নামকরণ
আমরা জানি, সমকোণী ত্রিভুজের বাহুগুলো অতিভুজ, ভূমি ও উন্নতি নামে অভিহিত হয়। ত্রিভুজের অনুভূমিক অবস্থানের জন্য এ নামসমূহ সার্থক। আবার সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটির সাপেক্ষে অবস্থানের প্রেক্ষিতেও বাহুগুলোর নামকরণ করা হয়। যথা:
১. ‘অতিভুজ (hypotenuse)’, সমকোণী ত্রিভুজের বৃহত্তম বাহু যা সমকোণের বিপরীত বাহু
২ . ‘বিপরীত বাহু (opposite side)’, যা হলো প্রদত্ত কোণের সরাসরি বিপরীত দিকের বাহু
৩. ‘সন্নিহিত বাহু (adjacent side)’, যা প্রদত্ত কোণ সৃষ্টিকারী একটি রেখাংশ।

| ∠PON কোণের জন্য অতিভুজ OP, সন্নিহিত বাহু ON, বিপরীত বাহু PN | ∠OPN কোণের জন্য অতিভুজ OP, সন্নিহিত বাহু PN, বিপরীত বাহু ON |
জ্যামিতিক চিত্রের শীর্ষবিন্দু চিহ্নিত করার জন্য বড় হাতের বর্ণ ও বাহু নির্দেশ করতে ছোট হাতের বর্ণ ব্যবহার করা হয়। কোণ নির্দেশের জন্য প্রায়শই গ্রিক বর্ণ ব্যবহৃত হয়। গ্রিক বর্ণমালার ছয়টি বহুল ব্যবহৃত বর্ণ হলো:
|
alpha α |
beta B | gamma y | theta 8 | phi ∅ | omega w |
| আলফা | বিটা | গামা | থিটা | ফাই |
ওমেগা |
প্রাচীন গ্রিসের বিখ্যাত গণিতবিদদের হাত ধরেই জ্যামিতি ও ত্রিকোণমিতিতে গ্রিক বর্ণগুলোর ব্যবহার হয়ে আসছে।
উদাহরণ ১.
8 কোণের জন্য অতিভুজ, সন্নিহিত বাহু ও বিপরীত বাহু চিহ্নিত কর।
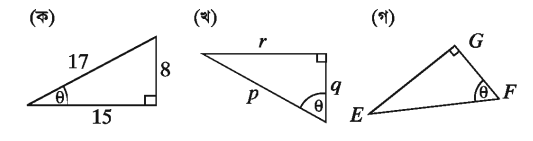
সমাধান :
ক) অতিভুজ 17 একক
বিপরীত বাহু ৪ একক
সন্নিহিত বাহু 15 একক
খ) অতিভুজ p
বিপরীত বাহু r
সন্নিহিত বাহু q
গ) অতিভুজ EF
বিপরীত বাহু EG
সন্নিহিত বাহু FG
উদাহরণ ২.
α ও B কোণের জন্য অতিভুজ, সন্নিহিত বাহু ও বিপরীত বাহুর দৈর্ঘ্য নির্ণয় কর।
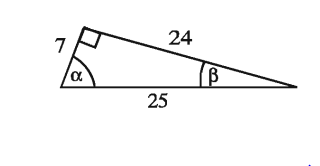
সমাধান :
ক) a কোণের জন্য
অতিভুজ 25 একক
বিপরীত বাহু 24 একক
সন্নিহিত বাহু 7 একক
খ) B কোণের জন্য
অতিভুজ 25 একক
বিপরীত বাহু 7 একক
সন্নিহিত বাহু 24 একক
সদৃশ সমকোণী ত্রিভুজের বাহুগুলোর অনুপাতসমূহের ধ্রুবতা
মনে করি, ∠XOA একটি সূক্ষ্মকোণ। OA বাহুতে যেকোনো একটি বিন্দু P নিই। P থেকে OX বাহু পর্যন্ত PM লম্ব টানি। ফলে একটি সমকোণী ত্রিভুজ POM গঠিত হলো। এই ∆POM এর PM, OM ও OP বাহুগুলোর যে তিনটি অনুপাত পাওয়া যায় এদের মান OA বাহুতে নির্বাচিত P বিন্দুর অবস্থানের ওপর নির্ভর করে না।
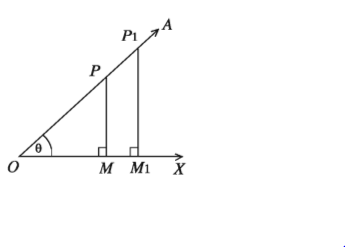
∠XOA কোণের OA বাহুতে যেকোনো বিন্দু P ও P1 থেকে OX বাহু পর্যন্ত যথাক্রমে PM ও PM লম্ব অঙ্কন করলে ∆POM O ও ∆POM, দুইটি সদৃশ সমকোণী ত্রিভুজ গঠিত হয়।
এখন, ∆POM ও ∆POM সদৃশ হওয়ায়,
PM/P1M1 = OP/OP₁
বা, PM /OP = P₁M₁/OP1
OM/OM1 = OP/OP₁
বা, OM/OP = OM1/OP1
PM/P1M1 = OM/OM1
বা, PM/OM = P1M1/OM1
অর্থাৎ, অনুপাতসমূহের প্রত্যেকটি ধ্রুবক। এই অনুপাতসমূহকে ত্রিকোণমিতিক অনুপাত বলে।
