আজকে আমাদের আলোচনার বিষয়ঃ অনুপাত ও সমানুপাতের ধর্ম। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

অনুপাত ও সমানুপাতের ধর্ম
(i) a : b = x : y এবং c : d = x : y হলে, a : b = c : d
(ii) a : b = b : a হলে, a = b
(iii) a: b = x : y হলে, b : a = y : x (ব্যস্তকরণ)
(iv) a:b = x y হলে, a : x = b : y (একান্তরকরণ)
(v) a : b = c : d হলে, ad = bc (আড়গুণন
(vi) a : b = x : y হলে, a + b : b = x + y : y ( যোজন )
এবং a – b : b = x – y :y (বিয়োজন)
(vii) a/b = c/d হলে, (a+b)/(a-b) = (c+d)/(c-d) (যোজন ও বিয়োজন)
জ্যামিতিক সমানুপাত (Geometric proportions)
আমরা ত্রিভুজক্ষেত্রের ক্ষেত্রফল নির্ণয় করতে শিখেছি। এ থেকে দুইটি প্রয়োজনীয় অনুপাতের ধারণা তৈরি করা যায়।
১. দুইটি ত্রিভুজক্ষেত্রের উচ্চতা সমান হলে, এদের ক্ষেত্রফল ও ভূমি সমানুপাতিক ।
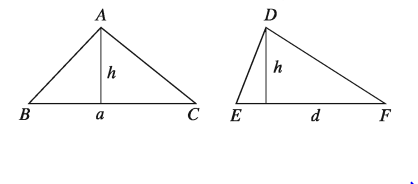
মনে করি, ত্রিভুজক্ষেত্র ABC ও DEF এর ভূমি যথাক্রমে BC = a, EF = d এবং উভয় ক্ষেত্রের উচ্চতা h
সুতরাং, ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল = 1/2 × a × h, ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল = 1/2 × d × h
অতএব, ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল: ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল
= 1/2 × a × h : 1/2 × d × h =a: d = BC : EF
২. দুইটি ত্রিভুজক্ষেত্রের ভূমি সমান হলে, এদের ক্ষেত্রফল ও উচ্চতা সমানুপাতিক ।
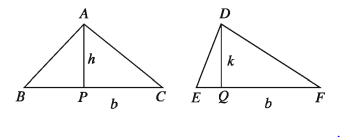
মনে করি, ত্রিভুজক্ষেত্র ABC ও DEF এর উচ্চতা যথাক্রমে AP = h, DQ = k এবং উভয় ক্ষেত্রের ভূমি b
সুতরাং, ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল = 1/2 × b × h, ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল = 1/2 × b × k
অতএব, ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল: ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল
= 1/2 × b × h : 1/2 × b × k = h : k = AP : DQ
উপপাদ্য ২৮.
ত্রিভুজের যেকোনো বাহুর সমান্তরাল সরলরেখা ঐ ত্রিভুজের অপর বাহুদ্বয়কে বা এদের বর্ধিতাংশদ্বয়কে সমান অনুপাতে বিভক্ত করে।
বিশেষ নির্বচন :
ABC ত্রিভুজের BC বাহুর সমান্তরাল DE রেখাংশ AB ও AC বাহুদ্বয়কে (চিত্র-১) অথবা এদের বর্ধিতাংশদ্বয়কে (চিত্র-২) যথাক্রমে D ও E বিন্দুতে ছেদ করেছে।
প্ৰমাণ করতে হবে যে, AD: DB = AE EC
অঙ্কন :
B E এবং C, D যোগ করি।
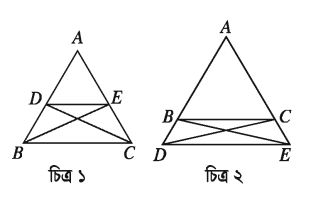
প্ৰমাণ :
ধাপ ১.
∆ADE এবং ∆BDE একই উচ্চতাবিশিষ্ট
∆ADE/∆BDE = AD/ DB [একই উচ্চতাবিশিষ্ট ত্রিভুজসমূহের ক্ষেত্রফল ভূমির সমানুপাতিক ]
ধাপ ২.
∆ADE এবং ∆DEC একই উচ্চতাবিশিষ্ট
∆ADE/∆DEC = AE/EC [একই উচ্চতাবিশিষ্ট ত্রিভুজসমূহের ক্ষেত্রফল ভূমির সমানুপাতিক]
ধাপ ৩.
কিন্তু ∆BDE = ∆DEC [একই ভূমি DE ও একই সমান্তরাল রেখাযুগলের মধ্যে অবস্থিত]
∆ADE/ ∆BDE = ∆ADE/∆DEC
ধাপ ৪.
অতএব,
AD/DB = AE/EC
অর্থাৎ, AD : DB = AE : EC
অনুসিদ্ধান্ত ১.
ABC ত্রিভুজের BC বাহুর সমান্তরাল কোনো রেখা যদি AB ও AC বাহুকে যথাক্রমে D ও E বিন্দুতে ছেদ করে, তবে AB AD AC AB AE এবং BD AC CE হবে।
অনুসিদ্ধান্ত ২.
ত্রিভুজের কোনো বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত অপর এক বাহুর সমান্তরাল রেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে।
উপপাদ্য ২৮ এর বিপরীত প্রতিজ্ঞাও সত্য। অর্থাৎ কোনো সরলরেখা একটি ত্রিভুজের দুই বাহুকে অথবা এদের বর্ধিতাংশদ্বয়কে সমান অনুপাতে বিভক্ত করলে উক্ত সরলরেখা ত্রিভুজটির তৃতীয় বাহুর সমান্তরাল হবে। নিচে প্রতিজ্ঞাটি প্রমাণ করা হলো।

উপপাদ্য ২৯.
কোনো সরলরেখা একটি ত্রিভুজের দুই বাহুকে অথবা তাদের বর্ধিতাংশদ্বয়কে সমান অনুপাতে বিভক্ত করলে উক্ত সরলরেখা ত্রিভুজটির তৃতীয় বাহুর সমান্তরাল।
বিশেষ নির্বচন:
DE রেখাংশ ABC ত্রিভুজের AB ও AC বাহুদ্বয়কে অথবা এদের বর্ধিতাংশদ্বয়কে সমান অনুপাতে বিভক্ত করেছে।
অর্থাৎ AD : DB = AE : EC
প্রমাণ করতে হবে যে, DE এবং BC সমান্তরাল।
অঙ্কন :
B, E এবং C, D যোগ করি।

প্ৰমাণ :
ধাপ ১.
∆ADE/ ∆BDE = AD/DB [ত্রিভুজ দুইটি একই উচ্চতাবিশিষ্ট]
এবং ∆ADE /∆DEC = AE/EC [ত্রিভুজ দুইটি একই উচ্চতাবিশিষ্ট]
ধাপ ২.
কিন্তু AD/DB = AE/ EC [স্বীকার]
ধাপ ৩.
অতএব, ∆ADE/∆BDE = ∆ADE/∆DEC [(১) এবং (২) থেকে]
∆BDE = ∆DEC
ধাপ ৪.
কিন্তু ∆BDE এবং ∆DEC একই ভূমি DE এর একই পাশে অবস্থিত। সুতরাং তারা একই সমান্তরাল যুগলের মধ্যে অবস্থিত। .. BC ও DE সমান্তরাল।
উপপাদ্য ৩০.
ত্রিভুজের যেকোনো কোণের অন্তসমদ্বিখণ্ডক বিপরীত বাহুকে উক্ত কোণ সংলগ্ন বাহুদ্বয়ের অনুপাতে অন্তর্বিভক্ত করে।
বিশেষ নির্বচন
মনে করি, AD রেখাংশ ∆ABC এর অন্তঃস্থ ∠A কোণকে সমদ্বিখণ্ডিত করে BC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, BD : DC = BA: AC
অঙ্কন:
DA রেখাংশের সমান্তরাল করে C বিন্দু দিয়ে CE রেখাংশ অঙ্কন করি, যেন তা বর্ধিত BA বাহুকে E বিন্দুতে ছেদ করে।
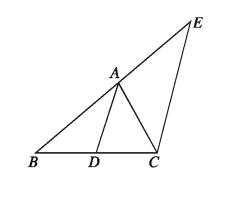
প্ৰমাণ:
ধাপ ১.
যেহেতু DA || CE এবং BE এদের ছেদক [অঙ্কন]
∠AEC = ∠BAD [অনুরূপ কোণ]
আবার DA || CE এবং AC এদের ছেদক
∠ACE = ∠CAD [একান্তর কোণ]
ধাপ ২.
কিন্তু ∠BAD = ∠CAD [স্বীকার]
∠AEC = ∠ACE
সুতরাং AC = AE [অধ্যায় ৬ উপপাদ্য ৮]
ধাপ ৩.
আবার যেহেতু, DA || CE
সুতরাং BD/DC = BA/AE [ধাপ ২]
ধাপ ৪.
কিন্তু AE = AC
BD/DC = BA/AC
উপপাদ্য ৩১.
ত্রিভুজের যেকোনো বাহু অপর দুই বাহুর অনুপাতে অন্তর্বিভক্ত হলে, বিভাগ বিন্দু থেকে বিপরীত শীর্ষ বিন্দু পর্যন্ত অঙ্কিত রেখাংশ উক্ত শীর্ষকোণের সমদ্বিখণ্ডক হবে।
বিশেষ নির্বচন
মনে করি, ABC ত্রিভুজের A বিন্দু থেকে অঙ্কিত AD সরলরেখাংশ BC বাহুকে D বিন্দুতে এরূপে অন্তঃস্থভাবে বিভক্ত করেছে যে, BD: DC = BA : AC
প্রমাণ করতে হবে যে, AD রেখাংশ ∠BAC এর সমদ্বিখণ্ডক অর্থাৎ, ∠BAD = ∠CAD
অঙ্কন:
DA রেখাংশের সমান্তরাল করে C বিন্দু দিয়ে CE রেখাংশ অঙ্কন করি, যেন তা বর্ধিত BA বাহুকে E বিন্দুতে ছেদ করে।

প্ৰমাণ
ধাপ ১.
∆BCE এর DA || CE [অঙ্কন]
BA: AE = BD : DC [উপপাদ্য ২৮]
ধাপ ২.
কিন্তু BD : DC = BA : AC [স্বীকার]
BA: AE = BA: AC [ধাপ ১ ও ধাপ ২ থেকে]
AE = AC
অতএব, ∠ACE = ∠AEC [সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণ দুইটি সমান]
ধাপ ৩.
কিন্তু ∠AEC = ∠BAD [অনুরূপ কোণ]
এবং ∠ACE = ∠CAD [একান্তর কোণ]
অতএব, ∠BAD = ∠CAD [ধাপ ২ থেকে]
.: AD রেখাংশ ∠BAC এর সমদ্বিখণ্ডক।
