নির্দিষ্ট অনুপাতে রেখাংশের বিভক্তিকরণ

আজকে আমাদের আলোচনার বিষয়ঃ নির্দিষ্ট অনুপাতে রেখাংশের বিভক্তিকরণ। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

 

 

নির্দিষ্ট অনুপাতে রেখাংশের বিভক্তিকরণ

দুইটি রাশির তুলনা করার জন্য এদের অনুপাত বিবেচনা করা হয়। অনুপাত নির্ণয়ের জন্য রাশি দুইটি একই এককে পরিমাপ করতে হয়।

সমতলে দুইটি ভিন্ন বিন্দু A ও B এবং m ও n যেকোনো স্বাভাবিক সংখ্যা হলে স্বীকার করে নিই যে, রেখায় এমন অনন্য বিন্দু X আছে যে, X বিন্দুটি A ও B বিন্দুর অন্তবর্তী এবং AX : XB = m : n

 

 

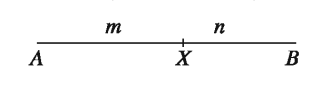
ওপরের চিত্রে, AB রেখাংশ X বিন্দুতে m : n অনুপাতে অন্তর্বিভক্ত হয়েছে। তাহলে, AX : XB = m: n

সম্পাদ্য ১২.

কোনো রেখাংশকে একটি নির্দিষ্ট অনুপাতে অন্তর্বিভক্ত করতে হবে।

বিশেষ নির্বচন:

মনে করি, AB রেখাংশকে m n অনুপাতে অন্তর্বিভক্ত করতে হবে।

অঙ্কন:

A বিন্দুতে যেকোনো কোণ ∠BAX অঙ্কন করি এবং AX রশ্মি থেকে পরপর AE = m এবং EC = n অংশ কেটে নিই । B, C যোগ করি। E বিন্দু দিয়ে CB এর সমান্তরাল ED রেখাংশ অঙ্কন করি যা AB কে D বিন্দুতে ছেদ করে । তাহলে AB রেখাংশ D বিন্দুতে  m : n অনুপাতে অন্তর্বিভক্ত হলো।

 

 

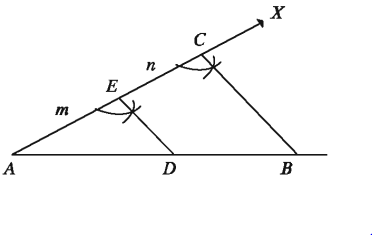
প্রমাণ:

যেহেতু DE রেখাংশ ABC ত্রিভুজের এক বাহু BC এর সমান্তরাল,

AD : DB = AE : EC = m : n

 

 

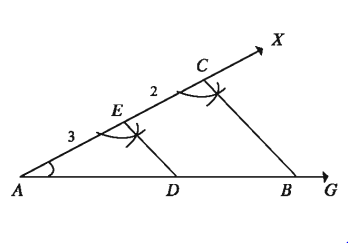
সমাধান:

যেকোনো একটি রশ্মি AG আঁকি এবং AG থেকে 7 সে.মি. সমান রেখাংশ AB নিই। A বিন্দুতে যেকোনো কোণ ∠BAX অঙ্কন করি। AX রশ্মি থেকে AE = 3 সে.মি. কেটে নিই এবং EX থেকে EC = 2 সে.মি. কেটে নিই। B, C যোগ করি। E বিন্দুতে ∠ACB এর সমান ∠AED অঙ্কন করি যার ED রেখা AB কে D বিন্দুতে ছেদ করে। তাহলে AB রেখাংশ D বিন্দুতে 3 : 2 অনুপাতে অন্তর্বিভক্ত হলো।