আজকে আমরা অনুপাত, সদৃশতা ও প্রতিসমতার অনুশীলনী ২ আলোচনা করবো। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

অনুপাত, সদৃশতা ও প্রতিসমতার অনুশীলনী ২
১. ∆ABC এ BC এর সমান্তরাল DE রেখা AB ও AC কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে
(i) ∆ABC ও ∆ADE পরস্পর সদৃশ।
(ii) AD/BD = CE/AE
(iii) ∆ABC/∆ADE = BC2/DE2
নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
পাশের চিত্রের তথ্যানুসারে ২ ও ৩ নং প্রশ্নের উত্তর দাও:
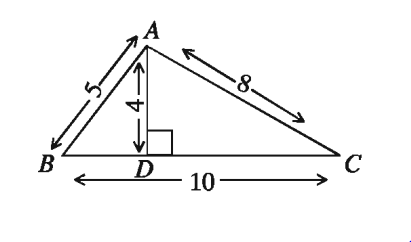
২. ∆ABC এর উচ্চতা ও ভূমির অনুপাত কত?
ক) 1/2
খ) 4/5
গ) 2/5
ঘ) 5/4
৩. ∆ABD এর ক্ষেত্রফল কত বর্গ একক?
ক) 6
খ) 20
গ) 40
ঘ) 50
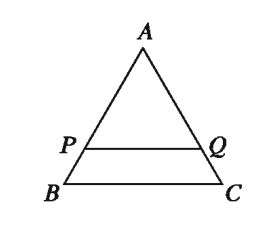
8. ∆ABC এ PQ || BC হলে নিচের কোনটি সঠিক?
ক) AP : PB = AQ : QC
খ) AB : PQ = AC : PQ
গ) AB : AC = PQ : BC
ঘ) PQ : BC = BP : BQ
৫. প্রমাণ কর যে, দুইটি ত্রিভুজের প্রত্যেকটি যদি তৃতীয় একটি ত্রিভুজের সদৃশ হয়, তবে তারা পরস্পর সদৃশ।
৬. প্রমাণ কর যে, দুইটি সমকোণী ত্রিভুজের একটির একটি সূক্ষ্মকোণ অপরটির একটি সূক্ষ্মকোণের সমান হলে, ত্রিভুজ দুইটি সদৃশ হবে।
৭. প্রমাণ কর যে, সমকোণী ত্রিভুজের সমকৌণিক শীর্ষ থেকে অতিভুজের উপর লম্ব আঁকলে যে দুইটি সমকোণী ত্রিভুজ উৎপন্ন হয়, তারা পরস্পর সদৃশ এবং প্রত্যেকে মূল ত্রিভুজের সদৃশ।
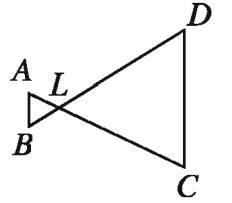
৮. পাশের চিত্রে, ∠B = ∠D এবং CD = 4AB। প্রমাণ কর যে, BD = 5BL
৯. ABCD সামন্তরিকের A শীর্ষ দিয়ে অঙ্কিত একটি রেখাংশ BC বাহুকে M বিন্দুতে এবং DC বাহুর বর্ধিতাংশকে N বিন্দুতে ছেদ করে। প্রমাণ কর যে, BM x DN একটি ধ্রুবক।
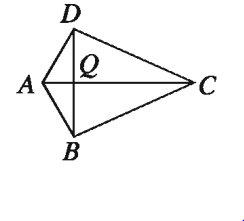
১০. পাশের চিত্রে BD ⊥ AC এবং DQ = BQ = 2AQ = ½QC প্রমাণ কর যে, DA ⊥ DC
১১. ∆ABC ও ∆DEF এর ∠A = ∠D। প্রমাণ কর যে, ∆ABC : ∆DEF = AB . AC : DE.DF
১২. ∆ABC এর ∠A এর সমদ্বিখণ্ডক AD, BC কে D বিন্দুতে ছেদ করেছে। DA এর সমান্তরাল CE রেখাংশ বর্ধিত BA বাহুকে E বিন্দুতে ছেদ করেছে।
ক) তথ্য অনুসারে চিত্রটি অঙ্কন কর।
খ) প্রমাণ কর যে, BD : DC = BA: AC
গ) BC এর সমান্তরাল কোনো রেখাংশ AB ও AC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করলে, প্রমাণ কর যে, BD: DC = BP : CQ
১৩. চিত্রে ABC এবং DEF দুইটি সদৃশ ত্রিভুজ।
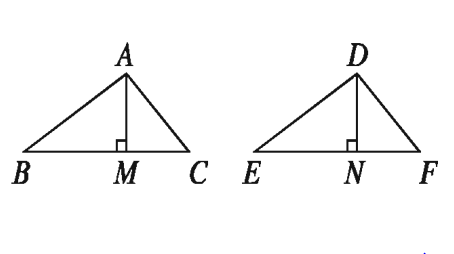
ক) ত্রিভুজ দুইটির অনুরূপ বাহু ও অনুরূপ কোণগুলোর নাম লিখ।
প্রমাণ কর যে, ∆ABC/∆DEF = AB2/DE2 = AC2/DF2 = BC2/EF2
গ) যদি BC = 3 সে.মি., EF = 8 সে.মি., ∠B = 60°, BC/AB = 3/2 এবং ∆ABC এর ক্ষেত্রফল 3 বর্গ সে.মি. হয়, তবে ∆DEF অঙ্কন কর এবং এর ক্ষেত্রফল নির্ণয় কর।
