আজকে আমাদের আলোচনার বিষয়ঃ প্রতিসমতা জ্যামিতি। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

প্রতিসমতা জ্যামিতি
প্রতিসমতা হলো কোনো বস্তুকে প্রতিফলন, ঘূর্ণন, আরোহী পদ্ধতি ইত্যাদি বিবিধ রূপান্তর প্রক্রিয়ার মাধ্যমে বস্তুটির একই (অপরিবর্তিত) আকার ও আকৃতি দেখানো।
প্রতিসমতা একটি প্রয়োজনীয় জ্যামিতিক ধারনা যা প্রকৃতিতে বিদ্যমান এবং যা আমাদের কর্মকান্ডে প্রতিনিয়ত ব্যবহার করে থাকি। প্রতিসমতার ধারনাকে শিল্পী, কারিগর, ডিজাইনার, ছুতাররা প্রতিনিয়ত ব্যবহার করে থাকেন। গাছের পাতা, ফুল, মৌচাক, ঘরবাড়ি, টেবিল, চেয়ার সব কিছুর মধ্যে প্রতিসমতা বিদ্যমান। যদি কোনো সরলরেখা বরাবর কোনো চিত্র ভাঁজ করলে তার অংশ দুইটি সম্পূর্ণভাবে মিলে যায় সেক্ষেত্রে সরলরেখাটিকে প্রতিসাম্য রেখা বলা হয়।

উপরের চিত্রগুলোর প্রতিটির প্রতিসাম্য রেখা রয়েছে।
সুষম বহুভুজের প্রতিসাম্য রেখা ( Lines of symmetry of a regular polygon )
বহুভুজ কতকগুলো রেখাংশ দ্বারা আবদ্ধ চিত্র। বহুভুজের রেখাংশগুলোর দৈর্ঘ্য সমান ও কোণগুলো সমান হলে একে সুষম বহুভুজ বলা হয়। ত্রিভুজ হলো সবচেয়ে কম সংখ্যক রেখাংশ দিয়ে গঠিত বহুভুজ। সমবাহু ত্রিভুজ হলো তিন বাহু বিশিষ্ট সুষম বহুভুজ। সমবাহু ত্রিভুজের বাহু ও কোণগুলো সমান। চার বাহুবিশিষ্ট সুষম বহুভুজ হলো বর্গক্ষেত্র। বর্গক্ষেত্রের বাহু ও কোণগুলো সমান। অনুরূপভাবে, সুষম পঞ্চভুজ ও সুষম ষড়ভুজের বাহু ও কোণগুলো সমান ।
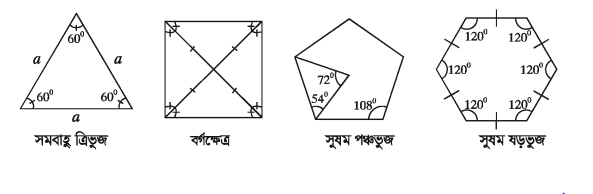
প্রত্যেক সুষম বহুভুজ একটি প্রতিসম চিত্র। সুতরাং এদের প্রতিসাম্য রেখার সম্পর্কে জানা আবশ্যক । সুষম বহুভুজের অনেক বাহুর পাশাপাশি একাধিক প্রতিসাম্য রেখা রয়েছে।
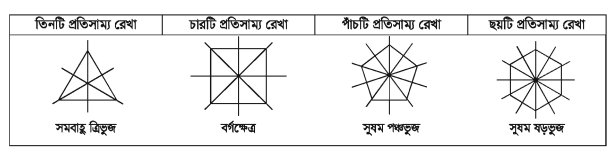
যে রেখাটির উপর চিত্রটি দুই ভাগে বিভক্ত হয়ে প্রতিফলন প্রতিসমতা সৃষ্টি করে তাকে বলা হয় প্রতিসাম্য রেখা। এ ধরনের প্রতিসমতার ধারণার সাথে আয়নার প্রতিফলনের সম্পর্ক রয়েছে। কোনো জ্যামিতিক চিত্রের প্রতিসাম্য রেখা তখনই থাকে, যখন তার অর্ধাংশের প্রতিচ্ছবি বাকি অর্ধাংশের সাথে মিলে যায়। এজন্য প্রতিসাম্য রেখা নির্ণয়ে কাল্পনিক আয়নার অবস্থান রেখার সাহায্য নেওয়া হয়। রেখা প্রতিসমতাকে প্রতিফলন প্রতিসমতাও বলা হয়।
