আজকে আমাদের আলোচনার বিষয়ঃ জ্যামিতিক প্যাটার্ন । এটি অষ্টম শ্রেনী গণিতের প্যাটার্ন অংশের অন্তর্গত।
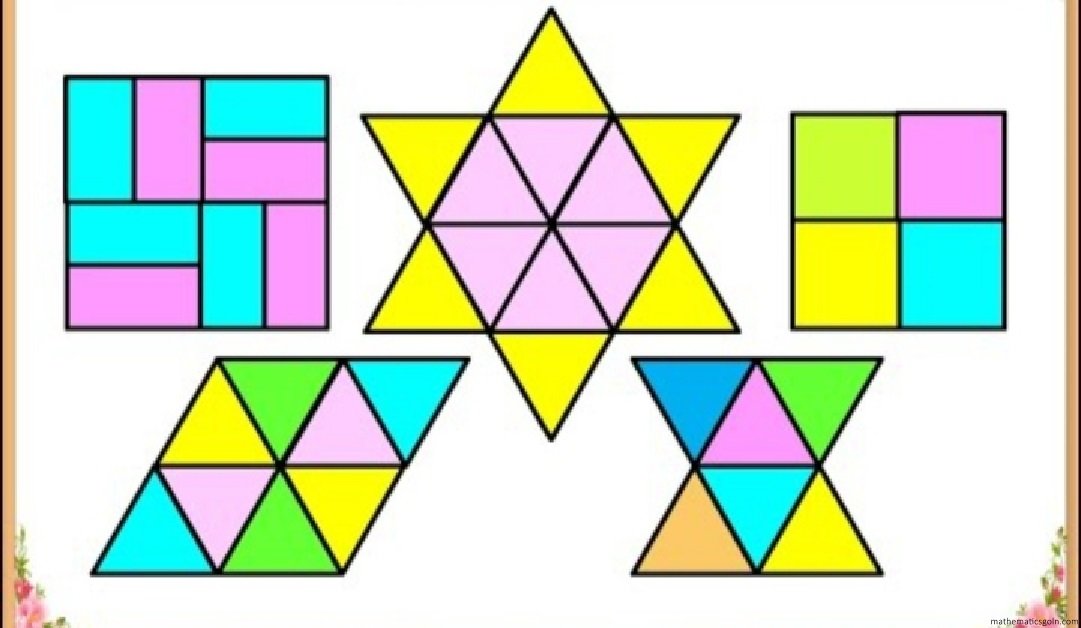
জ্যামিতিক প্যাটার্ন
চিত্রের বর্ণগুলো সমান দৈর্ঘ্যের রেখাংশের দ্বারা তৈরি করা হয় । এ রকম কয়েকটি অঙ্কের চিত্র লক্ষ করি :
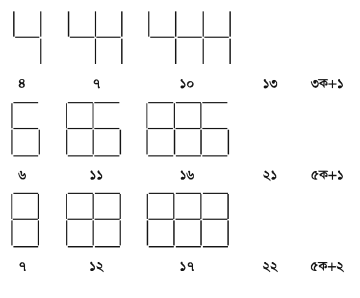
চিত্রগুলো তৈরি করতে কতগুলো রেখাংশ প্রয়োজন এর প্যাটার্ন লক্ষ করি। ‘ক’ সংখ্যক অঙ্ক তৈরির জন্য রেখাংশের সংখ্যা প্রতি প্যাটার্নের শেষে বীজগণিতীয় রাশির সাহায্যে দেখানো হয়েছে ।
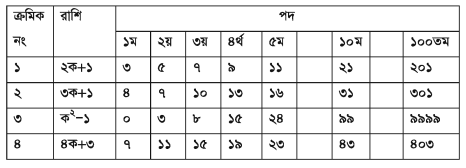
উদাহরণ ৪ ।
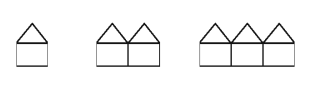
উপরের জ্যামিতিক চিত্রগুলো একটি প্যাটার্ন তৈরি করছে যা সমান দৈর্ঘ্যের কাঠি দিয়ে তৈরি ।
ক. প্যাটার্নে চতুর্থ চিত্রটি তৈরি করে কাঠির সংখ্যা নির্ণয় কর ।
খ. প্যাটার্নটি কোন বীজগণিতীয় রাশিকে সমর্থন করে তা যুক্তিসহ উপস্থাপন কর ।
গ. প্যাটার্নটির প্রথম পঞ্চাশটি চিত্র তৈরি করতে মোট কতটি কাঠি দরকার হবে তা নির্ণয় কর ।
সমাধান :
(ক) উদ্দীপকের আলোকে চতুর্থ প্যাটার্নটি নিম্নরূপ
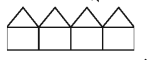
প্যাটার্নটিতে সমান দৈর্ঘ্যের কাঠির সংখ্যা ২১
(খ) ১ম চিত্রে কাঠির সংখ্যা = ৬ = ৫+১ = ৫ x ১ +১
২য় চিত্রে কাঠির সংখ্যা = ১১ =১০+১ = ৫ x ২ +১
৩য় চিত্রে কাঠির সংখ্যা = ১৬ = ১৫+১ = ৫ x ৩ +১
৪র্থ চিত্রে কাঠির সংখ্যা = ২১ = ২০+১ = ৫ x ৪ +১
একই ভাবে ক-তম চিত্রে, কাঠির সংখ্যা = ৫ x ক+১ = ৫ক+১
.: প্যাটার্নগুলো (৫ক+১) বীজগাণিতিক রাশি দ্বারা প্রকাশ করা যায় ।
(গ) ‘খ’ অংশ থেকে পাই
প্যাটার্নটির বীজগাণিতিক রাশি ৫ক+১
৫০ তম প্যাটার্নে প্রয়োজনীয় কাঠির সংখ্যা = ৫ x ৫০+১ = ২৫০+১ = ২৫১
এখন, প্যাটার্নগুলোর কাঠির সংখ্যাগুলোর সমষ্টি = ৬+১১+১৬+২১+…+২৫১
এখানে, ১ম পদ = ৬
শেষ পদ = ২৫১
পদ সংখ্যা = ৫০
:: সমষ্টি = (৬ + ২৫১)/২ × ৫০ [সমষ্টি = (১ম সংখ্যা + শেষ সংখ্যা)/২ x পদ সংখ্যা]
= ২৫৭ × ২৫
= ৬৪২৫
:: ৫০টি প্যাটার্ন তৈরিতে প্রয়োজনীয় কাঠির সংখ্যা ৬৪২৫
