সেট প্রক্রিয়ার কতিপয় প্রতিজ্ঞা

আজকে আমরা আলোচনা করবো  সেট প্রক্রিয়ার কতিপয় প্রতিজ্ঞা সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

 

 

সেট প্রক্রিয়ার কতিপয় প্রতিজ্ঞা

এখানে প্রত্যেক ক্ষেত্রে / সার্বিক সেট এবং A, B, C সেটগুলো U এর উপসেট।

ক) বিনিময় বিধি

(১) AUB = BUA

(২) A∩B = B∩A

খ) সংযোগ বিধি

(১) (AUB) UC = AU (BUC)

(২) (A∩B∩C = A∩ (B∩C)

গ) বন্টন বিধি

(১) AU (B∩C) = (AUB)∩ (AUC)

(২) An (BUC) – (AB) U (ANC)

ঘ) ডি মরগ্যানের সূত্র

(১) (AUB)’= A’∩B’

(২) A∩B = A’UB’

ঙ) অন্যান্য সূত্র

(১) AUA = A, A∩A = A

(২) AU∅ = A, A∩∅ =∅

(৩) AUU = U, A∩U = A

(8) A⊆B = B’⊆ A’

(৫) A⊆B ⇒ AUB = B

(৬) (A⊆B ) ⇒ A∩B =A

(৭) A⊆AUB

(৮) A∩B⊆A

(৯) A\ B = A∩B’

 

 

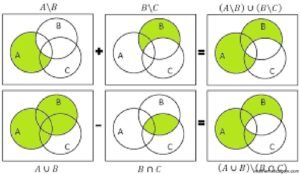
বিনিময় বিধির প্রতিজ্ঞা দুইটি যাচাইকরণ

নিচের বামের চিত্রে গাঢ় অংশটুকু AUB এবং BUA উভয় সেটই নির্দেশ করে। সুতরাং এক্ষেত্রে দেখা যাচ্ছে AUB = BUA। নিচের ডানের চিত্রে পাঢ় অংশটুকু An B এবং BnĀ উভয় সেটই নির্দেশ করে। সুতরাং এক্ষেত্রে দেখা যাচ্ছে A∩B = B∩A

উপরে ভেনচিত্রের সাহায্যে যাচাই করা হয়েছে। এবার সুনির্দিষ্ট উদাহরণ নিয়ে দেখা যাক।

মনে করি A = {1, 2, 4} এবং B = {2,3,5} দুইটি সেট।

তাহলে, AUB = (1, 2, 4 ) ( 235 ) – (1, 2, 3, 4, 5)।

আবার, BUA = (2, 3, 5) U (1, 2, 4 ) = (1, 2, 3, 4, 5 )

সুতরাং এক্ষেত্রে AUB BA

অন্য দিকে, A∩B = {1, 2, 4} {2,3,5} = {2}

এবং Bn A = { 2, 3, 5 ) n (1, 2, 4 ) – ( 2 ) ।

সুতরাং এক্ষেত্রে A∩B = B∩A

 

সংযোগ বিধির প্রতিজ্ঞা দুইটির যাচাইকরণ

নিচের বামের চিত্রে গাঢ় অংশটুকু AU (BUC) এবং (AUB)UC উভয় সেটই নির্দেশ করে। সুতরাং এক্ষেত্রে AU (BUC) = (AUB) UC নিচের ডানের চিত্রে গাঢ় অংশটুকু An (BAC) এবং (A∩B)∩C উভয় সেটই নির্দেশ করে। সুতরাং এক্ষেত্রে ( An BNC = An (BC)।

 

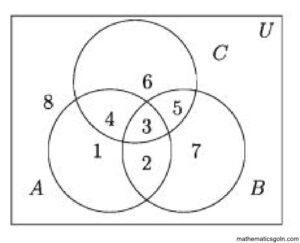
উপরে ভেনচিত্রের সাহায্যে যাচাই করা হয়েছে। এবার সুনির্দিষ্ট উদাহরণ নিয়ে দেখা যাক।

মনে করি A = {a, b, c, d), B= [h, c, / } এবং C = { c, d, g} ।

তাহলে, BUC- (b, a. f) (adg) – (bc, d, J.g)

এবং AU (BUC) = {a, b, c, d} U{b, c, d, f, s} = {a, b, c, d, fig} 1

আবার, AUB = {a, had Utha f} – (a,b,c,d )

এবং (AUB) UC = {a, b, c, d, f} { c, d, g} = {a,b,c,d,f,g}”

সুতরাং এক্ষেত্রে (AUB) UC = AU (BUC)।

আবার, BnC = {b, c, f}n (eds) = (c)

এবং An (BAC) = (a, bed) n (c) = (0)

আবার, A∩ B = {a,b,c,d}^{ba f} = {bc}

এবং (A∩B)n C = {bc}n {edg} = {c} +

সুতরাং এক্ষেত্রে An (BAC) = (AB) NCT

দ্রষ্টব্য:

সেটের সংযোগ ও হেন প্রক্রিয়া দুইটির প্রতিটি অপরটির প্রেক্ষিতে বন্টন নিয়ম মেনে চলে।

 

 

প্রতিজ্ঞা ১ (ডি মরগ্যানের সূত্র),

সার্বিক সেট U এর যেকোনো উপসেট A ও B এর জন্য

ক) (AUB)’ = A’∩B’

খ) (A∩B)’ = A’ UB’

প্রমাণ:

কেবল প্রথমটির প্রমাণ নিচে দেখানো হয়েছে।

ক) মনে করি, X ∊ (AUB)’। তাহলে,X ∉ AUB
→ X ∉ A এবং X ∉B
→ X ∊A’ এবং X ∊ B’
→ X ∊A’∩B’
→ (AUB)’⊆ A’∩B’

আবার মনে করি, X∈ A’∩ B’। তাহলে, x∈ A’ এবং x ∈ B’
x ∉A এবং x ∉ B
x ∉ AUB
x ∉ (AUB)’

A’∩B’= (AUB)’

সুতরাং (AUB)’ = A’∩B’

প্রতিজ্ঞা ২

সার্বিক সেট U এর যেকোনো উপসেট A ও B এর জন্য A \B = A∩B’

প্রমাণ:

মনে করি, x ∈ A \B। তাহলে, x ∈ A এবং x ∉ B
⇒ x ∈ A এবং x ∈ B’
⇒ x ∈ A∩ B’
A∩ B’⊆ A\B

আবার মনে করি, x ∈ A∩B’। তাহলে, x ∈ A এবং x ∈ B’।
⇒ x ∈ A এবং x ∈ B
⇒ x ∈ A\B

A∩ B’ ⊆ A\B

OR, A\B = A∩ B’

প্রতিজ্ঞা ৩

যেকোনো সেট A, B, C এর জন্য

ক) Ax (B∩C) = (A x B) ∩ (A x C)

খ) Ax (BUC) = (A x B) U (A x C)

প্রমাণ:

(কেবল প্রথমটির প্রমাণ নিচে দেখানো হয়েছে। পরেরটির প্রমাণ নিজে কর।)

ক) সংজ্ঞানুসারে, Ax (BNC)

= {(x, y): x∈ A, y∈ B∩C}

= {(x, y) : x Є A, y Є B এবং y ∈C}

= {(x, y) : (x, y) ∈ (AX B) এবং (x, y) ∈ AxC}

= {(x, y): (x, y) ∈ (Ax B) ∩ (Ax C)}

= Ax (B∩C) ∈ (Ax B)∩ (Ax C)

= (Ax B)∩(Ax C)

 

 

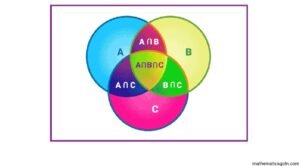
সেট প্রক্রিয়া সংক্রান্ত আরো কতিপয় প্রতিজ্ঞা

ক) A যেকোনো সেট হলে A⊆A

খ) ফাঁকা সেট ∅ যেকোনো সেট A এর উপসেট।

গ) A ও B যেকোনো সেট হলে A = B হবে যদি ও কেবল যদি A⊆B এবং B⊆A হয়।

ঘ) যদি A⊆Ø হয়, তবে A = Ø।

ঙ) যদি A⊆ B এবং B⊆C তবে, A⊆C’

চ) A ও B যেকোনো সেট হলে, An B⊆ A এবং AB⊆ B

ছ) A ও B যেকোনো সেট হলে, A ⊆AUB এবং B ⊆ AUB

ঘ) দেওয়া আছে, A⊆ Ø, আবার আমরা জানি, Ø ⊆ A। সুতরাং A = Ø

ছ) সেট সংযোগের সংজ্ঞানুযায়ী, A সেটের সকল উপাদান AUB সেটে থাকে। সুতরাং উপসেটের সংজ্ঞানুযায়ী A⊆ AUB একই যুক্তিতে B ⊆ AUB.

এক-এক মিল (One One Correspondence)

মনে করি, A = {a,b,c} তিনজন লোকের সেট এবং B = { 30, 40, 50 } ঐ তিনজন লোকের বয়সের সেট। অধিকন্তু মনে করি, a এর বয়স 30 বছর, b এর বয়স 40 বছর এবং c এর বয়স 50 বছর। বলা যায় যে, A সেটের সাথে B সেটের এক-এক মিল আছে।

 

 

সংজ্ঞা ১ (এক-এক মিল)

যদি A সেটের প্রতিটি উপাদানের সাথে B সেটের একটি ও কেবল একটি উপাদান এবং B সেটের প্রতিটি উপাদানের সাথে A সেটের একটি ও কেবল একটি উপাদানের মিল স্থাপন করা যায়, তবে তাকে A ও B এর মধ্যে এক-এক মিল বলা হয়। A ও B এর মধ্যে এক-এক মিলকে সাধারণত A + B লিখে প্রকাশ করা হয় এবং A সেটের কোনো সদস্য 1 এর সঙ্গে B সেটের যে সদস্য y এর মিল করা হয়েছে তা x + y লিখে বর্ণনা করা হয়।

 

সেট সংক্রান্ত গাণিতিক সমস্যা [1/2] :

 

সেট সংক্রান্ত গাণিতিক সমস্যা [2/2] :

 

আরও দেখুনঃ

• গনিতের সেট