আজকে আমরা আলোচনা করবো সমতুল সেট সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

সমতুল সেট
ধরি, A = {1, 2, 3} এবং B = { a, b, c} দুইটি সেট। নিচের চিত্রে A ও B সেটদ্বয়ের মধ্যে একটি এক এক মিল স্থাপন করে দেখানো হলো:
সংজ্ঞা ২ (সমতুল সেট)
যেকোনো সেট A ও B এর মধ্যে যদি একটি এক-এক মিল A + B বর্ণনা করা যায়, তবে A ও B কে সমতুল সেট বলা হয়। A ও B কে সমতুল বোঝাতে A ~ B লেখা হয়। A ~ B হলে, এদের যেকোনো একটিকে অপরটির সাথে সমতুল বলা হয়। লক্ষণীয় যে, যেকোনো সেট A, B ও C এর জন্য
ক) A ~ A
খ) A ~ B হলে B ~ A
গ) A~ B এবং B ~C হলে A ~ C
উদাহরণ ১৩.
দেখাও যে, A = {1, 2, 3, …, n} এবং B = {1, 3, 5, 2n – 1} সেটদ্বয় সমতুল, যেখানে n একটি স্বাভাবিক সংখ্যা।
সমাধান:
A ও B সমতুল, কারণ সেট দুইটির মধ্যে নিচের মতো একটি এক-এক মিল রয়েছে।
মন্তব্য:
উপরে চিত্রিত এক-এক মিলটিকে A + B k 2k 1, k∈ A দ্বারা বর্ণনা করা যায়।
উদাহরণ ১৪.
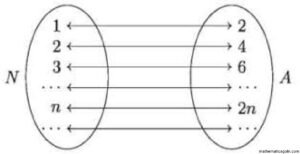
দেখাও যে, স্বাভাবিক সংখ্যার সেট N এবং জোড় সংখ্যার সেট A = {2, 4, 6, …,21. … } সমতুল।
সমাধান:
N = {1,2,3,,, } ও A সমতুল সেট, কারণ N এবং A এর মধ্যে নিচের চিত্রের মতো একটি এক-এক মিল রয়েছে।
চিত্র
মন্তব্য:
উপরে চিত্রিত এক-এক মিলটিকে N = A:n =2n, n∈N দ্বারা বর্ণনা করা যায়। দ্রষ্টব্য: ফাঁকা সেট Ø কে নিজের সমতুল ধরা হয়। অর্থাৎ, Ø ~ Ø
প্রতিজ্ঞা ৪
প্রত্যেক সেট A তার নিজের সমতুল। অর্থাৎ, A ~ A
প্রমাণ:
A = Ø হলে, A ~ A ধরা হয়। আর A ≠ 0 হলে প্রত্যেক সদস্য : এর সঙ্গে তার নিজেকে মিল করে এক-এক মিল A + A E A স্থাপিত হয়। সুতরাং A ~ A
প্রতিজ্ঞা ৫
A ও B সমতুল সেট এবং B ও C সমতুল সেট হলে A ও C সমতুল সেট।
প্রমাণ:
যেহেতু A B, সুতরাং A এর প্রত্যেক সদস্য এর সঙ্গে B এর একটি অনন্য সদস্য এর মিল করা যায়। আবার যেহেতু B ~ C, সুতরাং B এর এই সদস্য y এর সঙ্গে C এর একটি অনন্য সদস্য : এর মিল করা যায়। এখন A এর সদস্য এর সঙ্গে C এর সদস্য এর মিল করা হলে, A ও C সেটের মধ্যে একটি এক-এক মিল স্থাপিত হয়। অর্থাৎ, A ~ C হয়।
ব্যবধি (Interval)
a ও b বাস্তব সংখ্যা এবং a < b হলে
ক) ( a, b ) = ( x ∈ R a <x < b} কে খোলা ব্যবধি (open interval) বলে।
খ) [ a, b ] = [{ x ∈ R a≤ x ≤b} কে বন্ধ ব্যবধি (closed interval) বলে।
গ) (a,b] = {x ∈ R : a < x< b} এবং [a, b) = {x ∈ R : a< x < b} কে যথাক্রমে খোলা-বদ্ধ ও বদ্ধ-খোলা ব্যবধি বলে।

৩ thoughts on “সমতুল সেট”