আজকে আমাদের আলোচনার বিষয়ঃ চতুর্ভুজের প্রকারভেদ । এটি অষ্টম শ্রেনী গণিতের চতুর্ভুজ এর অন্তর্গত।
চতুর্ভুজের প্রকারভেদ (Types of Quadrilaterals)
চতুর্ভুজ (Quadrilateral)
চারটি রেখাংশ দ্বারা আবদ্ধ চিত্র একটি চতুর্ভুজ । চিত্র দ্বারা আবদ্ধ ক্ষেত্রটি একটি চতুর্ভুজক্ষেত্র ।
চতুর্ভুজের চারটি বাহু আছে । যে চারটি রেখাংশ দ্বারা ক্ষেত্রটি আবদ্ধ হয়, এ চারটি রেখাংশই চতুর্ভুজের বাহু ।
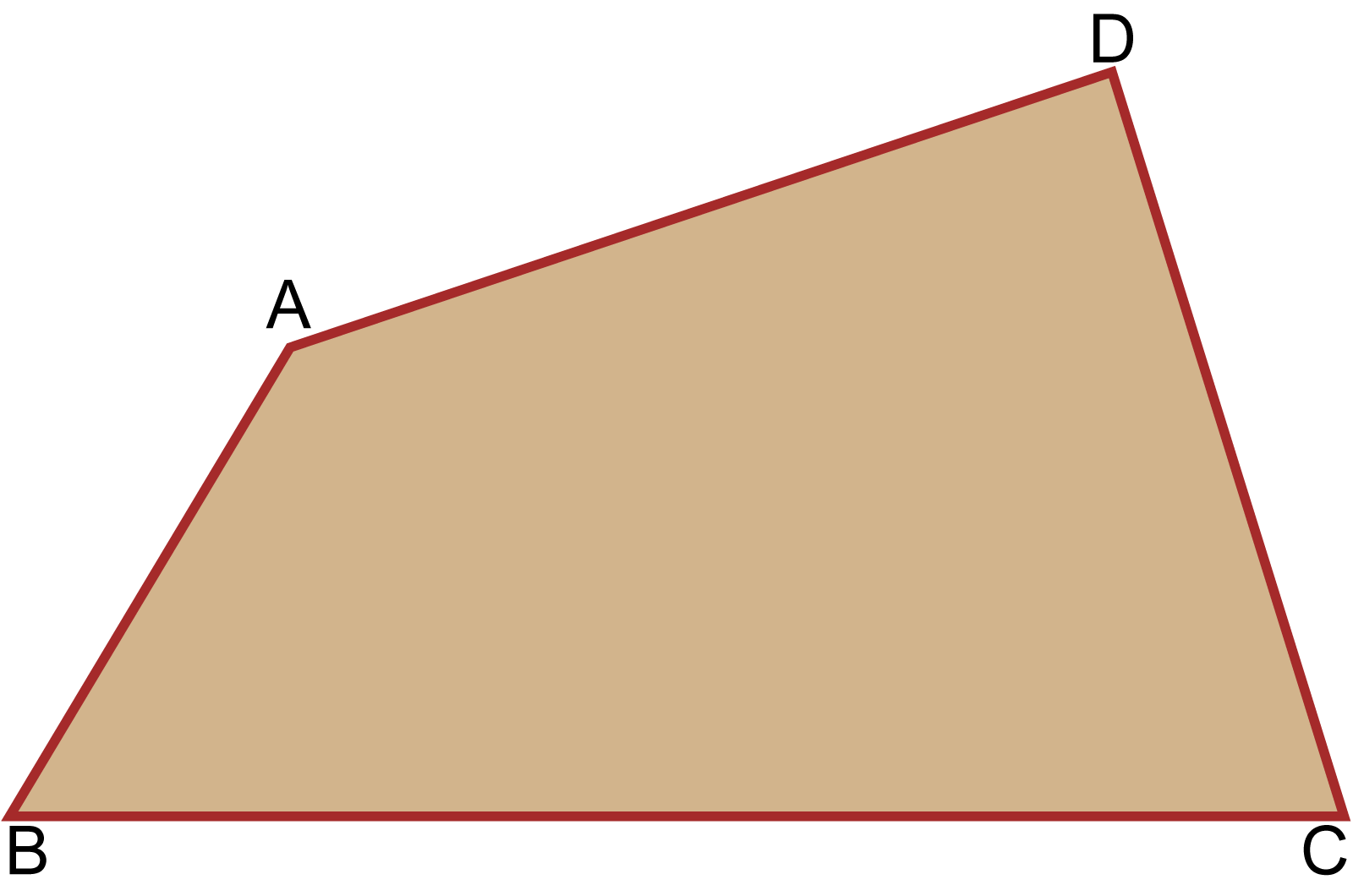
A, B, C ও D বিন্দু চারটির যেকোনো তিনটি সমরেখ নয়। AB, BC, CD ও DA রেখাংশ চারটি সংযোগে ABCD চতুর্ভুজ গঠিত হয়েছে। AB, BC, CD ও DA চতুর্ভুজটির চারটি বাহু । A, B, C ও D চারটি কৌণিক বিন্দু বা শীর্ষবিন্দু। ∠ABC, ∠BCD, ∠CDA ও ∠DAB চতুর্ভুজের চারটি কোণ ।

A ও B শীর্ষবিন্দু যথাক্রমে C ও D শীর্ষের বিপরীত শীর্ষবিন্দু। AB ও CD পরস্পর বিপরীত বাহু এবং AD ও BC পরস্পর বিপরীত বাহু । এক শীর্ষবিন্দুতে যে দুইটি বাহু মিলিত হয়, এরা সন্নিহিত বাহু । যেমন, AB ও BC বাহু দুইটি সন্নিহিত বাহু। AC ও BD রেখাংশদ্বয় ABCD চতুর্ভুজের দুইটি কর্ণ ।
চতুর্ভুজের বাহুগুলোর দৈর্ঘ্যের সমষ্টিকে এর পরিসীমা বলে। ABCD চতুর্ভুজের পরিসীমা (AB + BC + CD + DA) এর দৈর্ঘ্যের সমান । চতুর্ভুজকে অনেক সময় ” প্রতীক দ্বারা নির্দেশ করা হয় ।
চতুর্ভুজের প্রকারভেদ
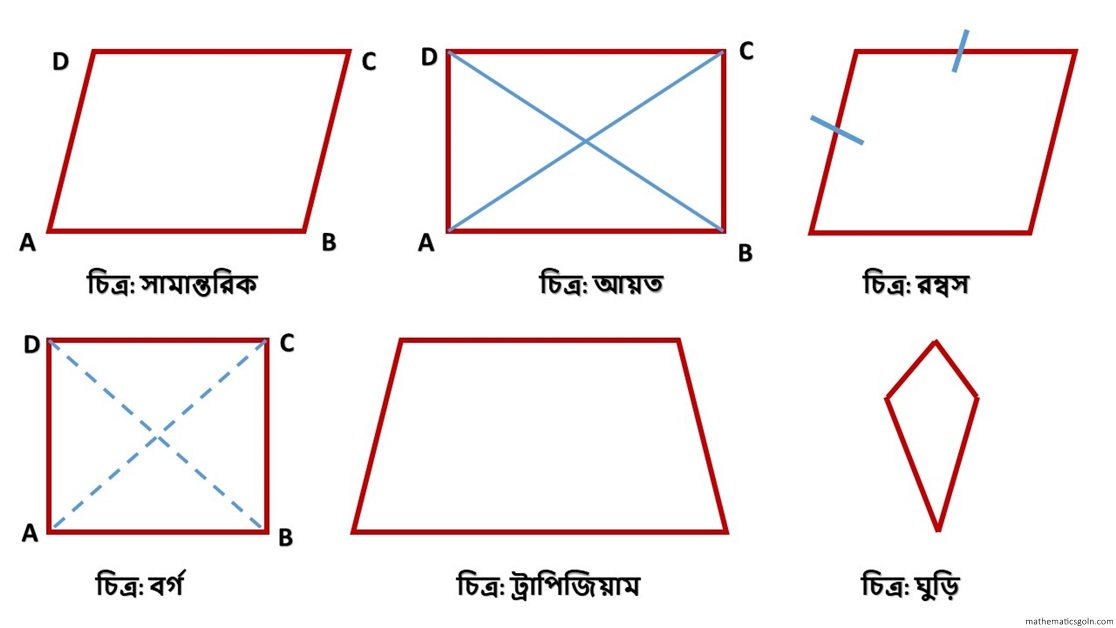
সামান্তরিক :
যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল, তা সামান্তরিক । সামান্তরিকের সীমাবদ্ধ ক্ষেত্রকে সামান্তরিকক্ষেত্র বলে।
আয়ত :
যে সামান্তরিকের একটি কোণ সমকোণ, তাই আয়ত । আয়তের চারটি কোণ সমকোণ । আয়তের সীমাবদ্ধ ক্ষেত্রকে আয়তক্ষেত্র বলে ।
রম্বস :
রম্বস এমন একটি সামান্তরিক যার সন্নিহিত বাহুগুলোর দৈর্ঘ্য সমান। অর্থাৎ, রম্বসের বিপরীত বাহুগুলো সমান্তরাল এবং চারটি বাহু সমান । রম্বসের সীমাবদ্ধ ক্ষেত্রকে রম্বসক্ষেত্র বলে ।
বর্গ :
বর্গ এমন একটি আয়ত যার সন্নিহিত বাহুগুলো সমান । অর্থাৎ, বর্গ এমন একটি সামান্তরিক যার প্রত্যেকটি কোণ সমকোণ এবং বাহুগুলো সমান। বর্গের সীমাবদ্ধ ক্ষেত্রকে বর্গক্ষেত্র বলে ।
ট্রাপিজিয়াম :
যে চতুর্ভুজের এক জোড়া বিপরীত বাহু সমান্তরাল, একে ট্রাপিজিয়াম বলা হয় । ট্রাপিজিয়ামের সীমাবদ্ধ ক্ষেত্রকে ট্রাপিজিয়ামক্ষেত্র বলে ।
ঘুড়ি :
যে চতুর্ভুজের দুই জোড়া সন্নিহিত বাহু সমান, একে ঘুড়ি বলা হয় ।
