আজকে আমরা পিথাগোরাসের উপপাদ্যের অনুশীলনী আলোচনা করবো। এটি অষ্টম শ্রেনী গণিতের পিথাগোরাসের উপপাদ্য এর অন্তর্গত।
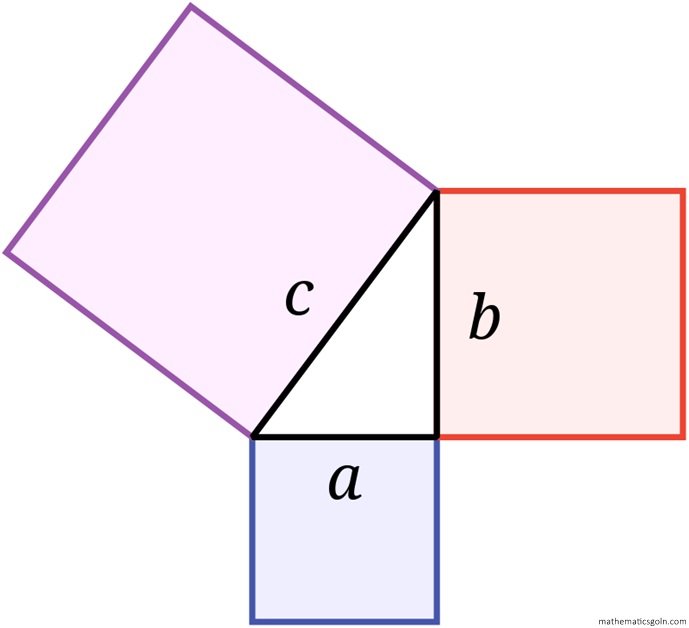
পিথাগোরাসের উপপাদ্যের অনুশীলনী
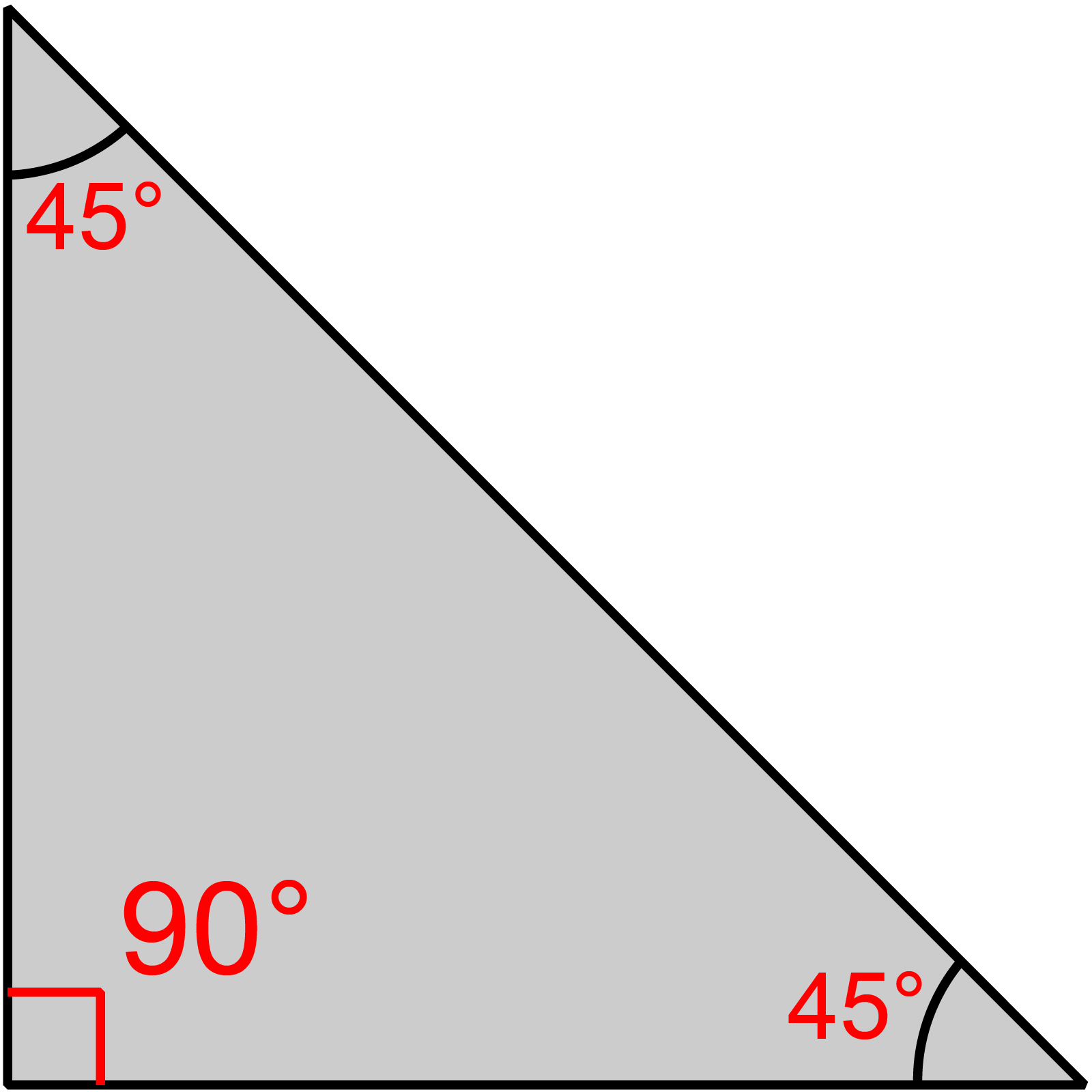
১। একটি ত্রিভুজের বাহুগুলোর অনুপাত 1 : 1 : √2 হলে এর বৃহত্তম কোনটির মান কত ?
ক) 80°
খ) 90°
গ) 100°
ঘ) 120°
২। সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের পার্থক্য 5° হলে ক্ষুদ্রতম কোনটির মান কত?
ক) 40 °
খ) 42.5°
গ) 47.5°
ঘ) 50°
৩। সমকোণী ত্রিভুজের অতিভুজ x একক এবং অপর বাহুদ্বয়ের একটি y একক হলে ৩য় বাহুটির দৈর্ঘ্য কত একক?
ক) x2 + y2
খ) x2 + y2
গ) √(x² – y2)
ঘ) x² – y2
৪। পরিমাপটির কোন পরিমাপের জন্য একটি সমকোণী ত্রিভুজ আঁকা সম্ভব?
ক) 4, 4, 5
খ) 5, 12, 13
গ) 8, 10, 12
ঘ) 2, 3, 4
৫। ∆ABC এ ∠A = ১ সমকোণ হলে এর
i. অতিভুজ BC
i. ক্ষেত্রফল = AB.AC 2
iii.BC2 = AB2 + AC2
নিচের কোনটি সঠিক?
ক) iও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii
৬। সমকোণী ত্রিভুজের-
i. বৃহত্তম বাহুটি অতিভুজ
ii. ক্ষুদ্রতর বাহুদ্বয়ের বর্গের সমষ্টি বৃহত্তম বাহুর বর্গের সমান ।
iii.সূক্ষ্মকোণদ্বয় পরস্পরের পূরক
নিচের কোনটি সঠিক?
নিচের চিত্রের আলোকে ৭-৯ নং প্রশ্নের উত্তর দাও :
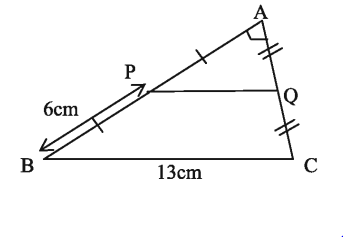
চিত্রে ∠A = 90°
৭। PQ এর দৈর্ঘ্য কত সে.মি.?
ক) 6
খ) 6.5
গ) 7
ঘ) 9.5
৮। ∆ABC = কত বর্গ সে.মি.?
ক) 39
খ) 32.5
গ) 30
ঘ) 15
৯। ∆APQ এর পরিসীমা কত সে.মি.?
ক) 15
খ) 12.5
গ) 10
ঘ) 7.5
ABCDE বহুভুজেAE || BC, CF ⊥ AE এবং DQ ⊥ CF .ED = 10 মি.মি., EF = 2 মি.মি. BC = 8 মি.মি. AB = 12 মি.মি.
উপরের তথ্যের ভিত্তিতে নিচের (১০-১৩) নম্বর প্রশ্নের উত্তর দাও :
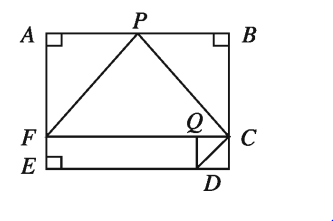
১০। ABCF চতুর্ভুজের ক্ষেত্রফল কত বর্গ মি.মি. ?
ক. 64
খ. 96
গ. 100
ঘ. 144
১১। নিচের কোনটি FPC ত্রিভুজের ক্ষেত্রফল নির্দেশ করে ?
ক. 32 বর্গ মি.মি.
খ. 48 বর্গ মি.মি.
গ. 72 বর্গ মি.মি.
ঘ. 60 বর্গ মি.মি.
১২। CD এর দৈর্ঘ্য নিচের কোনটিতে প্রকাশ পায় ?
ক. 2√2 মি.মি.
খ. 4 মি.মি.
গ. 4√2 মি.মি.
ঘ.৪ মি.মি.
১৩। নিচের কোনটিতে ∆FPC ও ∆DQC এর ক্ষেত্রফলের অন্তর নির্দেশ করে ?
ক. 46 বর্গ মি.মি.
খ. 48 বর্গ মি.মি.
গ. 50 বর্গ মি.মি.
ঘ. 52 বর্গ মি.মি.
১৪। ABC একটি সমবাহু ত্রিভুজ । AD, BC-এর উপর লম্ব ।
প্রমাণ কর যে, AB2 + BC2 + CA2 = 4AD
১৫। ABCD চতুর্ভুজের কর্ণ দুইটি পরস্পরকে লম্বভাবে ছেদ করে ।
প্রমাণ কর যে, AB2 + CD = BC2 + AD 2
১৬। ABC ত্রিভুজের ∠A সমকোণ এবং CD একটি মধ্যমা ।
প্রমাণ কর যে, BC2 = CD 2 + 3AD
১৭। ABC ত্রিভুজের ∠A সমকোণ BP ও CQ দুইটি মধ্যমা ।
প্রমাণ কর যে, 5BC2 = 4 (BP2 + CO2)
১৮। প্রমাণ কর যে, কোনো বর্গক্ষেত্রের কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল ঐ বর্গক্ষেত্রের ক্ষেত্রফলের দ্বিগুণ ।
১৯।
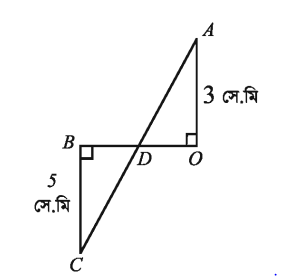
A চিত্রে OB = 4 সে.মি হলে BD এবং AC এর দৈর্ঘ্য নির্ণয় কর ।
২০। প্রমাণ কর যে, কোনো বর্গক্ষেত্র এর কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের অর্ধেক ।
২১। ABC ত্রিভুজের ∠A = এক সমকোণ । D, AC এর উপরস্থ একটি বিন্দু । প্রমাণ কর যে, BC2 + AD2 = BD 2 + AC2
২২। ABC ত্রিভুজের ∠A = এক সমকোণ Dও E যথাক্রমে AB ও AC এর মধ্যবিন্দু হলে, প্রমাণ কর যে, DE2 = CE 2 + BD 2
২৩। ∆ABC এ BC এর উপর লম্ব AD এবং AB > AC প্রমাণ কর যে, AB2 – AC2 = BD 2 – CD2 –
২৪। ∆ABC এ BC এর উপর AD লম্ব এবং AD এর উপর P যেকোনো বিন্দু ও AB > AC প্রমাণ কর যে, PB2 – PC2 = AB2 = AC2
২৫।

ক. POST কী ধরনের চতুর্ভুজ ? স্বপক্ষে যুক্তি দাও ।
খ. দেখাও যে, APRT সমকোণী ।
গ. প্রমাণ কর যে, PR 2 = PQ 2 + QR 2
২৬। ∆PQR এ ∠P = 90°, PQ এবং PR এর মধ্যবিন্দু যথাক্রমে N ও M
ক) ত্রিভুজটি আঁক ।
খ) চিত্র থেকে প্রমাণ কর যে, PR 2 + PQ 2 = QR |
গ) প্রমাণ কর 5RQ2 = 4 (RN2 + QM2 )
