বৃত্তক্ষেত্রের ক্ষেত্রফল

আজকে আমাদের আলোচনার বিষয়ঃ বৃত্তক্ষেত্রের ক্ষেত্রফল । এটি অষ্টম শ্রেনী গণিতের বৃত্তের অন্তর্গত।

 

 

বৃত্তক্ষেত্রের ক্ষেত্রফল

প্রতিদিন আমরা কিছু জিনিস দেখি ও ব্যবহার করি যা বৃত্তাকার : যেমন, গাড়ির চাকা, চুড়ি, ঘড়ি, বোতাম, থালা, মুদ্রা ইত্যাদি । আমরা দেখি যে, ঘড়ির সেকেন্ডের কাঁটার অগ্রভাগ গোলাকার পথে ঘুরতে থাকে । সেকেন্ডের কাঁটার অগ্রভাগ যে পথ চিহ্নিত করে একে বৃত্ত বলে ।

নিখুঁতভাবে বৃত্ত আঁকার জন্য পেন্সিল কম্পাস ব্যবহার করা হয়। কম্পাসের কাঁটাটি কাগজের উপর চেপে ধরে অপর প্রান্তে সংযুক্ত পেন্সিলটি কাগজের উপর চারদিকে ঘুরিয়ে আনলেই একটি বৃত্ত আঁকা হয়ে থাকে, যেমনটি চিত্রে দেখানো হয়েছে । তাহলে বৃত্ত আঁকার সময় নির্দিষ্ট একটি বিন্দু থেকে সমদূরবর্তী বিন্দুগুলোকে আঁকা হয় । এই নির্দিষ্ট বিন্দুটি বৃত্তের কেন্দ্র। কেন্দ্র থেকে সমদূরবর্তী যেকোনো বিন্দুর দূরত্বকে বৃত্তের ব্যাসার্ধ বলা হয় ।

বৃত্ত দ্বারা সীমাবদ্ধ সমতল ক্ষেত্রকে‌ বৃত্তক্ষেত্র বলা হয়। আর বৃত্তটিকে এরূপ বৃত্তক্ষেত্রের সীমারেখা বলা হয়।

বৃত্তক্ষেত্রের ক্ষেত্রফল = আয়তক্ষেত্রটির ক্ষেত্রফল = দৈর্ঘ্য x প্রস্থ

= পরিধির অর্ধেক X ব্যাসার্ধ

= 1/2 x 2πr x r = πr²

বৃত্তক্ষেত্রের ক্ষেত্রফল = πr² বর্গ একক

 

 

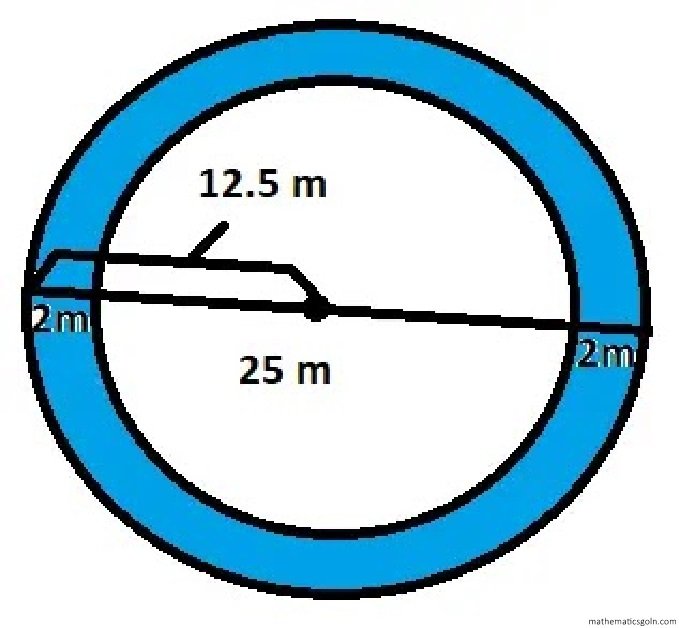
উদাহরণ ৩।

9.8 মি. ব্যাসের বৃত্তাকার একটি বাগানের ক্ষেত্রফল কত?

সমাধান :

বৃত্তাকার বাগানটির ব্যাস, d = 9.8 মি.

বৃত্তাকার বাগানটির ব্যাসার্ধ r = 9.8/2 মি. = 4.9 মি.

বৃত্তাকার বাগানটির ক্ষেত্রফল = πr²

= 3.14 × (4.9)2 বর্গমিটার = 75.39 বর্গমিটার (প্রায়)

 

 

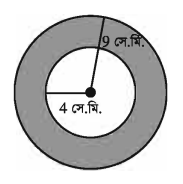
উদাহরণ ৪ ।

পাশের চিত্রে দুইটি সমকেন্দ্রিক বৃত্ত প্রদর্শিত হয়েছে । বৃত্ত দুইটির ব্যাসার্ধ যথাক্রমে 9 সে.মি. ও 4 সে.মি. । বৃত্তদ্বয়ের পরিধির মধ্যবর্তী এলাকার ক্ষেত্রফল কত ?

সমাধান :

বৃহত্তর বৃত্তের ব্যাসার্ধ r = 9 সে.মি.

বৃহত্তর বৃত্তক্ষেত্রটির ক্ষেত্রফল = πr² বর্গ সেন্টিমিটার =  3.14 × (9)2 বর্গ সেন্টিমিটার = 254.34 বর্গ সেন্টিমিটার

ক্ষুদ্রতর বৃত্তের ব্যাসার্ধ r = 4 সে.মি.

ক্ষুদ্রতর বৃত্তক্ষেত্রটির ক্ষেত্রফল = πr² বর্গ সেন্টিমিটার = 3-14 × 42 বর্গ সেন্টিমিটার = 50.24 বর্গ সেন্টিমিটার (প্রায়)

বৃত্তদ্বয়ের মধ্যবর্তী এলাকার ক্ষেত্রফল = (254-34 – 50.24) বর্গ সেন্টিমিটার (প্রায়) = 204-10 বর্গ সেন্টিমিটার (প্রায়)