আজকে আমাদের আলোচনার বিষয়ঃ গাণিতিক গড় । এটি অষ্টম শ্রেনী গণিতের তথ্য ও উপাত্ত এর অন্তর্গত।

গাণিতিক গড় ( Arithmatic Mean)
আমরা জানি, উপাত্তসমূহের সংখ্যাসূচক মানের সমষ্টিকে যদি উপাত্তসমূহের সংখ্যা দিয়ে ভাগ করা হয়, তবে গাণিতিক গড় পাওয়া যায়। মনে করি, উপাত্তসমূহের সংখ্যা n এবং এদের সংখ্যাসূচক মান x1,x2,x3…,xn।
যদি উপাত্তসমূহের গাণিতিক গড় মান X হয়, তবে X = (x1 + x2+x3+…+xn)/n = 1/nΣxi । এখানে, i = Σ [(সিগমা)একটি গ্রিক অক্ষর। যা দ্বারা উপাত্তের সংখ্যাসূচক মানসমূহের যোগফল বোঝানো হয়েছে ।
উদাহরণ ৪ ।
৫০ নম্বরের মধ্যে অনুষ্ঠিত পরীক্ষায় কোনো শ্রেণির ২০ জন শিক্ষার্থীর গণিতের প্রাপ্ত নম্বর ৪০, ৪১, ৪৫, ১৮, ৪১, ২০, ৪৫, ৪১, ৪৫, ২৫, ২০, ৪০, ১৮, ২০, ৪৫, ৪৭, ৪৮, ৪৮, ৪৯, ১৯। প্রাপ্ত নম্বরের গাণিতিক গড় নির্ণয় কর ।
সমাধান :
এখানে n = ২০, x1 = ৪০, x2 = ৪১, x3 = ৪৫,… ইত্যাদি
গাণিতিক গড় যদি x হয়, তবে x= নম্বরগুলোর সমষ্টি /নম্বরগুলোর সংখ্যা
X = 1/nΣxi = (80+8১+8৫+…..+ ১৯)/২০ = ৭১৫/২০ = ৩৫ · ৭৫
গাণিতিক গড় ৩৫.৭৫

অবিন্যস্ত উপাত্তের গাণিতিক গড় নির্ণয় (সংক্ষিপ্ত পদ্ধতি) :
উপাত্তের সংখ্যা যদি বেশি হয় তবে আগের পদ্ধতিতে গড় নির্ণয় করা বেশ জটিল হয় এবং বেশি সংখ্যক উপাত্তের সংখ্যাসূচক মানের সমষ্টি নির্ণয় করতে ভুল হওয়ার সম্ভাবনা থাকে । এক্ষেত্রে সংক্ষিপ্ত পদ্ধতি ব্যবহার করা বেশ সুবিধাজনক ।
সংক্ষিপ্ত পদ্ধতিতে উপাত্তসমূহের কেন্দ্রীয় প্রবণতা ভালোভাবে পর্যবেক্ষণ করে এদের সম্ভাব্য গড় অনুমান করা হয় । উপরের উদাহরণে প্রদত্ত উপাত্তের কেন্দ্রীয় প্রবণতা ভালোভাবে লক্ষ করলে বোঝা যায় যে, গাণিতিক গড় ৩০ থেকে ৪৬ এর মধ্যে একটি সংখ্যা।
মনে করি, গাণিতিক গড় ৩০ । এখন প্রত্যেক সংখ্যা থেকে অনুমিত গড় ৩০ বিয়োগ করে বিয়োগফল নির্ণয় করতে হবে । সংখ্যাটি ৩০ থেকে বড় হলে বিয়োগফল ধনাত্মক এবং ছোট হলে বিয়োগফল ঋণাত্মক হবে । এরপরে সকল বিয়োগফলের বীজগাণিতিক সমষ্টি নির্ণয় করতে হয় । পরপর দুইটি বিয়োগফল যোগ করে ক্রমযোজিত সমষ্টি নির্ণয়ের মাধ্যমে সকল বিয়োগফলের সমষ্টি অতি সহজে নির্ণয় করা যায়। অর্থাৎ, বিয়োগফলের গণসংখ্যা ক্রমযোজিত গণসংখ্যার সমান হবে । উপরের উদাহরণে ব্যবহৃত উপাত্তের গাণিতিক গড় কীভাবে সংক্ষিপ্ত পদ্ধতিতে করা হয় তা নিচের সারণিতে উপস্থাপন করা হলো। মনে করি, উপাত্তসমূহ x (i=1,2,.., n) এর অনুমিত গড় a ( = ৩০)।

|
উপাত্ত,xi |
xi – a |
ক্রমযোজিত গণসংখ্যা |
|
৪০ |
৪০ – ৩০ = ১০ |
১০ |
|
৪১ |
৪১ – ৩০ = ১১ |
১০+১১=২১ |
|
৪৫ |
৪৫ – ৩০ = ১৫ |
২১+১৫=৩৬ |
|
১৮ |
১৮ – ৩০ = -১২ |
৩৬-১২=২৪ |
|
৪১ |
৪১ – ৩০ = ১১ |
২৪+১১=৩৫ |
|
২০ |
২০ – ৩০ = -১০ |
৩৫-১০=২৫ |
|
৪৫ |
৪৫ – ৩০ = ১৫ |
২৫+১৫=৪০ |
|
৪১ |
৪১ – ৩০ = ১১ |
৪০+১১=৫১ |
|
৪৫ |
৪৫ – ৩০ = ১৫ |
৫১+১৫=৬৬ |
|
২৫ |
২৫ – ৩০ = -৫ |
৬৬-৫=৬১ |
|
২০ |
২০ – ৩০ = -১০ |
৬১-১০=৫১ |
|
৪০ |
৪০ – ৩০ = ১০ |
৫১+১০=৬১ |
|
১৮ |
১৮ – ৩০ = -১২ |
৬১-১২=৪৯ |
|
২০ |
২০ – ৩০ = -১০ |
৪৯-১০=৩৯ |
|
৪৫ |
৪৫ – ৩০ = ১৫ |
৩৯+১৫=৫৪ |
|
৪৭ |
৪৭ – ৩০ = ১৭ |
৫৪+১৭=৭১ |
|
৪৮ |
৪৮ – ৩০ = ১৮ |
৭১+১৮=৮৯ |
|
৪৮ |
৪৮ – ৩০ = ১৮ |
৮৯+১৮=১০৭ |
|
৪৯ |
৪৯ – ৩০ = ১৯ |
১০৭+১৯=১২৬ |
|
১৯ |
১৯ – ৩০ = -১১ |
১২৬-১১=১১৫ |
উপরে উপস্থাপিত সারণি থেকে,
ক্রমযোজিত গণসংখ্যা = ১১৫
এবং মোট উপাত্ত সংখ্যা= ২০
… ক্রমযোজিত গণসংখ্যার গড় ১১৫/২০ = ৫.৭৫
সুতরাং প্রকৃত গড়
= অনুমিত গড় + ক্রমযোজিত গণসংখ্যার গড়
= ৩০ + ৫.৭৫ = ৩৫.৭৫
মন্তব্য :
সুবিধার্থে এবং সময় সাশ্রয়ের জন্য কলামের মধ্যকার যোগ-বিয়োগ মনে মনে করে সরাসরি ফলাফল লেখা যায় ।
বিন্যস্ত উপাত্তের গাণিতিক গড়
উদাহরণ ৪ এর ২০ জন শিক্ষার্থীর গণিতে প্রাপ্ত নম্বরের মধ্যে একই নম্বর একাধিক শিক্ষার্থী পেয়েছে ।
প্রাপ্ত নম্বরের গণসংখ্যা নিবেশন সারণি পাশে দেওয়া হলো :
|
প্রাপ্ত নম্বর, xi i = 1,…, k |
গণসংখ্যা,fi i = 1,…, k |
fixi |
|
১৮ |
২ |
৩৬ |
|
১৯ |
১ |
১৯ |
|
২০ |
৩ |
৬০ |
|
২৫ |
১ |
২৫ |
|
৪০ |
২ |
৮০ |
|
৪১ |
৩ |
১২৩ |
|
৪৫ |
৪ |
১৮০ |
|
৪৭ |
১ |
৪৭ |
|
৪৮ |
২ |
৯৬ |
|
৪৯ |
১ |
৪৯ |
|
k = ১০ |
k = ১০, n = ২০ |
মোট = ৭১৫ |
প্রাপ্ত নম্বরের গড় = fixi এর সমষ্টি /মোট গণসংখ্যা = ৭১৫/২০ = ৩৫.৭৫।
সূত্র ১। গাণিতিক গড় (বিন্যস্ত উপাত্ত) :
যদি n সংখ্যক উপাত্তের k সংখ্যক মান x1,x2,x3, …… ,xk
এর গণসংখ্যা যথাক্রমে fi, f2, …, fi হয়, তবে উপাত্তের গাণিতিক গড় =
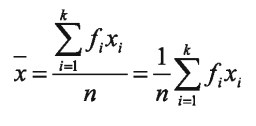
যেখানে n হলো মোট গণসংখ্যা ।
উদাহরণ ৫ ।
নিচে কোনো একটি শ্রেণির ১০০জন শিক্ষার্থীর গণিতে প্রাপ্ত নম্বরের গণসংখ্যা নিবেশন সারণি দেওয়া হলো । প্রাপ্ত নম্বরের গাণিতিক গড় নির্ণয় কর ।
| শ্রেণিব্যাপ্তি |
২৫-৩৪ |
৩৫-৪৪ |
৪৫-৫৪ |
৫৫-৬৪ |
৬৫-৭৪ |
৭৫-৮৪ |
৮৫-৯৪ |
| গণসংখ্যা |
৫ |
১০ |
১৫ |
২০ |
৩০ |
১৬ |
৪ |
সমাধান :
এখানে শ্রেণিব্যাপ্তি দেওয়া আছে বিধায় শিক্ষার্থীদের ব্যক্তিগত নম্বর কত তা জানা যায় না । এ ক্ষেত্রে প্রত্যেক শ্রেণির শ্রেণি মধ্যমান নির্ণয় করার প্রয়োজন হয় ।
শ্রেণি মধ্যমান = (শ্রেণির ঊর্ধ্বমান + শ্রেণির নিম্নমান)/২
যদি শ্রেণি মধ্যমানxi(i = 1,…, k) হয় তবে মধ্যমান সংবলিত সারণি হবে নিম্নরূপ :
|
শ্রেণি ব্যাপ্তি |
শ্রেণি মধ্যমান (xi) |
গণসংখ্যা (fi) |
(fixi) |
|
২৫ – ৩৪ |
২৯.৫ |
৫ |
১৪৭.৫ |
|
৩৫ – ৪৪ |
৩৯.৫ |
১০ |
৩৯৫.০ |
|
৪৫ – ৫৪ |
৪৯.৫ |
১৫ |
৭৪২.৫ |
|
৫৫ – ৬৪ |
৫৯.৫ |
২০ |
১১৯০.০ |
|
৬৫ – ৭৪ |
৬৯.৫ |
৩০ |
২০৮৫.০ |
|
৭৫ – ৮৪ |
৭৯.৫ |
১৬ |
১২৭২.০ |
|
৮৫ – ৯৪ |
৮৯.৫ |
৪ |
৩৫৮.০ |
| মোট | ১০০ |
৬১৯০.০০ |
নির্ণেয় গাণিতিক গড়
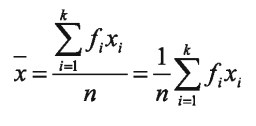
= ১/৬১৯০
= ৬১.৯
