ফাংশনের লেখচিত্র

আজকে আমরা ফাংশনের লেখচিত্র সম্পর্কে  আলোচনা করবো  । যা উচ্চতর গণিতের  সূচকীয় ও লগারিদমীয় ফাংশন অংশের অন্তর্গত।

 

 

ফাংশনের লেখচিত্র

কোনো সমতলে কোনো ফাংশনকে জ্যামিতিকভাবে উপস্থাপন করা গেলে ঐ ফাংশনকে চেনা যায়। ফাংশনের জ্যামিতিকভাবে এই উপস্থাপনকে ফাংশনের লেখচিত্র অঙ্কন করা হয়েছে বলা হয়। এখানে সূচক, লগারিদম ও পরমমান ফাংশনের লেখচিত্রের অঙ্কন পদ্ধতি নিয়ে আলোচনা করা হলো।

(1) y = f(x) = a* এর লেখচিত্র অঙ্কন কর:

(i) যখন a > 1 এবং x যেকোনো ধনাত্মক বা ঋণাত্মক পূর্ণসংখ্যা তখন ফাংশন f(x) = ax সর্বদা ধনাত্মক।

ধাপ ১.

x এর ধনাত্মক মানের জন্য x এর মান বৃদ্ধির সাথে সাথে f(x) এর মান বৃদ্ধি পায়।

ধাপ ২.

যখন x = 0 তখন y = aº = 1, সুতরাং (0, 1) রেখার উপর একটি বিন্দু।

ধাপ ৩.

x এর ঋণাত্মক মানের জন্য x এর মান ক্রমাগত বৃদ্ধির সাথে সাথে f(x) এর মান ক্রমাগত হ্রাস পাবে। অর্থাৎ x → 00 হলে y 0 হবে।

 

 

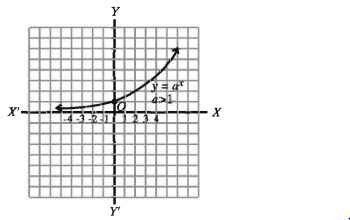
এখানে = yx, a > 1 ফাংশনের লেখচিত্র পাশের চিত্রে দেখানো হলো। এখানে Dj = (-০০, ০০) এবং Rj = (0, 00)।

(ii) যখন 0 <a < 1, x এর মান ধনাত্মক বা ঋণাত্মক তখন ม = f(x) = a* সর্বদাই ধনাত্মক।

ধাপ ১.

লক্ষ করি, মূল বিন্দুর ডানদিকে x এর মান ক্রমাগত বৃদ্ধি পেতে থাকলে অর্থাৎ x 0 হলে y 0 হবে।

ধাপ ২.

যখন = 0 তখন y = a° = 1 সুতরাং ( 0, 1 ) বিন্দু রেখার উপর পড়ে।

 

 

 

ধাপ ৩.

যখন a < 1 এবং ঋণাত্মক তখন x এর মান মূল বিন্দুর বামদিকে ক্রমাগত বৃদ্ধির সাথে সাথে y এর মান ক্রমাগত বৃদ্ধি পাবে অর্থাৎ y = ০০

ধরি a = 1/2 < 1, x < 1, x = −2, −2, −3, ···· –n তখন

y = f(x) = ax = (1/2)−² = 2², y = 2³, …,

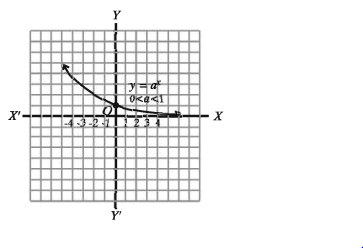
y = 2n. যখন n ⇒ ১০ তখন y + ০০ y f(x) = a” এর লেখচিত্র পাশের চিত্রে দেখানো হলো।

এখানে Dj = (−০০, ০০) এবং R = (0, 00)।

(2) f(x) = logar এর লেখচিত্র অঙ্কন কর:

(i) ধরি, y = f(x) = logax যখন 0 <a < 1। ফাংশনটিকে লেখা যায় x = a

ধাপ ১.

যখন y এর ধনাত্মক মান ক্রমাগত বৃদ্ধি পেতে থাকে অর্থাৎ, y → 00 হয় তখন x এর মান শূন্যের দিকে ধাবিত হয় অর্থাৎ x → 0.

ধাপ ২.

যেহেতু a = 1 কাজেই = সুতরাং রেখাটি (1,0) বিন্দুগামী।

ধাপ ৩.

y এর ঋণাত্মক মান অর্থাৎ y এর মান মূলবিন্দুর নিচের দিকে ক্রমাগত বৃদ্ধি পেতে থাকে অর্থাৎ Y → ০০ হয় তাহলে x এর মান ক্রমাগত বৃদ্ধি পেতে থাকে অর্থাৎ x →00.

 

 

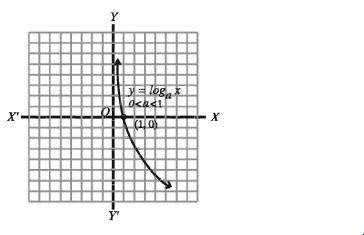
এখন পাশের চিত্রে y = logax, 0 < a < 1 দেখানো হলো। এখানে Df = (0, 0 ) এবং Rf = (- 0,00).

(ii) যখন y = logot, a > 1 তখন

ধাপ ১.

যখন a > 1, y এর সকল মানের জন্য x এর মান ধনাত্মক এবং y এর মানের ক্রমাগত বৃদ্ধির সাথে সাথে x এর মান বৃদ্ধিপ্রাপ্ত হয়। অর্থাৎ y →00 হলে x 00

 

ধাপ ২.

যেহেতু a° = 1 কাজেই =  log1  = 0 সুতরাং, রেখাটি (1,0) বিন্দুগামী।

ধাপ ৩.

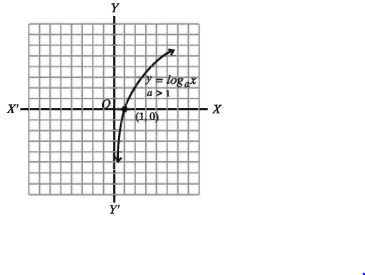
y এর ঋণাত্মক মানের জন্য y এর মান ক্রমাগত বৃদ্ধি পেলে অর্থাৎ, y → 0 হলে x এর মান ক্রমাগত শূন্যের দিকে ধাবিত হয় অর্থাৎ x → 0। এখন f(x) = logar, a > 1 এর লেখচিত্র পাশের চিত্রে দেখানো হলো। এখানে Dj (0, 00) এবং = Rj = (0, 0 )

 

 

উদাহরণ ৩৪.

f(x) = log10* এর লেখচিত্র অঙ্কন কর।

সমাধান:

ধরি y = f(x) = 10810x

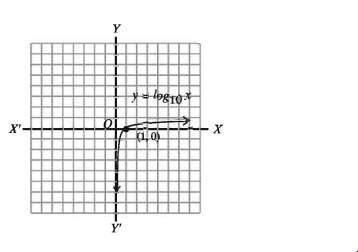
যেহেতু 10° = 1 কাজে‍ই y log 101 = 0 সুতরাং, রেখাটি (1,0) বিন্দুগামী। যখন  → 0 তখন y → 0
যখন → ∞ তখন y ⇒ ∞

:. y = log1ox রেখাটি ঊর্ধ্বগামী।

নিচে রেখাটির লেখচিত্র অঙ্কন করা হলো।

 

 

উদাহরণ ৩৫.

f(x) = Inx এর লেখচিত্র অঙ্কন কর।

সমাধান:

ধরি y = f(x) = ln x

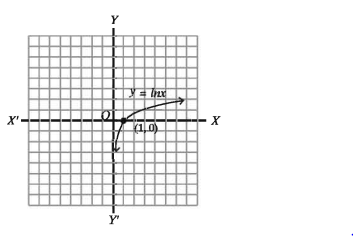
যেহেতু e° = 1 কাজেই y = In1 = 0 সুতরাং, রেখাটি (1,0) বিন্দুগামী। যখন x → 0 তখন y → -∞। যখন x → ∞ তখন y → ∞

.:. y = In x রেখাটি ঊর্ধ্বগামী।

পাশে রেখাটির লেখচিত্র অঙ্কন করা হলো।

এখানে Df= (0, 00) এবং Rf = (- 00, 0 ) ।

 

 

উদাহরণ ৩৬.

y = (4-x)/( 4+ x ) একটি ফাংশন।

ক) ফাংশনটির ডোমেন নির্ণয় কর।

খ) ফাংশনটির বিপরীত ফাংশন নির্ণয় কর।

গ) g ( x ) = In y হলে, g(x) এর ডোমেন নির্ণয় কর।

 

সমাধান :

ক) দেওয়া আছে,  = (4-x)/( 4+ x )

এখানে 4 + x = 0 অর্থাৎ x = − 4 হলে 4 অসংজ্ঞায়িত হয়।

x ≠ − 4

.. ফাংশনটির ডোমেন = R – {4}

খ) দেওয়া আছে,

y = (4-x)/( 4+ x )

ধরি f(x) = y

x = f¹(y)

y = (4-x)/( 4+ x )

4y+xy=4-x

xy+x=4-4y

x(y+1)=4(1 − y)

x = 4(1 − y)/ 1+ y

f¹(y)  = 4(1 − y)/ 1+ y

f¹(x)   = 4(1 − x)/ 1+ x

গ) দেওয়া আছে,

g ( x ) = In (y)

g ( x ) = In(4-x /4+x)

g (x) ∈ R হবে যদি 4 – X/ 4+ x > ০ হয়।

এখন 4-x /4+2 > ০ হবে যদি

(i) 4 – x > 0 এবং 4 + x > 0 হয়, অথবা –

(ii) 4 – x < 0 এবং 4 + x < 0 হয়।

এখন (i) ⇒ x < 4 এবং x > -4

ডোমেন = {x = R : x < 4} ∩ {x € R: x > -4} = (-∞, 4) (-4,∞) = (-4,4)

আবার, (ii) ⇒ x > 4 এবং x < -4

ডোমেন = {x R x > 4}∩ {x R x < -4} = (4,∞)n(−∞, 4) = Ø

প্রদত্ত ফাংশনের ডোমেন = (- 4, 4 ) u = (-4, 4 )