ঘন জ্যামিতির মৌলিক ধারণা

আজকে আমরা ঘন জ্যামিতির মৌলিক ধারণা সম্পর্কে আলোচনা করবো। যা উচ্চতর গণিতের  ঘন জ্যামিতি অংশের অন্তর্গত।

 

 

ঘন জ্যামিতির মৌলিক ধারণা

মাধ্যমিক জ্যামিতিতে বিন্দু, রেখা ও তলের মৌলিক ধারণা আলোচিত হয়েছে। ঘন জ্যামিতিতেও বিন্দু, রেখা ও তলকে মৌলিক ধারণা হিসেবে গ্রহণ করা হয়।

১. বস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা প্রত্যেকটিকে ঐ বস্তুর মাত্রা (dimension) বলা হয়।

২. বিন্দুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা নেই। এটি একটি ধারণা। বাস্তবে বিন্দু বুঝানোর জন্য আমরা একটি ডট (.) ব্যবহার করি। একে অবস্থানের প্রতিরূপ বলা যেতে পারে। সুতরাং বিন্দুর কোনো মাত্রা নেই। তাই বিন্দু শূন্য মাত্রিক।

৩. রেখার কেবল দৈর্ঘ্য আছে, প্রস্থ ও উচ্চতা নেই। তাই রেখা একমাত্রিক। যেমন, নিচের চিত্রে ABI

৪. তলের দৈর্ঘ্য ও প্রস্থ আছে, উচ্চতা নেই। তাই তল দ্বিমাত্রিক। যেমন, নিচের চিত্রে ABGF

৫. যে বস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা আছে, তাকে ঘনবস্তু বলা হয়। সুতরাং ঘনবস্তু ত্রিমাত্রিক। যেমন, নিচের চিত্রে ABCDEFG

 

 

কতিপয় প্রাথমিক সংজ্ঞা

সাধারণত ত্রিমাত্রিক বস্তুর ছবি দ্বিমাত্রিক কাগজ বা বোর্ডে অঙ্কন কিছুটা জটিল। তথাপিও শ্রেণিকক্ষে পাঠদানকালে প্রত্যেকটি সংজ্ঞার ব্যাখ্যার সঙ্গে তার একটি চিত্র অঙ্কন করে দেখিয়ে দিলে বিষয়টি শিক্ষার্থীদের পক্ষে বুঝা ও মনে রাখা সহজতর হবে।

১. সমতল (Plane surface):

কোনো তলের উপরস্থ যেকোনো দুইটি বিন্দুর সংযোজক সরলরেখা সম্পূর্ণরূপে ঐ তলের উপর অবস্থিত হলে, ঐ তলকে সমতল বলা হয়। পুকুরের পানি স্থির থাকলে ঐ পানির উপরিভাগ একটি সমতল। সিমেন্ট দিয়ে নির্মিত বা মোজাইককৃত ঘরের মেঝেকে আমরা সমতল বলে থাকি। কিন্তু জ্যামিতিকভাবে তা সমতল নয়। ঘরের মেঝেতে কিছু উঁচু-নিচু থাকেই। উপরের চিত্রে ABCD, ADEF, ABGF প্রতিটিই এক একটি সমতল।

দ্রষ্টব্য:

অন্য কিছু উল্লেখ না থাকলে ঘন জ্যামিতিতে রেখা বা দৈর্ঘ্য এবং তলের বিস্তার অসীম (infinite) বা অনির্দিষ্ট মনে করা হয়। সুতরাং তলের সংজ্ঞা থেকে অনুমান করা যায় যে, কোনো সরল রেখার একটি অংশ কোনো তলের উপর থাকলে ঐ সরল রেখার অপর কোনো অংশ ঐ তলের বাইরে থাকতে পারে না।

 

 

২. বক্রতল (Curved surface):

কোনো তলের উপর অবস্থিত যে কোনো দুইটি বিন্দুর সংযোজক সরলরেখা সম্পূর্ণরূপে ঐ তলের উপর অবস্থিত না হলে, ঐ তলকে বক্রতল বলা হয়। গোলকের পৃষ্ঠতল একটি বক্রতল ।

৩. ঘন জ্যামিতি (Solid geometry) :

গণিত শাস্ত্রের যে শাখার সাহায্যে ঘনবস্তু এবং তল, রেখা ও বিন্দুর ধর্ম জানা যায়, তাকে ঘন জ্যামিতি (geometry of space) বলা হয়। কখনও কখনও একে জাগতিক জ্যামিতি (geometry of space) বা ত্রিমাত্রিক জ্যামিতিও (geometry of three dimensions) বলা হয়।

৪. একতলীয় রেখা (Coplanar straight lines):

একাধিক সরলরেখা একই সমতলে অবস্থিত হলে, বা তাদের সকলের মধ্য দিয়ে একটি সমতল অঙ্কন সম্ভব হলে ঐ সরলরেখাগুলোকে একতলীয় রেখা বলা হয়। উপরের চিত্রে AB ও CD এক তলীয় রেখা, কিন্তু EF তাদের সাথে একতলীয় নয়।

 

 

৫. নৈকতলীয় রেখা ( Skew or non coplanar lines) :

একাধিক সরলরেখা একই সমতলে অবস্থিত না হলে বা তাদের মধ্য দিয়ে একটি সমতল অঙ্কন করা সম্ভব না হলে এগুলোকে নৈকতলীয় সরলরেখা বলা হয়। উপরের চিত্রে AB ও EF নৈকতলীয় রেখা। দুইটি পেন্সিলকে একটির উপর আর একটি দিয়ে যোগ বা গুণচিহ্ন আকৃতির একটি বস্তু তৈরি করলেই দুইটি নৈকতলীয় সরলরেখা উৎপন্ন হবে।

৬. সমান্তরাল সরলরেখা ( Parallel lines):

দুইটি একতলীয় সরলরেখা যদি পরস্পর ছেদ না করে অর্থাৎ যদি তাদের কোনো সাধারণ বিন্দু না থাকে, তবে তাদের সমান্তরাল সরলরেখা বলা হয়। উপরের চিত্রে AB ও CD সমান্তরাল সরল রেখা।

৭. সমান্তরাল তল (Parallel planes):

দুইটি সমতল যদি পরস্পর ছেদ না করে অর্থাৎ যদি তাদের কোনো সাধারণ রেখা না থাকে তবে ঐ তলদ্বয়কে সমান্তরাল তল বলা হয়। উপরের চিত্রে ABCD ও তার বিপরীত পাশে থাকা EFG সমতল দুটি পরস্পরের সমান্তরাল তল।

৮. সমতলের সমান্তরাল রেখা (Parallel to a plane):

একটি সরলরেখা ও একটি সমতলকে অনির্দিষ্টভাবে বর্ধিত করলেও যদি তারা পরস্পর ছেদ না করে, তবে ঐ সরলরেখাকে উক্ত তলের সমান্তরাল রেখা বলা হয়। উপরের চিত্রে CD সরল রেখা ABGF সমতলের সমান্তরাল রেখা।

৯. তলের লম্ব রেখা (Normal or perpendicular to a plane ) :

কোনো সরলরেখা একটি সমতলের উপরস্থ কোনো বিন্দু থেকে ঐ সমতলের উপর অঙ্কিত যেকোনো রেখার উপর লম্ব হলে, উক্ত সরলরেখাকে ঐ সমতলের উপর লম্ব বলা হয়। নিচের বামের চিত্রে OP রেখা QR সমতলের উপর লম্ব, কারণ OP রেখা QR সমতলে থাকা AB, CD, EF প্রতিটি রেখার ওপরেই লম্ব।

 

 

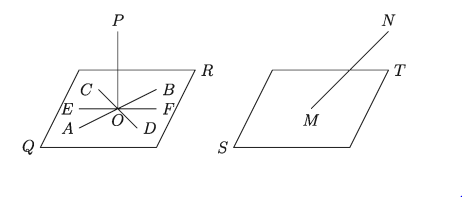
১০. তির্যক (Oblique) রেখা:

কোনো সরলরেখা একটি সমতলের সাথে সমান্তরাল বা লম্ব না হলে, ঐ সরলরেখাকে সমতলের তির্যক রেখা বলা হয়। উপরের ডানের চিত্রে MN, ST এর তির্যক রেখা।

১১. উল্লম্ব (Vertical) রেখা বা তল:

স্থির অবস্থায় ঝুলন্ত ওলনের সুতার সঙ্গে সমান্তরাল কোনো রেখা বা তলকে খাড়া বা উল্লম্ব তল বলে। নিচের বামের চিত্রে ABCD উল্লম্ব তল এবং PR উল্লম্ব রেখা।

 

 

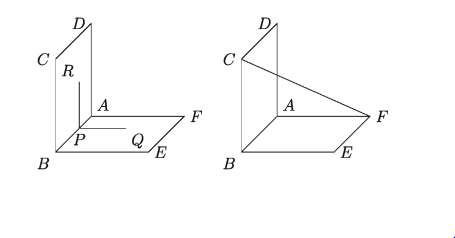
১২. অনুভূমিক (Horizontal) তল ও রেখা:

কোনো সমতল একটি খাড়া সরলরেখার সাথে লম্ব হলে, তাকে শয়ান বা অনুভূমিক তল বলা হয়। আবার কোনো অনুভূমিক তলে অবস্থিত যেকোনো সরলরেখাকে অনুভূমিক সরলরেখা বলা হয়। উপরের বামের চিত্রে ABEF একটি অনুভুমিক সমতল এবং PQ একটি অনুভুমিক সরলরেখা।

১৩. সমতল (Planar) ও নৈকতলীয় (Skew) চতুর্ভুজ:

কোনো চতুর্ভুজের বাহুগুলো সব একই তলে অবস্থিত হলে, তাকে সমতলীয় চতুর্ভুজ বলা হয়। আবার কোনো চতুর্ভুজের বাহুগুলো সকলে একই তলে অবস্থিত না হলে, ঐ চতুর্ভুজকে নৈকতলীয় চতুৰ্ভুজ বলা হয়। নৈকতলীয় চতুর্ভুজের দুইটি সন্নিহিত বাহু একতলে এবং অপর দুইটি অন্য তলে অবস্থিত। সুতরাং কোনো নৈকতলীয় চতুর্ভুজের বিপরীত বাহুদ্বয় নৈকতলীয়। উপরের ডানের চিত্রে ABEF একটি সমতলীয় চতুর্ভুজ এবং BCFE একটি নৈকতলীয় চতুর্ভুজ।

১৪. নৈকতলীয় রেখার (Skew lines) অন্তর্গত কোণ:

দুইটি নৈকতলীয় রেখার অন্তর্গত কোণ তাদের যেকোনো একটি ও তার উপরস্থ কোনো বিন্দু থেকে অঙ্কিত অপরটির সমান্তরাল রেখার অন্তর্গত কোণের সমান। আবার দুইটি নৈকতলীয় রেখার প্রত্যেকের সমান্তরাল দুইটি রেখা কোনো বিন্দুতে অঙ্কন করলে ঐ বিন্দুতে উৎপন্ন কোণের পরিমাণও নৈকতলীয় রেখাদ্বয়ের অন্তর্গত কোণের সমান।

 

 

মনে করি, AB ও CD দুইটি নৈকতলীয় রেখা। যেকোনো O বিন্দুতে AB ও CD এর সমান্তরাল যথাক্রমে OP এবং OQ রেখাদ্বয় অঙ্কন করলে ∠POQ ই AB ও CD এর অন্তর্গত কোণ নির্দেশ করবে। অন্য কথায় ∠BRQ ও AB ও CD এর অন্তর্গত কোণ নির্দেশ করে যেখানে R বিন্দুটি AB এর ওপর অবস্থিত এবং QR তো অবশ্যই CD এর সমান্তরাল।

১৫. দ্বিতল কোণ (Dihedral angle) :

দুইটি সমতল সরলরেখায় ছেদ করলে তাদের ছেদ রেখাস্থ যেকোনো বিন্দু থেকে ঐ সমতলদ্বয়ের প্রত্যেকের উপর ঐ ছেদ রেখার সাথে লম্ব এরূপ একটি করে রেখা অঙ্কন করলে উৎপন্ন কোণই ঐ সমতলদ্বয়ের অন্তর্গত দ্বিতল কোণ।

 

 

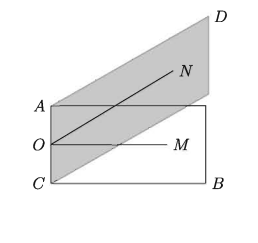
AB ও CD সমতলদ্বয় AC রেখায় পরস্পর ছেদ করেছে। AC রেখাস্থ O বিন্দুতে AB সমতলে OM এবং CD সমতলে ON এরূপ দুইটি সরলরেখা অঙ্কন করা হলো যেন তারা উভয়ই AC এর সঙ্গে O বিন্দুতে লম্ব হয়। তাহলে ZMON ই AB ও CD সমতলদ্বয়ের অন্তর্গত দ্বিতল কোণ সূচিত করে। দুইটি পরস্পচ্ছেদী সমতলের অন্তর্গত দ্বিতল কোণের পরিমাণ এক সমকোণ হলে ঐ সমতলদ্বয় পরস্পর লম্ব।

১৬. অভিক্ষেপ (Projection) :

কোনো বিন্দু থেকে একটি নির্দিষ্ট সরলরেখার উপর বা কোনো সমতলের উপর অঙ্কিত লম্বরেখার পাদবিন্দুকে ঐ রেখা বা সমতলের উপর উক্ত বিন্দুর পাতন বা অভিক্ষেপ (projection) বলা হয়। কোনো সরলরেখা বা বক্ররেখার সকল বিন্দু থেকে কোনো নির্দিষ্ট সমতলের উপর অঙ্কিত লম্বগুলোর পাদবিন্দুসমূহের সেটকে ঐ সমতলের উপর উক্ত সরলরেখা বা বক্ররেখার অভিক্ষেপ বলা হয়। এই অভিক্ষেপকে লম্ব অভিক্ষেপও (orthogonal projection) বলা হয়। চিত্রে XY সমতলের উপর একটি বক্ররেখা AB ও একটি সরলরেখা CD এর অভিক্ষেপ যথাক্রমে বক্ররেখা ab ও সরলরেখা cd দেখানো হয়েছে।

 

 

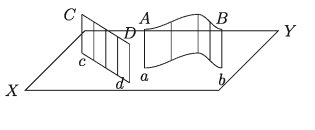
দুইটি সরলরেখার মধ্যে সম্পর্ক

ক) দুইটি সরলরেখা একতলীয় হতে পারে, সেক্ষেত্রে তারা অবশ্যই সমান্তরাল হবে বা কোনো এক বিন্দুতে পরস্পর ছেদ করবে।

খ) দুইটি সরলরেখা নৈকতলীয় হতে পারে, সেক্ষেত্রে তারা সমান্তরালও হবে না কিংবা কোনো বিন্দুতে ছেদও করবে না।

স্বতঃসিদ্ধ

ক) কোনো সমতলের উপরস্থ দুইটি বিন্দুর সংযোজক সরলরেখাকে অনির্দিষ্টভাবে বর্ধিত করলেও তা সম্পুর্ণভাবে ঐ সমতলে অবস্থিত থাকবে। সুতরাং একটি সরলরেখা ও একটি সমতলের মধ্যে দুইটি সাধারণ বিন্দু থাকলে, ঐ সরলরেখা বরাবর তাদের মধ্যে অসংখ্য সাধারণ বিন্দু থাকবে।

খ) দুইটি নির্দিষ্ট বিন্দু বা একটি সরলরেখার মধ্য দিয়ে অসংখ্য সমতল অঙ্কন করা যায়।

সরলরেখা ও সমতলের মধ্যে সম্পর্ক

ক) কোনো সরলরেখা কোনো সমতলের সমান্তরাল হলে তাদের মধ্যে কোনো সাধারণ বিন্দু থাকবে না।

খ) কোনো সরলরেখা কোনো সমতলকে ছেদ করলে তাদের মধ্যে মাত্র একটি সাধারণ বিন্দু থাকবে।

গ) যদি কোনো সরলরেখা ও সমতলের দুইটি সাধারণ বিন্দু থাকে, তাহলে সম্পুর্ণ সরলরেখাটি ঐ সমতলে অবস্থিত হবে।

দুইটি সমতলের মধ্যে সম্পর্ক

ক) দুইটি সমতল পরস্পর সমান্তরাল হলে তাদের মধ্যে কোনো সাধারণ বিন্দু থাকবে না।

খ) দুইটি সমতল পরস্পরছেদী হলে তারা একটি সরলরেখায় ছেদ করবে এবং তাদের অসংখ্য সাধারণ বিন্দু থাকবে।

আরও দেখুনঃ

• স্কেলার রাশি ও ভেক্টর রাশি

• বিভিন্ন প্রকার শর্ট সার্কিট ফল্ট