আজকে আমাদের আলোচনার বিষয়ঃ ত্রিকোণমিতিক অনুপাতের অনুশীলনী ২ । এটি নবম – দশম শ্রেনী গণিতের ত্রিকোণমিতিক অনুপাত এর অন্তর্গত।

ত্রিকোণমিতিক অনুপাতের অনুশীলনী ২
১. cos0 = হলে cot 8 এর মান কোনটি?
ক) 1/√3
খ) 1
গ) √3
ঘ) 2
২. cos20 – sin20 3 = 3 হলে cos48 – sin4৮ এর মান কত?
ক) 3
খ) 2
গ) 1
ঘ) 1/3
৩. cot (0- 30° ) = 1/√3 হলে, sin O 0 = কত?
ক) 1/2
খ) 0
গ) 1
ঘ) √3/2

8. tan ( 3A ) = √3 হলে, A = কত?
ক) 45°
খ) 30°
গ) 20°
ঘ) 15°
৫. 0° < < 90° এর জন্য, sin 8 =এর সর্বোচ্চ মান কত?
ক) – 1
খ) 0
গ) 1/2
ঘ) 1
৬. ABC সমকোণী ত্রিভুজে অতিভুজ AC = 2, AB = 1

(i) ∠ACB = 30°
(ii) tan A = √3
(iii) sin ( A + C ) = 0
নিচের কোনটি সঠিক?
ক) i
খ) ii
গ) i ও ii
ঘ) ii ও iii
৭. ABC সমকোণী ত্রিভুজে অতিভুজ AC = 2, AB = 1
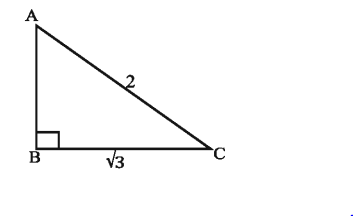
(i) cos A= sin C
(ii) cos A+ sec A =5/2
(iii) tan C =2/√3
নিচের কোনটি সঠিক?
ক) i ও ii
খ) ii ও iii
গ) i ও iii
ঘ) i, ii ও iii
মান নির্ণয় কর ( ৮-১১ )
৮. 1- cot260° /1 + cot260°
৯. tan 45°. sin260°. tan 30°. tan 60°
১০. (1 – cos260°/ 1 + cos260°) + sec²60°
১১. cos 45° cot260°· cosec230°
দেখাও যে, (১২-১৭)
১২. cos230° – sin²30° = cos 60°
১৩. sin 60° cos 30° + cos 60° sin 30° = sin 90°
১৪. cos 60° cos 30° + sin 60° sin 30° = cos 30°
১৫. sin 3A = cos 3A যদি A = 15° হয়।

১৬. sin 2A = 2tan A/( 1+tan2 A) যদি A = 45° হয়।
১৭. tan 2A = 2tan A /(1- tan2 A) = যদি A = 30° হয় ।
১৮. 2cos (A + B) = 1 = 2sin (A – B) এবং A, B সূক্ষ্মকোণ হলে দেখাও যে, A = 45, B = 15°।
১৯. cos (A – B ) = 1 = 2sin (A + B) = √3 এবং A, B সূক্ষ্মকোণ হলে, A এবং B এর মান নির্ণয় কর।
২০. সমাধান কর: cos A – sin A/cos A + sin A = (√3 – 1) /(√3+1)
২১. A ও B সূক্ষ্মকোণ এবং cot (A + B) = 1, cot (A – B) = √3 হলে, A ও B এর মান নির্ণয় কর।
২২. দেখাও যে, cos 3A = 4cos A – 3cos A যদি A = 30° হয়।
২৩. সমাধান কর; sin 0 + cos 0 = 1, যখন 0° ≠ 0 < 90°
২৪. সমাধান কর: cos 20 – sin 20 = 2 – 5cos 8 যখন ৪ সূক্ষ্মকোণ ।
২৫. সমাধান কর: 2sin 20 + 3cos – 3 = 0, 6 সূক্ষ্মকোণ।
২৬. সমাধান কর: tan28 – (1 + √3) tan 6 + √3 = 0

২৭. মান নির্ণয় কর: 3cot2 60° + = 1/4cosec230° + 5sin245° – 4cos 2600
২৮. ∆ABC এর ∠B = 90°, AB = 5 সে.মি., BC = 12 সে.মি.।
ক) AC এর দৈর্ঘ্য নির্ণয় কর।
খ) ∠C = 0 হলে sin 6 + cos 8 এর মান নির্ণয় কর।
গ) উদ্দীপকের আলোকে দেখাও যে, sec2A + cosec2A = sec2A . cosec2A
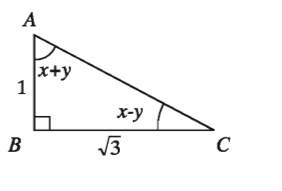
২৯. প্রদত্ত চিত্রের আলোকে
ক) AC এর পরিমাণ কত?
খ) tan A + tan C এর মান নির্ণয় কর।
গ) x ও y এর মান নির্ণয় কর।
30. sini =p, cos0 = q, tan 0 =r, যেখানে ৪ সূক্ষ্মকোণ।
ক) r = (3)-1 হলে ৪ এর মান নির্ণয় কর।
খ) p+ q = √2 হলে প্রমাণ কর যে, 6 = 450
গ) 7p2 + 3q2 = 4 হলে দেখাও যে, tan 6: = 1 √3
৩১. ABC সমকোণী ত্রিভুজের B = এক সমকোণ এবং AB = BC হলে প্রমাণ কর যে, (BCcos C – ACcos B)/(BCcos B-ACcos A) + cos C = 0
৩২. ABC সমকোণী ত্রিভুজের B = এক সমকোণ এবং cot A + cot B = 2cot C হলে প্রমাণ কর যে, AC2 + BC2 = 2AB2
