আজকে আমাদের আলোচনার বিষয়ঃ তিনটি রেখাংশ ত্রিভুজ। এটি নবম – দশম শ্রেনী গণিতের রেখা, কোণ ও ত্রিভুজ এর অন্তর্গত।

তিনটি রেখাংশ ত্রিভুজ
তিনটি রেখাংশ দ্বারা আবদ্ধ চিত্র একটি ত্রিভুজ। রেখাংশগুলোকে ত্রিভুজের বাহু বলে। যেকোনো দুইটি বাহুর সাধারণ বিন্দুকে শীর্ষবিন্দু বলা হয়। ত্রিভুজের যেকোনো দুইটি বাহু শীর্ষবিন্দুতে কোণ উৎপন্ন করে। ত্রিভুজের তিনটি বাহু ও তিনটি কোণ রয়েছে।
বাহুভেদে ত্রিভুজ তিন প্রকার: সমবাহু, সমদ্বিবাহু ও বিষমবাহু।
আবার কোণভেদেও ত্রিভুজ তিন প্রকার: সূক্ষ্মকোণী, স্থূলকোণী ও সমকোণী।
ত্রিভুজের বাহু তিনটির দৈর্ঘ্যের সমষ্টিকে পরিসীমা বলে। ত্রিভুজের বাহুগুলো দ্বারা সীমাবদ্ধ ক্ষেত্রকে ত্রিভুজক্ষেত্র বলে।
ত্রিভুজের যেকোনো শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত অঙ্কিত রেখাংশকে মধ্যমা বলে। আবার, যেকোনো শীর্ষবিন্দু হতে বিপরীত বাহু এর লম্ব দূরত্বই ত্রিভুজের উচ্চতা।
পাশের চিত্রে ABC একটি ত্রিভুজ। A, B, C এর তিনটি শীর্ষবিন্দু। AB, BC, CA এর তিনটি বাহু এবং ∠ABC, ∠BCA, ∠CAB এর তিনটি কোণ। AB, BC, CA বাহুর দৈর্ঘ্যের যোগফল ত্রিভুজটির পরিসীমা।
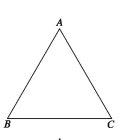
সমবাহু ত্রিভুজ (Equilateral triangle)
যে ত্রিভুজের তিনটি বাহু সমান তা সমবাহু ত্রিভুজ। পাশের চিত্রে ABC ত্রিভুজের AB = BC = CA। অর্থাৎ বাহু তিনটির দৈর্ঘ্য সমান। ABC ত্রিভুজটি একটি সমবাহু ত্রিভুজ।
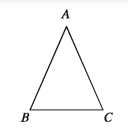
সমদ্বিবাহু ত্রিভুজ (Isosceles triangle )
যে ত্রিভুজের দুইটি বাহু সমান তা সমদ্বিবাহু ত্রিভুজ। পাশের চিত্রে ABC ত্রিভুজের AB = AC ≠ BC। অর্থাৎ দুইটি বাহুর দৈর্ঘ্য সমান, যাদের কোনোটিই তৃতীয় বাহুর সমান নয়। ABC ত্রিভুজটি সমদ্বিবাহু ত্রিভুজ।
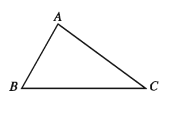
বিষমবাহু ত্রিভুজ (Scalene triangle)
যে ত্রিভুজের তিনটি বাহুই পরস্পর অসমান তা বিষমবাহু ত্রিভুজ। পাশের চিত্রে ABC ত্রিভুজের AB, BC, CA বাহুগুলোর দৈর্ঘ্য পরস্পর অসমান। ABC ত্রিভুজটি বিষমবাহু ত্রিভুজ।

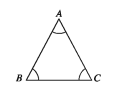
সূক্ষ্মকোণী ত্রিভুজ (Acute triangle)
যে ত্রিভুজের প্রত্যেকটি কোণ সূক্ষ্মকোণ, তা সূক্ষ্মকোণী ত্রিভুজ। ABC ত্রিভুজে ∠BAC, ∠ABC, ∠BCA কোণ তিনটির প্রত্যেকে সূক্ষ্মকোণ। অর্থাৎ প্রত্যেকটি কোণের পরিমাণ 90° অপেক্ষা কম। ∠ABC একটি সূক্ষ্মকোণী ত্রিভুজ।
সমকোণী ত্রিভুজ (Right triangle )
যে ত্রিভুজের একটি কোণ সমকোণ, তা সমকোণী ত্রিভুজ। DEF ত্রিভুজে ∠DFE সমকোণ, অপর কোণ দুইটি ∠DEF ও ∠EDF প্রত্যেকে সূক্ষ্মকোণ। ∆DEF একটি সমকোণী ত্রিভুজ।

স্থূলকোণী ত্রিভুজ (Obtuse triangle)
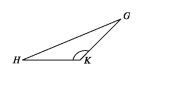
যে ত্রিভুজের একটি কোণ স্থূলকোণ, তা স্থূলকোণী ত্রিভুজ। GHK ত্রিভুজে ∠GKH একটি স্থূলকোণ, অপর কোণ দুইটি ∠GHK ও ∠HGK প্রত্যেকে সূক্ষ্মকোণ। ∆GHK একটি স্থূলকোণী ত্রিভুজ।
ত্রিভুজের বহিঃস্থ ও অন্তঃস্থ কোণ (Exterior angles and interior angles of a triangle)
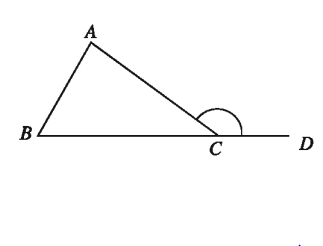
কোনো ত্রিভুজের একটি বাহু বর্ধিত করলে যে কোণ উৎপন্ন হয় তা ত্রিভুজটির একটি বহিঃস্থ কোণ । এই কোণের সন্নিহিত কোণটি ছাড়া ত্রিভুজের অপর দুইটি কোণকে এই বহিঃস্থ কোণের বিপরীত অন্তঃস্থ কোণ বলে।
পাশের চিত্রে, AABC এর BC বাহুকে D পর্যন্ত বর্ধিত করা হয়েছে। ∠ACD ত্রিভুজটির একটি বহিঃস্থ কোণ। ∠ABC, ∠BAC ও ∠ACB ত্রিভুজটির তিনটি অন্তঃস্থ কোণ। ∠ACB কে ∠ACD এর প্রেক্ষিতে সন্নিহিত অন্তঃস্থ কোণ বলা হয় । ∠ABC ও ∠BAC এর প্রত্যেককে ∠ACD এর বিপরীত অন্তঃস্থ কোণ বলা হয়।
উপপাদ্য ৫.
ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান।
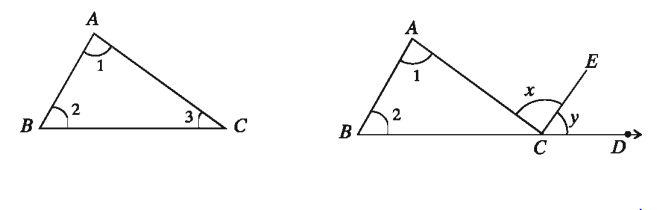
মনে করি, ABC একটি ত্রিভুজ। ত্রিভুজটির ∠BAC + ∠ABC + ∠ACB = দুই সমকোণ
C বিন্দু দিয়ে CE আঁকি যাতে AB || CE হয়। এবার ∠ABC = ∠ECD [অনুরূপ কোণ বলে] এবং ∠BAC = ∠ACE [একান্তর কোণ বলে]
∠ABC + ∠BAC = ∠ECD + ∠ACE = ∠ACD
∠ABC + ∠BAC + ∠ACB = ∠ACD + ∠ACB = দুই সমকোণ
অনুসিদ্ধান্ত ২.
ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।
অনুসিদ্ধান্ত ৩.
ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর অন্তঃস্থ বিপরীত কোণ দুইটির প্রত্যেকটি অপেক্ষা বৃহত্তর।
অনুসিদ্ধান্ত ৪.
সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয় পরস্পর পূরক।
বাহু ও কোণের সর্বসমতা (Congruence of sides and angles)
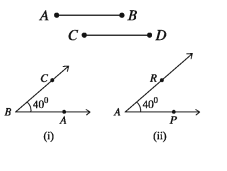
দুইটি রেখাংশের দৈর্ঘ্য সমান হলে রেখাংশ দুইটি সর্বসম। আবার বিপরীতভাবে, দুইটি রেখাংশ সর্বসম হলে এদের দৈর্ঘ্য সমান।
দুইটি কোণের পরিমাপ সমান হলে কোণ দুইটি সর্বসম। আবার বিপরীতভাবে, দুইটি কোণ সর্বসম হলে এদের পরিমাপও B সমান ।
ত্রিভুজের সর্বসমতা (Congruence of triangles )
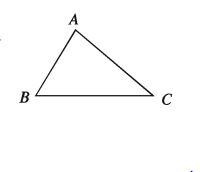
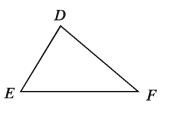
একটি ত্রিভুজকে অপর একটি ত্রিভুজের উপর স্থাপন করলে যদি ত্রিভুজ দুইটি সর্বতোভাবে মিলে যায়, তবে ত্রিভুজ দুইটি সর্বসম হয় । সর্বসম ত্রিভুজের অনুরূপ বাহু ও অনুরূপ কোণগুলো সমান । পাশের চিত্রে ∆ABC ও ∆DEF সর্বসম । ∆ABC ও ∆DEF সর্বসম হলে এবং A, B, C শীর্ষ যথাক্রমে D, E, F শীর্ষের উপর পতিত হলে AB = DE, AC = DF, BC EF এবং ∠A = ∠D, ∠B = ∠E, ∠C = ∠F হবে। ∆ABC ও ∆DEF সর্বসম বোঝাতে ∆ABC = ∆DEF লেখা হয়।
উপপাদ্য ৬. (বাহু-কোণ-বাহু উপপাদ্য)
যদি দুইটি ত্রিভুজের একটির দুই বাহু যথাক্রমে অপরটির দুই বাহুর সমান হয় এবং বাহু দুইটির অন্তর্ভুক্ত কোণ দুইটি পরস্পর সমান হয়, তবে ত্রিভুজ দুইটি সর্বসম।
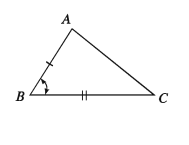
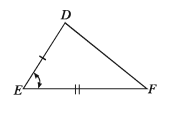
মনে করি, ∆ABC ও ∆DEF এ AB = DE, BC EF এবং অন্তর্ভুক্ত ∠ABC = অন্তর্ভুক্ত ∠DEF তাহলে, ∆ABC = ∆DEF
উপপাদ্য ৭.
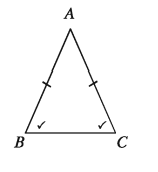
যদি কোনো ত্রিভুজের দুইটি বাহু পরস্পর সমান হয়, তবে এদের বিপরীত কোণ দুইটিও পরস্পর সমান হবে।
মনে করি, ABC ত্রিভুজে AB = AC
তাহলে, ∠ABC = ∠ACB
উপপাদ্য ৮.
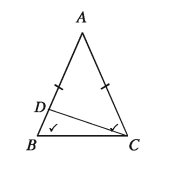
যদি কোনো ত্রিভুজের দুইটি কোণ পরস্পর সমান হয়, তবে এদের বিপরীত বাহু দুইটিও পরস্পর সমান হবে।
বিশেষ নির্বচন
মনে করি, ABC ত্রিভুজে ∠ABC = ∠ACB প্রমাণ করতে হবে যে, AB = AC।
প্ৰমাণ:
ধাপ ১.
যদি AB ≠ AC হয়, তবে (i) AB > AC অথবা (i) AB < AC হবে।
মনে করি, (i) AB > AC AB থেকে AC এর সমান AD কেটে নিই। এখন, ADC ত্রিভুজটি সমদ্বিবাহু। সুতরাং,
∠ADC = ∠ACD [:: সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান]
∆DBC এর বহিঃস্থ কোণ ∠ADC > ∠ABC [ বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণ দুইটির প্রত্যেকটি অপেক্ষা বৃহত্তর]
∠ACD > ∠ABC।
সুতরাং, ∠ACB > ∠ABC, কিন্তু তা প্রদত্ত শর্তবিরোধী।
ধাপ ২.
অনুরূপভাবে, (ii) AB < AC হলে দেখানো যায় যে
∠ABC > ∠ACB, কিন্তু তাও প্রদত্ত শর্তবিরোধী।
ধাপ ৩.
সুতরাং, AB > AC অথবা AB < AC হতে পারে না।
AB = AC (প্রমাণিত)
উপপাদ্য ৯. (বাহু-বাহু-বাহু উপপাদ্য)
যদি একটি ত্রিভুজের তিন বাহু অপর একটি ত্রিভুজের তিন বাহুর সমান হয়, তবে ত্রিভুজ দুইটি সর্বসম হবে।
মনে করি, ∆ABC এবং ∆DEF এ
AB = DE, AC = DF এবং BC = EF
তাহলে, ∆ABC = ∆DEF

উপপাদ্য ১০. (কোণ-বাহু-কোণ উপপাদ্য)
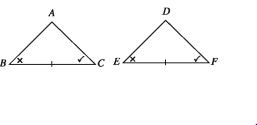
যদি একটি ত্রিভুজের দুইটি কোণ ও এদের সংলগ্ন বাহু যথাক্রমে অপর একটি ত্রিভুজের দুইটি কোণ ও তাদের সংলগ্ন বাহুর সমান হয়, তবে ত্রিভুজ দুইটি সর্বসম হবে।
মনে করি, ∆ABC এবং ∆DEF-এ ∠B = ∠E, ∠C = ∠F এবং কোণদ্বয়ের সংলগ্ন BC বাহু = অনুরূপ EF বাহু। তবে ত্রিভুজ দুইটি সর্বসম, অর্থাৎ ∆ABC = ∆DEF
উপপাদ্য ১১. (অতিভুজ-বাহু উপপাদ্য)
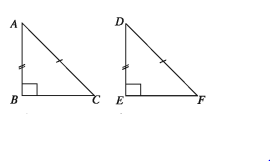
দুইটি সমকোণী ত্রিভুজের অতিভুজদ্বয় সমান হলে এবং একটির এক বাহু অপরটির অপর এক বাহুর সমান হলে, ত্রিভুজদ্বয় সর্বসম।
∆ABC এবং ∆DEF সমকোণী ত্রিভুজদ্বয়ে অতিভুজ AC অতিভুজ DF এবং AB DE। তাহলে, = ∆ABC = ∆DEF
ত্রিভুজের বাহু ও কোণের মধ্যে সম্পর্ক রয়েছে। এ সম্পর্ক নিচের উপপাদ্য ১২ ও উপপাদ্য ১৩ এর প্রতিপাদ্য বিষয়।
উপপাদ্য ১২.
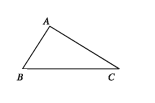
কোনো ত্রিভুজের একটি বাহু অপর একটি বাহু অপেক্ষা বৃহত্তর হলে, বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর।
মনে করি, ∆ABC এ AC > AB।
সুতরাং ∠ABC > ∠ACB
উপপাদ্য ১৩.
কোনো ত্রিভুজের একটি কোণ অপর একটি কোণ অপেক্ষা বৃহত্তর হলে, বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর।
বিশেষ নির্বচন:
মনে করি, ∆ABC এর ∠ABC > ∠ACB প্রমাণ করতে হবে যে, AC > AB

প্ৰমাণ:
ধাপ ১.
যদি AC বাহু AB বাহু অপেক্ষা বৃহত্তর না হয়, তবে (i) AC = AB অথবা (ii) AC < AB হবে।
(i) যদি AC : AB হয়, তবে ∠ABC = ∠ACB [:: সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণদ্বয় সমান]
কিন্তু শর্তানুযায়ী ∠ABC > ∠ACB, তা প্রদত্ত শর্তবিরোধী।
(ii) আবার, যদি AC < AB হয়, তবে ∠ABC < ∠ACB হবে। [ ক্ষুদ্রতর বাহুর বিপরীত কোণ ক্ষুদ্রতর]
কিন্তু তাও প্রদত্ত শর্তবিরোধী।
ধাপ ২.
সুতরাং, AC বাহু AB এর সমান বা AB থেকে ক্ষুদ্রতর হতে পারে না। . AC > AB (প্রমাণিত)।
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টি বা অন্তরের সাথে তৃতীয় বাহুর দৈর্ঘ্যের সম্পর্ক রয়েছে।
উপপাদ্য ১৪.
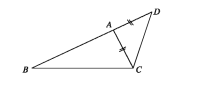
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টি এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর ।
মনে করি, ABC একটি ত্রিভুজ। ধরি, BC ত্রিভুজটির বৃহত্তম বাহু। তাহলে, AB + AC > BC
অনুসিদ্ধান্ত ৫.
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের অন্তর এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা ক্ষুদ্রতর।
মনে করি, ABC একটি ত্রিভুজ। AABC এর যেকোনো দুই বাহুর দৈর্ঘ্যের অন্তর এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা ক্ষুদ্রতর। তাহলে, AB – AC < BC
উপপাদ্য ১৫.
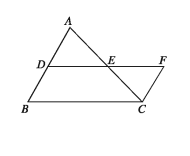
ত্রিভুজের যেকোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল এবং দৈর্ঘ্যে তার অর্ধেক।
বিশেষ নির্বচনঃ
মনে করি, ABC একটি ত্রিভুজ। D ও E যথাক্রমে ত্রিভুজটির AB ও AC বাহুর মধ্যবিন্দু। তাহলে, প্রমাণ করতে হবে যে DE || BC এবং DE = BC
অঙ্কন:
D ও E যোগ করে বর্ধিত করি যেন EF = DE হয়। C, F যোগ করি ।
প্ৰমাণ:
ধাপ ১.
∆ADE ও ∆CEF এর মধ্যে, AE = EC [দেওয়া আছে]
DE = EF [অঙ্কনানুসারে]
অন্তর্ভূক্ত ∠AED = অন্তর্ভূক্ত ∠CEF [বিপ্রতীপ কোণ]
∆ADE = ∆CEF [বাহু-কোণ-বাহু উপপাদ্য ]
∠ADE = ∠EFC [একান্তর কোণ]
AD || CF
আবার, BD = AD = CF এবং BD || CF
সুতরাং BDFC একটি সামান্তরিক।
DF || BC বা DE || BC
ধাপ ২.
আবার, DF = BC বা DE + EF = BC
বা DE + DE = BC বা 2DE = BC বা DE = 1/2BC
DE || BC এবং DE = 1/2BC (প্রমাণিত)।

উপপাদ্য ১৬.
পিথাগোরাসের উপপাদ্য (Pythagorean Theorem) সমকোণী ত্রিভুজের অতিভুজের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর ওপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
মনে করি, ABC সমকোণী ত্রিভুজের ∠ABC সমকোণ এবং AC অতিভুজ। তাহলে, AC2 = AB2 + BC2

উদাহরণ ১.
∆ABC এর AB = AC, BA কে D পর্যন্ত এমনভাবে বর্ধিত করা হল যেন AD = AC হয়। C, D যোগ করা হল ।
ক) উদ্দীপকের ভিত্তিতে চিত্র আঁক।
খ) প্রমাণ কর যে, BC + CD > 2AC
গ) প্রমাণ কর যে, ZBCD = এক সমকোণ।
সমাধান :
ক)
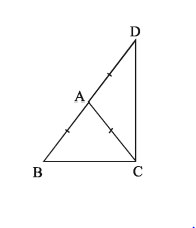
খ) দেওয়া আছে AB = AC এবং অঙ্কন অনুসারে AC = AD
∆BCD এ
BC + CD > BD [ত্রিভুজের যেকোনো দুই বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তর]
বা, BC + CD > AB + AD
বা, BC + CD > AD + AD
বা BC + CD > 2AD
BC + CD > 2AC [ AB = AC = AD]
গ) দেওয়া আছে AB = AC সুতরাং ∠ABC = ∠ACB
অর্থাৎ ∠DBC = ∠ACB
অঙ্কন অনুসারে AC = AD সুতরাং ∠ADC = ∠ACD
অর্থাৎ ∠BDC = ∠ACD
∆BCD এ
∠BDC + ∠DBC + ∠BCD = দুই সমকোণ [ত্রিভুজের তিন কোণের সমষ্টি দুইকোণের সমান
বা, ∠ACD + ∠ACB + ∠BCD = দুই সমকোণ
বা ∠BCD + ∠BCD = দুই সমকোণ
বা, 2∠BCD = দুই সমকোণ।
∠BCD = এক সমকোণ।
উদাহরণ ২.
PQR একটি ত্রিভুজ। PA, QB ও RC তিনটি মধ্যমা O বিন্দুতে ছেদ করেছে।
ক) প্রদত্ত তথ্যের আলোকে চিত্র আঁক।
খ) প্রমাণ কর যে, PQ + PR > QO + RO
গ) প্রমাণ কর যে, PA + QB + RC < PQ + QR + PR
সমাধান :
ক)
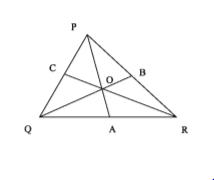
খ) চিত্র ‘ক’ থেকে প্রমাণ করতে হবে যে, PQ + PR > Q0 + RO
প্রমাণ:
ত্রিভুজের যেকোনো দুই বাহুর সমষ্টি তার ৩য় বাহু অপেক্ষা বৃহত্তর
∆PQB এ PQ + PB > QB
আবার ∆BOR এ BR + BO > RO
PQ+PB+ BR + BO > QB+RO
PQ+PR+ BO > QO+OB+RO
PQ+PR>QO+ RO
গ) অঙ্কন :
PA কে D পর্যন্ত বর্ধিত করি যেন PA = AD হয়। Q, D যোগ করি।
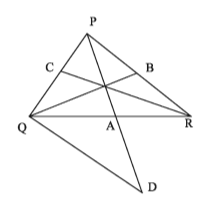
প্ৰমাণ :
∆QAD এবং ∆PAR এ
QA = AR, AD = PA
এবং অন্তর্ভুক্ত ∠QAD = অন্তর্ভুক্ত ∠PAR
∆QAD = ∆PAR এবং QD = PR
এখন ∆PQD এ PQ+QD > PD
বা, PQ+PR>2PA [ A, PD এর মধবিন্দু]
একই ভাবে , PQ+QR > 2QB এবং PR+QR > 2RC
PQ+PR+PQ+QR+PR+QR > 2PA+2QB + 2RC
বা, 2PQ+2QR+2PR > 2PA+2QB + 2RC
বা, PQ+QR+PR > PA+QB + RC
PA+QB + RC < PQ+QR + PR
আরও দেখুনঃ
