আমাদের আজকের আলোচনার বিষয় ভগ্নাংশে ভগ্নাংশে ভাগ – যা ভগ্নাংশের খেলা এর অন্তর্ভুক্ত। গণিত হল জ্ঞানের একটি ক্ষেত্র যাতে সংখ্যা, সূত্র এবং সম্পর্কিত কাঠামো, আকার এবং সেগুলির মধ্যে থাকা স্থানগুলি এবং পরিমাণ এবং তাদের পরিবর্তনগুলি অন্তর্ভুক্ত থাকে। এই বিষয়গুলি যথাক্রমে সংখ্যা তত্ত্বের প্রধান উপশাখা,বীজগণিত, জ্যামিতি, এবং বিশ্লেষণ। তবে একাডেমিক শৃঙ্খলার জন্য একটি সাধারণ সংজ্ঞা সম্পর্কে গণিতবিদদের মধ্যে কোন সাধারণ ঐকমত্য নেই।
গণিতে সংখ্যা ও অন্যান্য পরিমাপযোগ্য রাশিসমূহের মধ্যকার সম্পর্ক বর্ণনা করা হয়। গণিতবিদগন বিশৃঙ্খল ও অসমাধানযুক্ত সমস্যাকে শৃঙ্খলভাবে উপস্থাপনের প্রক্রিয়া খুঁজে বেড়ান ও তা সমাধানে নতুন ধারণা প্রদান করে থাকেন।গাণিতিক প্রমাণের মাধ্যমে এই ধারণাগুলির সত্যতা যাচাই করা হয়। গাণিতিক সমস্যা সমাধান সম্পর্কিত গবেষণায় বছরের পর বছর, যুগের পর যুগ বা শত শত বছর পর্যন্ত লেগে যেতে পারে। গণিতের সার্বজনীন ভাষা ব্যবহার করে বিজ্ঞানীরা একে অপরের সাথে ধারণার আদান-প্রদান করেন। গণিত তাই বিজ্ঞানের ভাষা।
ভগ্নাংশে ভগ্নাংশে ভাগ
ঘরের দেয়াল রঙ করার জন্য তোমাদের বাড়িতে নীল রঙ কিনে আনা হলো। রঙটির ২ ডেসি লিটার দ্বারা ১৮/৫ বর্গ মি. দেয়াল রঙ করা যায়। ১ ডেসি লিটার রঙ দ্বারা ঐ দেয়ালের কত অংশ রঙিন করা যাবে?
প্রথমে সংখ্যা রেখার সাহায্যে সমস্যাটিকে গাণিতিক বাক্যের মাধ্যমে প্রকাশ করি।

মোট রঙিন দেয়ালের ক্ষেত্রফল ÷ রঙ এর পরিমাণ = ১ ডেসি লিটার রঙ দ্বারা রঙিন দেয়ালের ক্ষেএফল
চলো হিসাব করি: ১৮/৫ ÷ ২ = ১৮/৫ × = ?

এবার আরেকটা সমস্যা সমাধান করি।
৩/৫ বর্গমিটার দেয়াল রঙিন করতে ১/৩ ডেসি লিটার রং লাগে। ১ ডেসি লিটার রং দ্বারা ঐ জায়গাটির কত বর্গমিটার দেয়াল রঙিন করা যাবে?
মোট রঙিন দেয়ালের ক্ষেত্রফল ÷ রঙ এর পরিমাণ = ১ ডেসি লিটার রঙ দ্বারা রঙিন দেয়ালের ক্ষেএফল

চিত্র ব্যবহার করে ৩/৫ ÷ ১/৩ কীভাবে হিসাব করা যায় তা চিন্তা করি।
আমরা ১ ডেসি লিটার রং দ্বারা রঙিন অংশের ক্ষেত্রফল নির্ণয় করব।
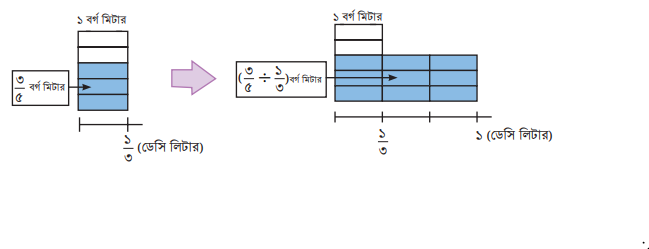
১ ডেসি লিটার হলো ১/৩ ডেসি লিটার এর ৩ গুণ।
১/৩ ডেসি লিটার রং দ্বারা যতটুকু অংশ রঙিন করা যায় তার ৩। গুণ রং করা যাবে ১ ডেসি লিটার রং দ্বারা।

বিপরীত ভগ্নাংশের মাধ্যমে:
ভাজ্য ও ভাজককে একই সংখ্যা দিয়ে গুণ অথবা ভাগ করলে ভাগফলের কোনো পরিবর্তন হয় না।
যেমন: ৬+২=৩ তাহলে, (৬০৫)÷(২×৫)=৩০÷১০=৩
আবার, (৬+২)÷(২+২)=৩+১=৩
ভগ্নাংশের ক্ষেত্রেও সমতুল ভগ্নাংশ নির্ণয়ে আমরা লব ও হরকে একই সংখ্যা দিয়ে গুণ অথবা ভাগ করে থাকি। দুটি ভগ্নাংশের ভাগের ক্ষেত্রেও আমরা একই ধারণা ব্যবহার করতে পারি।
ভগ্নাংশকে পূর্ণসংখ্যা দিয়ে গুণ ও ভাগের ধারণা এবং বিপরীত ভগ্নাংশের মাধ্যমে চাইলে আরও বেশ কিছু উপায়ে দুইটি ভগ্নাংশের ভাগ করা যায়।
আরও দেখুনঃ
