ভেক্টরের সমতা ও বিপরীত ভেক্টর 

আজকে আমরা ভেক্টরের সমতা ও বিপরীত ভেক্টর  আলোচনা করবো। যা উচ্চতর গণিতের  সমতলীয় ভেক্টর অংশের অন্তর্গত।

 

 

ভেক্টরের সমতা ও বিপরীত ভেক্টর

সমান ভেক্টর:

সমজাতীয় দুটি ভেক্টরের মান যদি সমান হয় আর তাদের দিক যদি একই দিকে হয় তবে তাদেরকে সমান ভেক্টর বলে।

একটি ভেক্টর u কে অপর একটি ভেক্টর v এর সমান বলা হয় যদি

ক) |u| = |v| (u এর দৈর্ঘ্য v এর দৈর্ঘ্যের সমান)

খ) u এর ধারক, v এর ধারকের সঙ্গে অভিন্ন অথবা সমান্তরাল হয়

গ) u এর দিক v এর দিকের সঙ্গে একই মুখী হয়।

 

 

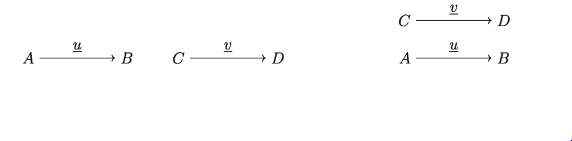
সমতার এই সংজ্ঞা যে নিচের নিয়মগুলো মেনে চলে, তা সহজেই বুঝা যায়:

ক) u = u

খ) u = v হলে v = u

গ) u = v এবং v = w হলে u = w

u এর ধারক এবং v এর ধারক রেখাদ্বয় অভিন্ন বা সমান্তরাল হলে, আমরা সংক্ষেপে বলব u এবং v সমান্তরাল ভেক্টর।

 

 

দ্রষ্টব্য:

যেকোনো বিন্দু থেকে প্রদত্ত যেকোনো ভেক্টরের সমান করে একটি ভেক্টর টানা যায়। কেননা, বিন্দু P এবং ভেক্টর u দেওয়া থাকলে, আমরা P বিন্দু দিয়ে u এর ধারকের সমান্তরাল করে একটি সরলরেখা টানি, তারপর P বিন্দু থেকে u এর দিক বরাবর |u| এর সমান করে PQ রেখাংশ কেটে নিই। তাহলে অঙ্কন অনুযায়ী PQ = u হয়।

বিপরীত ভেক্টর:

নির্দিষ্ট দিক বরাবর কোনো ভেক্টরকে ধনাত্মক ধরলে তার বিপরীত দিকে সমমানের সমজাতীয় ভেক্টরকে ঋণাত্মক ভেক্টর বা বিপরীত ভেক্টর বলে।

 

 

v কে u এর বিপরীত ভেক্টর বলা হয়, যদি

ক) |v| = |u|

খ) v এর ধারক, u এর ধারকের সঙ্গে অভিন্ন বা সমান্তরাল হয়

গ) v এর দিক u এর দিকের বিপরীত হয়।

v যদি u এর বিপরীত ভেক্টর হয়, তবে u  হবে v এর বিপরীত ভেক্টর। সমতার সংজ্ঞা থেকে বুঝা যায় যে, v এবং w প্রত্যেকে u এর বিপরীত ভেক্টর হলে y = w হয়। u এর বিপরীত ভেক্টর বুঝাতে -u লেখা হয়। u = AB হলে – u = BA

 

বিপরীত ভেক্টর নিয়ে বিস্তারিত ঃ

 

আরও দেখুনঃ

• স্কেলার রাশি ও ভেক্টর রাশি