দূরত্ব ও উচ্চতা

আজকে আমাদের আলোচনার বিষয়ঃ দূরত্ব ও উচ্চতা ।  এটি নবম – দশম শ্রেনী গণিতের দূরত্ব ও উচ্চতা এর অন্তর্গত।

 

 

দূরত্ব ও উচ্চতা

ভূ-রেখা, ঊর্ধ্বরেখা এবং উল্লম্বতল (Horizontal Line, Vertical Line and Vertical Plane)

ভূ-রেখা হচ্ছে ভূমি তলে অবস্থিত যে কোনো সরলরেখা। ভূ-রেখাকে শয়নরেখাও বলা হয়। ঊর্ধ্বরেখা হচ্ছে ভূমি তলের উপর লম্ব যে কোনো সরলরেখা। একে উল্লম্ব রেখাও বলে।

ভূমি তলের উপর লম্বভাবে অবস্থিত পরস্পরচ্ছেদী ভূ-রেখা ও ঊর্ধ্বরেখা একটি তল নির্দিষ্ট করে। এ তলকে উল্লম্ব তল বলে।

চিত্রে ভূমি তলের কোনো স্থান C থেকে CB দূরত্বে AB উচ্চতা বিশিষ্ট একটি গাছ লম্ব অবস্থায় দন্ডায়মান। এখানে CB রেখা হচ্ছে ভূ-রেখা, BA রেখা হচ্ছে ঊর্ধ্বরেখা এবং ABC তলটি ভূমির উপর লম্ব যা উল্লম্বতল।

 

 

উন্নতি কোণ ও অবনতি কোণ (Angle of Elevation and Angle of Depression )

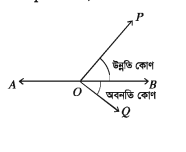
চিত্রটি লক্ষ করি, ভূমির সমান্তরাল AB একটি সরলরেখা। A, O, B, P, Q বিন্দুগুলো একই উল্লম্বতলে অবস্থিত। AB সরলরেখার উপরের P বিন্দুটি AB রেখার সাথে ∠POB উৎপন্ন করে। এখানে, O বিন্দুর সাপেক্ষে P বিন্দুর উন্নতি কোণ ∠POB।

সুতরাং ভূতলের উপরের কোন বিন্দু ভূমির সমান্তরাল রেখার সাথে যে কোণ উৎপন্ন করে তাকে উন্নতি কোণ বলা হয়।

Q বিন্দু ভূ-রেখার সমান্তরাল AB রেখার নিচের দিকে অবস্থিত। এখানে, O বিন্দুর সাপেক্ষে Q বিন্দুর অবনতি কোণ হচ্ছে ZQOB সুতরাং ভূতলের সমান্তরাল রেখার নিচের কোন বিন্দু ভূ-রেখার সাথে যে কোণ উৎপন্ন করে তাকে অবনতি কোণ বলা হয় ।

 

 

বিশেষ দ্রষ্টব্য:

এ অধ্যারে সমস্যা সমাধানের ক্ষেত্রে আনুমানিক সঠিক চিত্র আবশ্যক। চিত্র অঙ্কনের সময় নিচের কৌশল অবলম্বন করা দরকার।

 

 

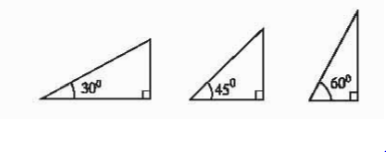
১. 30° কোণ অঙ্কনের ক্ষেত্রে ভূমি > লম্ব হবে।

২. 45° কোণ অঙ্কনের ক্ষেত্রে ভূমি = লম্ব হবে।

৩. 60° কোণ অঙ্কনের ক্ষেত্রে ভূমি < লম্ব হবে।

উদাহরণ ১.

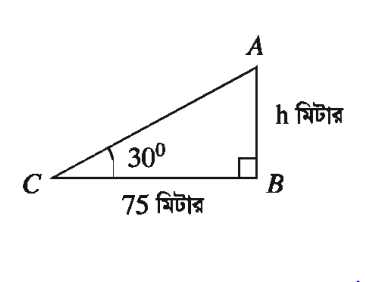
একটি টাওয়ারের পাদদেশ থেকে 75 মিটার দূরে ভূতলস্থ কোনো বিন্দুতে টাওয়ারের শীর্ষের উন্নতি 30° হলে, টাওয়ারের উচ্চতা নির্ণয় কর।

সমাধান:

মনে করি, টাওয়ারের উচ্চতা AB = / মিটার, টাওয়ারের পাদদেশ থেকে BC = 75 মিটার দূরে ভূতলম্ব C বিন্দুতে টাওয়ারের শীর্ষ A বিন্দুর উন্নতি ∠ACB = 30°

সমকোণী ∆ABC থেকে পাই, tan∠ACB = AB/BC

বা, tan 30° বা, = h/75 বা, 1/√3 = h/75  বা, √3h = 75 বা, h = 75/√3

বা, h = 75√3/3  [হর এবং লবকে √3 দ্বারা গুণ করে ]

বা, h = 25√3

h = 43.301 (প্রায়)।

টাওয়ারের উচ্চতা 43.30 মিটার (প্রায়)।

 

 

উদাহরণ ২.

একটি গাছের উচ্চতা 105 মিটার। গাছটির শীর্ষ ভূমির কোনো বিন্দুতে উন্নতি কোণ 60° তৈরি করলে, গাছটির গোড়া থেকে ভূতলস্থ বিন্দুটির দূরত্ব নির্ণয় কর।

সমাধান :

মনে করি, গাছের গোড়া থেকে ভূতলস্থ বিন্দুটির দূরত্ব BC = x মিটার, গাছের উচ্চতা AB 105 মিটার এবং C বিন্দুতে গাছটির শীর্ষ A বিন্দুর উন্নতি ∠ACB = 60°

 

 

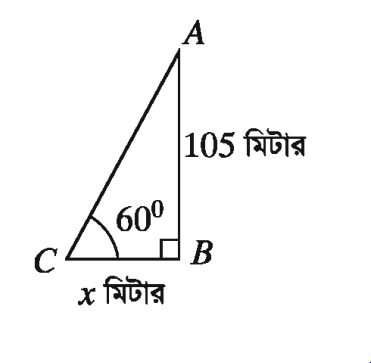
সমকোণী ∆ABC থেকে পাই, tan∠ACB = AB/BC

বা, tan 60° = 105/

বা, √3 = 105/x  [‘. tan 60° = √3]

বা, √3x = 105

বা, x = 105/√3

বা, x = 105/√3/3

বা, x = 35/3

x = 60.622 (প্রায়)

গাছটির গোড়া থেকে ভূতলস্থ বিন্দুটির দূরত্ব 60.62 মিটার (প্রায়)।

উদাহরণ ৩.

18 মিটার লম্বা একটি মই একটি দেওয়ালের ছাদ বরাবর ঠেস দিয়ে ভূমির সঙ্গে 45° কোণ উৎপন্ন করে। দেওয়ালটির উচ্চতা নির্ণয় কর।

সমাধান:

মনে করি, দেওয়ালটির উচ্চতা AB = h মিটার, মইটির দৈর্ঘ্য AC = 18 মিটার এবং ভূমির সঙ্গে LACB = 45° উৎপন্ন করে।

 

 

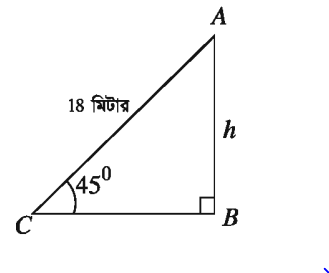
∆ABC থেকে পাই, sin ∠ACB

বা, sin 45° = h/18

বা, 1/√2 = h/18

বা, √2h = 18

বা, h = 18√2

বা, h = 18√2/2  [হর এবং লবকে √2 দ্বারা গুণ করে ]

বা, h = 12.728 (প্রায়)

সুতরাং দেওয়ালটির উচ্চতা 12.73 মিটার (প্রায়)।

উদাহরণ ৪.

ঝড়ে একটি গাছ হেলে পড়লো। গাছের গোড়া থেকে 7 মিটার উচ্চতায় একটি খুঁটি ঠেস দিয়ে গাছটিকে সোজা করা হলো। মাটিতে খুঁটিটির স্পর্শ বিন্দুর অবনতি কোণ 30° হলে, খুঁটিটির দৈর্ঘ্য নির্ণয় কর।

সমাধান:

মনে করি, খুঁটিটির দৈর্ঘ্য BC = 2 মিটার, গাছের গোড়া থেকে AB = 7 মিটার উচ্চতায় খুঁটিটি ঠেস দিয়ে আছে এবং অবনতি ∠DBC = 30°

 

 

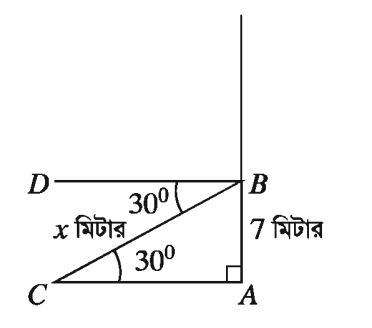
∠ACB = ∠DBC = 30° [একান্তর কোণ বলে]

সমকোণী ∆ABC থেকে পাই,

sin ∠ACB = AB/BC

বা, sin 30° = 7/ BC

বা, 1/2 = 7/ BC

BC = 14

খুঁটিটির দৈর্ঘ্য 14 মিটার।

উদাহরণ ৫.

ভূতলস্থ কোনো স্থানে একটি দালানের ছাদের একটি বিন্দুর উন্নতি কোণ 60°। ঐ স্থান থেকে 42 মিটার পিছিয়ে গেলে দালানের ঐ বিন্দুর উন্নতি কোণ 45° হয়। দালানের উচ্চতা নির্ণয় কর।

সমাধান:

মনে করি, দালানের উচ্চতা AB = h মিটার এবং শীর্ষের উন্নতি ∠ACB = 60° এবং C স্থান থেকে CD = 42 মিটার পিছিয়ে গেলে উন্নতি ∠ADB = 45° হয়।

 

 

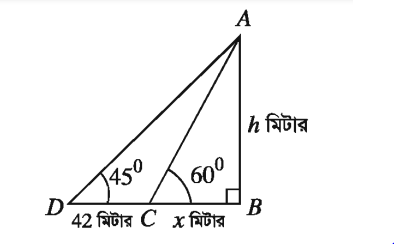
ধরি, BC = X মিটার ।

BD = BC + CD = (x + 42) মিটার।

∆ABC থেকে পাই,

tan ∠ACB = AB/BC

বা, tan 60° = h/x

বা, √3 = h/x [:: tan 60° = √3]

বা, x= h/√3 ……(1)

আবার, ∆ABD থেকে পাই, tan ∠ADB = tan 45° = AB/BD

বা, tan 45° = h/( x +42)

বা, 1 = h/(x+42) [ tan 45° = 1]

বা, h = x + 42 বা,  h = h/√3 + 42 [(1) নং সমীকরণের সাহায্যে ]

বা, √3h = h + 42√3 বা, √3h – h = 42√3 বা, (√3 – 1 ) h = 42√3 বা, h = 42√3/(√3-1)

.: h = 99.373 (প্রায়)

.: দালানটির উচ্চতা 99.37 মিটার (প্রায়)।

উদাহরণ ৬.

একটি খুঁটি এমন ভাবে ভেঙে গেল যে, তার অবিচ্ছিন্ন ভাঙা অংশ দন্ডায়মান অংশের সাথে 30° কোণ উৎপন্ন করে খুঁটির গোড়া থেকে 10 মিটার দূরে মাটি স্পর্শ করে। খুঁটির সম্পূর্ণ দৈর্ঘ্য নির্ণয় কর।

সমাধান:

মনে করি, খুঁটির সম্পূর্ণ দৈর্ঘ্য AB = h মিটার, খুঁটিটি BC = X মিটার উচ্চতায় ভেঙে গিয়ে বিচ্ছিন্ন না হয়ে ভাঙা অংশ দণ্ডায়মান অংশের সাথে ∠BCD = 30° উৎপন্ন করে খুঁটির গোড়া থেকে BD = 10 মিটার দূরে মাটি স্পর্শ করে।

 

 

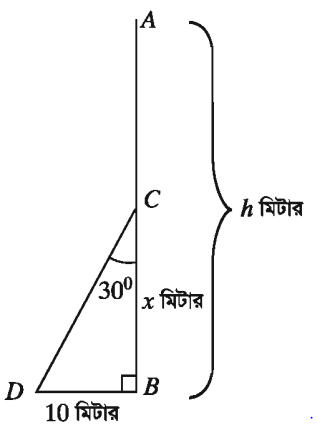
এখানে, CD = AC = AB – BC = (h – x ) মিটার

∆BCD থেকে পাই,

tan ∠BCD = BD/BC

বা, tan 30° = 10/x

বা, 1/√3 =10/x

x = 10√3

আবার, sin ∠BCD = BD/CD

বা, sin 30° =  BD/CD

বা,  1/2 = 10/(h – x)

বা, h – x = 20

বা, h = 20 + x

বা, h = 20 + 10√3 [ x এর মান বসিয়ে]

h = 37.321 (প্রায়)

খুঁটির দৈর্ঘ্য 37.32 মিটার (প্রায়)।